Формула Тейлора с остаточным членом в форме Лагранжа
Пусть функция  n раз непрерывно дифференцируема на n раз непрерывно дифференцируема на  (т. е. (т. е.  и эта функция непрерывна и эта функция непрерывна  ) и имеет в каждой точке этого интервала, за исключением, быть может, точки ) и имеет в каждой точке этого интервала, за исключением, быть может, точки 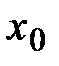 производную производную  - го порядка. Тогда для любого - го порядка. Тогда для любого  между между 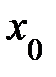 и х найдется такая точка и х найдется такая точка  , что справедлива формула Тейлора , что справедлива формула Тейлора
 ... ...  , (4.20) , (4.20)
где  – остаточный член в форме Лагранжа. Так как точка – остаточный член в форме Лагранжа. Так как точка  , то , то  , где , где 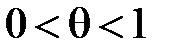 . .
Формула (4.20) является количественной характеристикой погрешности.
Формула Маклорена[11]
Формулой Маклорена называется формула Тейлора при  : :
 ... ... 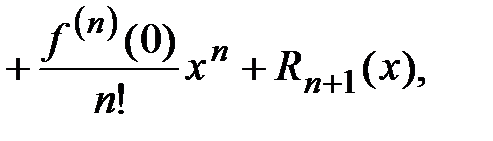
где
 , ,  . .
Пример 4.12.Разложить функцию  по степеням по степеням  . .
Решение.  , , 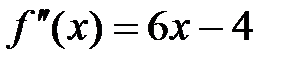 , ,  , ,  . Отсюда . Отсюда
  . .
Следовательно, по формуле Тейлора третьего порядка
 . .
Остаточный член  . Таким образом, . Таким образом,
 . .
Пример 4.13.Разложить функцию  по формуле Тейлора в окрестности точки по формуле Тейлора в окрестности точки  . .
Имеем  , , 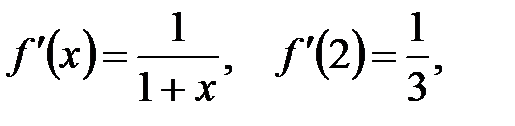

 … , … ,

 где 2 < x < x. где 2 < x < x.
Поэтому 

где  , ,   . .
Разложения основных элементарных функций (асимптотические формулы)
Запишем формулу Тейлора (4.19) при  с остаточным членом в форме Пеано: с остаточным членом в форме Пеано:
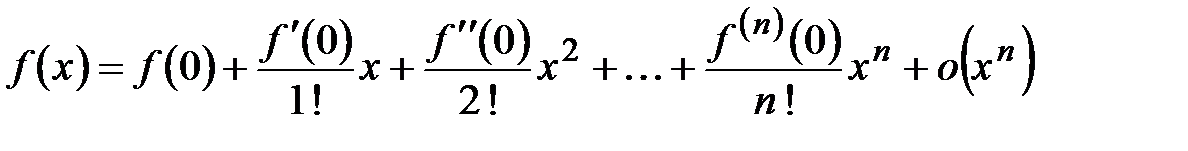 . (4.21) . (4.21)
Формулу (4.21) называют формулой Маклорена разложения функции  по степеням по степеням  с остаточным членом в форме Пеано. с остаточным членом в форме Пеано.
1. Пусть  . Вычислим производные функции . Вычислим производные функции  в точке в точке  : :  . .
Используя формулу (4.21), получим
 . .
В частности, при 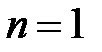 и и 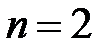 имеем: имеем:
 . .
2. Пусть 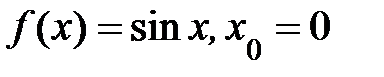 . Вычислим значения производных функции . Вычислим значения производных функции  при при  : :
 
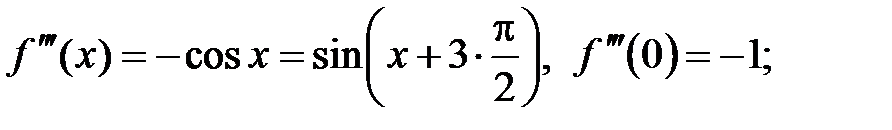
………………………………………………………………..
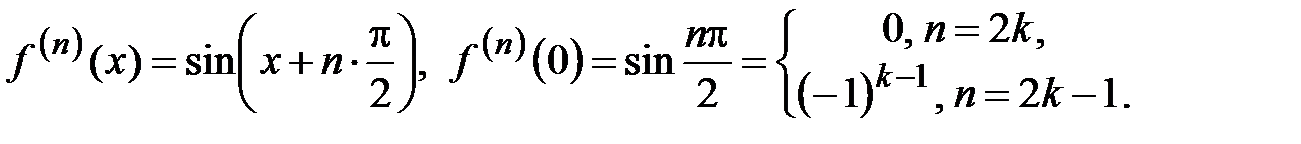
Используя формулу (4.21) при  , находим: , находим:
 . .
В частности, при  и и  имеем: имеем:
 . .
3. Разложение для  получается аналогично: получается аналогично:
 . .
В частности, при 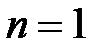 : :
 . .
4. Пусть  . Вычислим значения производных функции . Вычислим значения производных функции  при при  : :

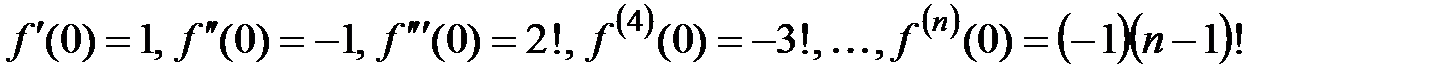
Тогда  . Используя формулу (4.21), получим: . Используя формулу (4.21), получим:
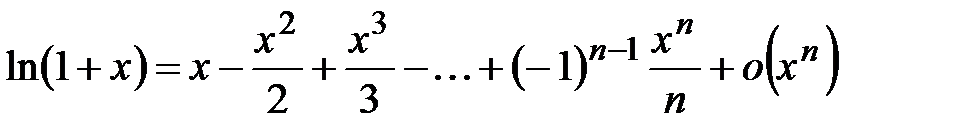 . .
В частности, при 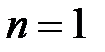
 . .
5. Аналогично получаем
 . .
Если  , то , то
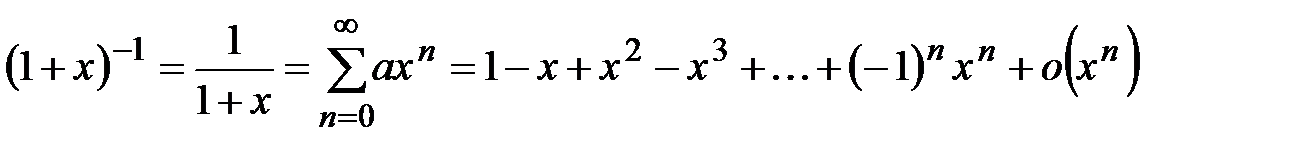 . .
Заменив 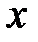 на на  , получим: , получим:
 . .
Пример 4.14.Разложить функцию 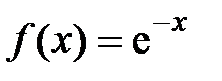 в ряд Маклорена с точностью в ряд Маклорена с точностью 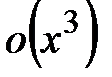 . .
Решение. Воспользуемся разложением  . Заменим . Заменим  на на  , получим , получим 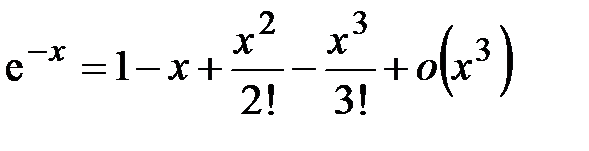 . .
| Рис. 4.6.Геометрическая иллюстрация примера 4.14
|
На рисунке 4.6 изображена кривая  , а также ее приближения , а также ее приближения  , ,  и и  . .
Пример 4.15.Разложить функцию  в окрестности точки в окрестности точки  , взяв , взяв  . .
Решение. Воспользуемся формулой Маклорена при  . Найдем производные . Найдем производные  , , 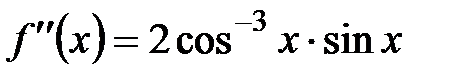 , ,  , отсюда , отсюда 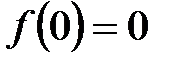 , ,  , ,  , ,  . Получаем . Получаем
 . .
Пример 4.16.Используя разложения функций по формуле Тейлора, вычислить пределы: а)  ; б) ; б)  . .
Решение. а) Воспользуемся разложениями:
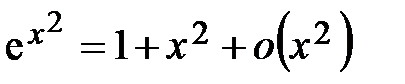 , ,  . Тогда . Тогда  . .
б) Если ограничиться разложением 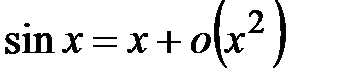 , то в пределе получаем выражение , то в пределе получаем выражение  . Чему равен такой предел, сказать невозможно. Неизвестно, какие бесконечно малые скрываются под . Чему равен такой предел, сказать невозможно. Неизвестно, какие бесконечно малые скрываются под  и и 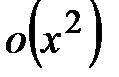 . Поэтому следует взять приближение . Поэтому следует взять приближение
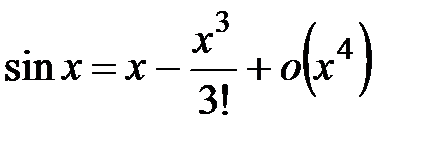 . Тогда . Тогда 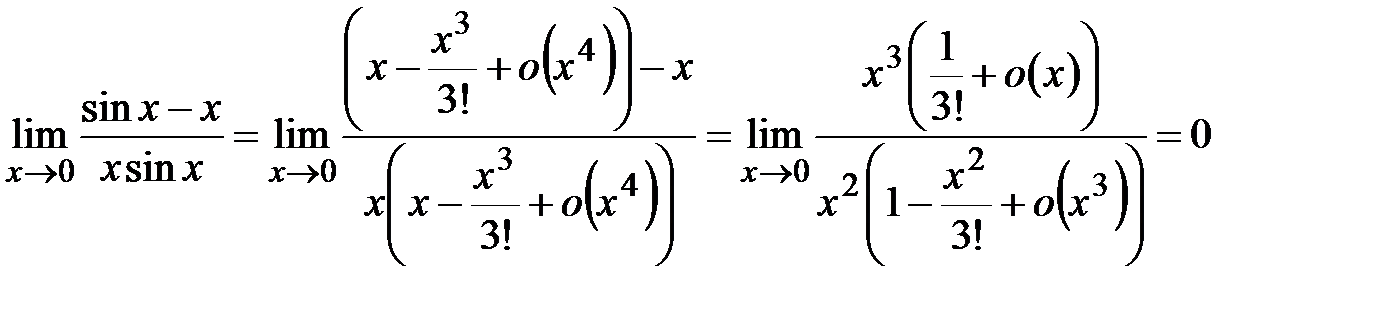 . .
Глава 5. Исследование и построение графиков функции одной переменной
Условия возрастания и убывания функции
Пусть функция  определена на интервале определена на интервале  . .
Определение. Функция  называется строго возрастающей (строго убывающей) на называется строго возрастающей (строго убывающей) на  , если для любых , если для любых  , верно неравенство , верно неравенство   . Функция . Функция  возрастает (убывает) на возрастает (убывает) на  , если для любых , если для любых  верно неравенство верно неравенство  . .
Теорема 5.1 (о необходимом и достаточном условии возрастания (убывания) функции)
Пусть функция  непрерывна на непрерывна на  и дифференцируема и дифференцируема 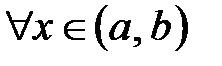 . Тогда: . Тогда:
1) для того чтобы функция 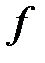 возрастала (убывала) на возрастала (убывала) на  , необходимо и достаточно, чтобы , необходимо и достаточно, чтобы 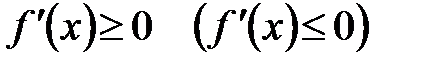 для всех для всех  ; ;
2) если производная 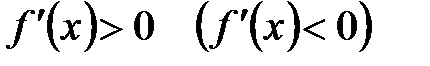 для всех для всех  , то функция , то функция 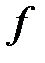 строго возрастает (строго убывает) на строго возрастает (строго убывает) на  . .
Доказательство.
1) Необходимость. Пусть  возрастает на возрастает на  . Покажем, что . Покажем, что 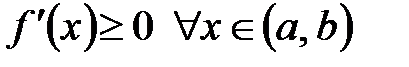 . Предположим противное, т. е. . Предположим противное, т. е. 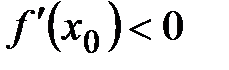 , ,  . Тогда по теореме Ферма (достаточные условия возрастания (убывания) функции в точке) функция . Тогда по теореме Ферма (достаточные условия возрастания (убывания) функции в точке) функция 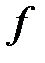 строго убывает в точке строго убывает в точке  , что противоречит тому, что , что противоречит тому, что  возрастает возрастает  . .
Достаточность. Пусть 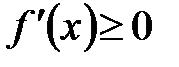 для всех для всех 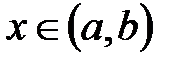 . Для любой пары точек . Для любой пары точек  таких, что таких, что  , функция , функция  на отрезке на отрезке  удовлетворяет условиям теоремы Лагранжа: удовлетворяет условиям теоремы Лагранжа:  , для которой , для которой  . Так как . Так как  , то , то  и, следовательно, и, следовательно,  . Т. о., мы доказали, что функция . Т. о., мы доказали, что функция  возрастает на возрастает на  . .
2) Пусть  для всех для всех 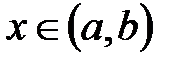 . По схеме доказательства предыдущего пункта с помощью формулы конечных приращений Лагранжа получаем . По схеме доказательства предыдущего пункта с помощью формулы конечных приращений Лагранжа получаем
 . .
Так как  , то , то  и если и если  , то , то 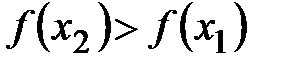 , то есть функция , то есть функция  возрастает в строгом смысле на возрастает в строгом смысле на  . .
Замечание. Условие 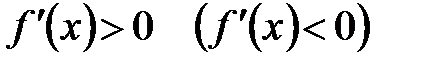 , будучи достаточным для строгого возрастания (убывания) функции, не является необходимым. Это видно на примере функции , будучи достаточным для строгого возрастания (убывания) функции, не является необходимым. Это видно на примере функции  , которая строго возрастает, но , которая строго возрастает, но  . .
Локальный экстремум
Теорема 5.2 (первое достаточное условие локального экстремума дифференцируемой функции)
| Рис. 5.1. Геометрическая иллюстрация теоремы 5.2
| Пусть функция 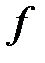 дифференцируема в некоторой окрестности дифференцируема в некоторой окрестности  критической точки критической точки  , за исключением, быть может, самой точки , за исключением, быть может, самой точки  , и непрерывна в точке , и непрерывна в точке  . Если при переходе через точку . Если при переходе через точку  слева направо производная слева направо производная  меняет знак с плюса на минус (с минуса на плюс), то в точке меняет знак с плюса на минус (с минуса на плюс), то в точке  функция функция 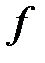 имеет строгий локальный максимум (минимум). имеет строгий локальный максимум (минимум).
Если же производная  имеет один и тот же знак слева и справа от точки имеет один и тот же знак слева и справа от точки  , то экстремума в этой точке нет. , то экстремума в этой точке нет.
Доказательство. Если производная  меняет знак с «+» на «–», то по теореме предыдущего пункта 5.1 (необходимое и достаточное условие возрастания (убывания) функции) функция меняет знак с «+» на «–», то по теореме предыдущего пункта 5.1 (необходимое и достаточное условие возрастания (убывания) функции) функция  возрастает для значений возрастает для значений  и и 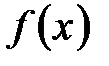 убывает для значений убывает для значений  . Следовательно, . Следовательно,  , то есть , то есть 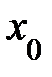 – точка локального максимума функции – точка локального максимума функции  (рис. 5.1). (рис. 5.1).
Аналогично доказывается теорема и в случае минимума.
Теорема 5.3. (второе достаточное условие локального экстремума дважды дифференцируемой функции)
Пусть функция 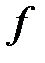 в критической точке в критической точке  имеет конечную вторую производную. Тогда функция имеет в точке имеет конечную вторую производную. Тогда функция имеет в точке  локальный максимум, если локальный максимум, если  , и локальный минимум, если , и локальный минимум, если  . .
Доказательство. Запишем формулу Тейлора для функции  в окрестности точки в окрестности точки  при при  : :
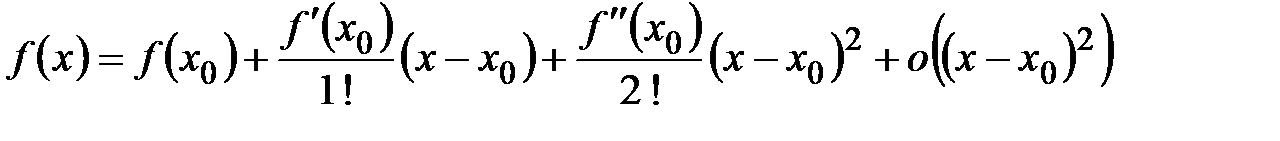 . .
По условию  , поэтому , поэтому  при при  . Если . Если   , то , то  , и, следовательно, , и, следовательно,  – точка локального минимума функции – точка локального минимума функции  . Если же . Если же   , то , то  , и, следовательно, , и, следовательно,  – точка локального максимума функции – точка локального максимума функции  . .
Пример 5.1. Доказать неравенство  для для  . .
Рассмотрим функцию  Имеем Имеем 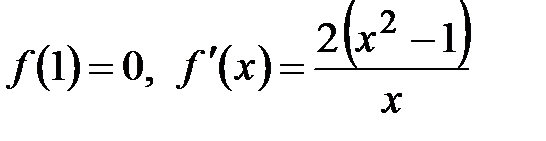 . Для . Для   а для а для   . Таким образом, . Таким образом,  на интервале на интервале 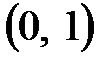 убывает, на интервале убывает, на интервале  возрастает, и так как возрастает, и так как  непрерывна при непрерывна при  , то точка , то точка  является точкой минимума. Следовательно, для является точкой минимума. Следовательно, для 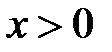   , откуда и вытекает неравенство , откуда и вытекает неравенство 
Пример 5.2. Исследовать на экстремум функцию 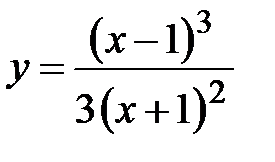 . .
Определим промежутки монотонности и экстремумы данной функции. Первая производная функции равна: 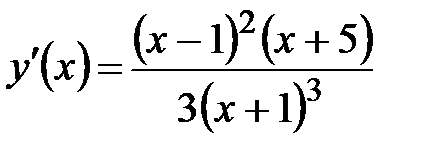 . Находим критические точки: . Находим критические точки:  при при  и и 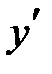 не существует при не существует при  . .
При  , при , при  . На каждом из промежутков . На каждом из промежутков  функция возрастает, на промежутке функция возрастает, на промежутке  убывает (рис. 5.2), в точке (-5; -4,5) имеет локальный максимум. Отметим, что убывает (рис. 5.2), в точке (-5; -4,5) имеет локальный максимум. Отметим, что  , т. е. график функции имеет в этой точке горизонтальную , т. е. график функции имеет в этой точке горизонтальную
 + - + + + - + +
| -1 
| х 
| | Рис. 5.2. Исследование знака производной и поведения функции из примера 5.2
|
касательную, точка  является критической, но локального экстремума у функции в этой точке нет, т. к. первая производная не меняет знак. Точка является критической, но локального экстремума у функции в этой точке нет, т. к. первая производная не меняет знак. Точка  также не является точкой экстремума (заданная функция в ней не определена), хотя производная при переходе через эту точку меняет знак. также не является точкой экстремума (заданная функция в ней не определена), хотя производная при переходе через эту точку меняет знак.
Пример 5.3. Исследовать на экстремум функцию  . .
Первая производная функции равна 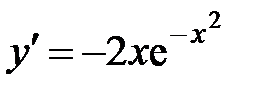 . Приравнивая производную нулю, находим единственную критическую точку . Приравнивая производную нулю, находим единственную критическую точку 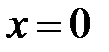 . Далее находим вторую производную . Далее находим вторую производную  . Ее значение в точке . Ее значение в точке 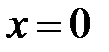 равно равно  . Согласно второму достаточному условию локального экстремума делаем вывод о наличии максимума функции и вычисляем . Согласно второму достаточному условию локального экстремума делаем вывод о наличии максимума функции и вычисляем  . .
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

 , а также ее приближения
, а также ее приближения  ,
,  и
и  .
.
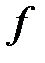 дифференцируема в некоторой окрестности
дифференцируема в некоторой окрестности  критической точки
критической точки  , за исключением, быть может, самой точки
, за исключением, быть может, самой точки  , и непрерывна в точке
, и непрерывна в точке  . Если при переходе через точку
. Если при переходе через точку  слева направо производная
слева направо производная  меняет знак с плюса на минус (с минуса на плюс), то в точке
меняет знак с плюса на минус (с минуса на плюс), то в точке  функция
функция 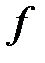 имеет строгий локальный максимум (минимум).
имеет строгий локальный максимум (минимум).
 является критической, но локального экстремума у функции в этой точке нет, т. к. первая производная не меняет знак. Точка
является критической, но локального экстремума у функции в этой точке нет, т. к. первая производная не меняет знак. Точка  также не является точкой экстремума (заданная функция в ней не определена), хотя производная при переходе через эту точку меняет знак.
также не является точкой экстремума (заданная функция в ней не определена), хотя производная при переходе через эту точку меняет знак.

 n раз непрерывно дифференцируема на
n раз непрерывно дифференцируема на  (т. е.
(т. е.  и эта функция непрерывна
и эта функция непрерывна  ) и имеет в каждой точке этого интервала, за исключением, быть может, точки
) и имеет в каждой точке этого интервала, за исключением, быть может, точки 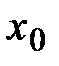 производную
производную  - го порядка. Тогда для любого
- го порядка. Тогда для любого  между
между 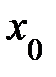 и х найдется такая точка
и х найдется такая точка  , что справедлива формула Тейлора
, что справедлива формула Тейлора ...
...  , (4.20)
, (4.20) – остаточный член в форме Лагранжа. Так как точка
– остаточный член в форме Лагранжа. Так как точка  , то
, то  , где
, где 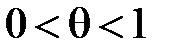 .
. :
: ...
... 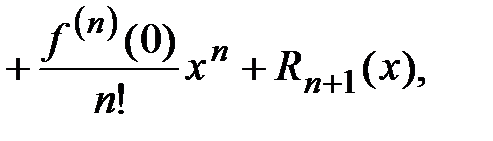
 ,
,  .
. по степеням
по степеням  .
. ,
, 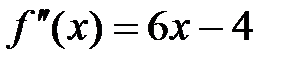 ,
,  ,
,  . Отсюда
. Отсюда
 .
. .
. . Таким образом,
. Таким образом, .
. по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки  .
. ,
, 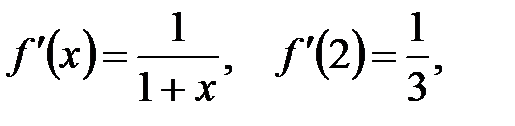

 … ,
… ,
 где 2 < x < x.
где 2 < x < x.

 ,
, 
 .
.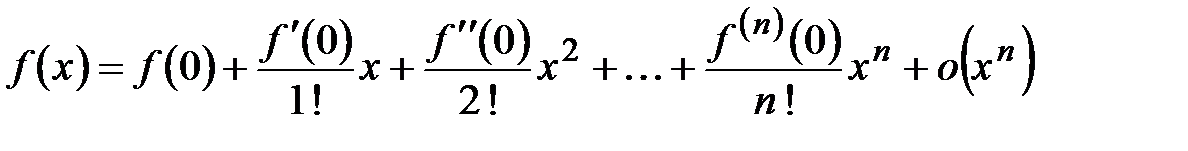 . (4.21)
. (4.21) по степеням
по степеням  с остаточным членом в форме Пеано.
с остаточным членом в форме Пеано. . Вычислим производные функции
. Вычислим производные функции  в точке
в точке  :
:  .
. .
.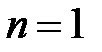 и
и 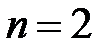 имеем:
имеем: .
.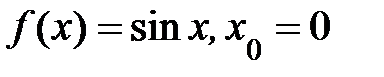 . Вычислим значения производных функции
. Вычислим значения производных функции  при
при  :
:

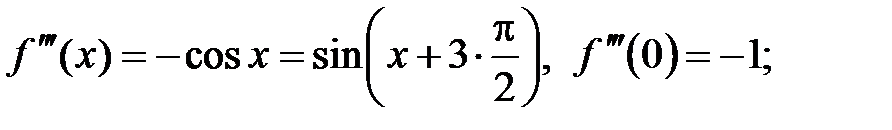
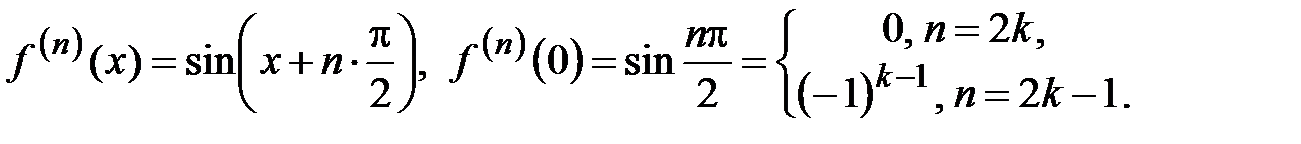
 , находим:
, находим: .
. и
и  имеем:
имеем: .
. получается аналогично:
получается аналогично: .
. :
: .
. . Вычислим значения производных функции
. Вычислим значения производных функции  при
при 
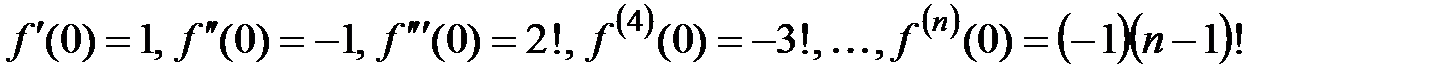
 . Используя формулу (4.21), получим:
. Используя формулу (4.21), получим: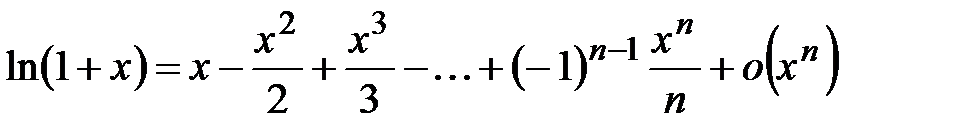 .
.
 .
. .
. , то
, то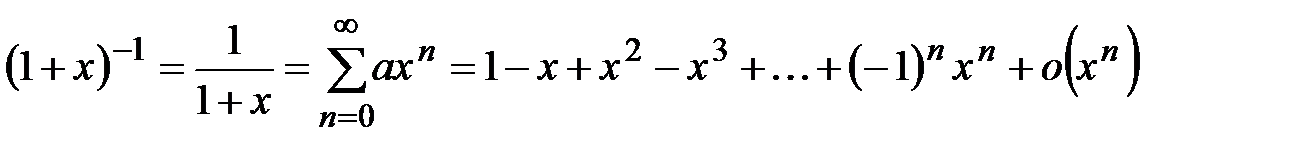 .
. на
на  , получим:
, получим: .
.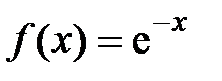 в ряд Маклорена с точностью
в ряд Маклорена с точностью 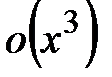 .
. . Заменим
. Заменим  на
на  , получим
, получим 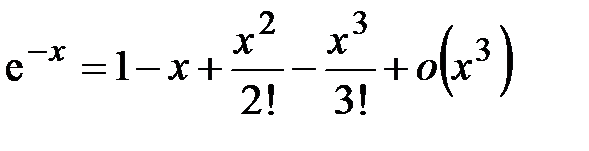 .
.





 в окрестности точки
в окрестности точки  , взяв
, взяв  .
. . Найдем производные
. Найдем производные  ,
, 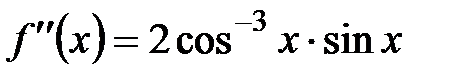 ,
,  , отсюда
, отсюда 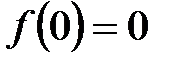 ,
,  ,
,  ,
,  . Получаем
. Получаем .
. ; б)
; б)  .
.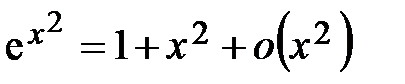 ,
,  . Тогда
. Тогда  .
.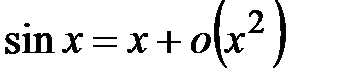 , то в пределе получаем выражение
, то в пределе получаем выражение  . Чему равен такой предел, сказать невозможно. Неизвестно, какие бесконечно малые скрываются под
. Чему равен такой предел, сказать невозможно. Неизвестно, какие бесконечно малые скрываются под  и
и 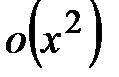 . Поэтому следует взять приближение
. Поэтому следует взять приближение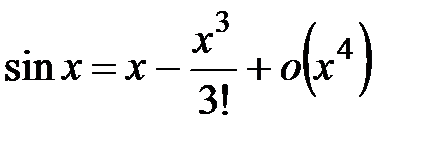 . Тогда
. Тогда 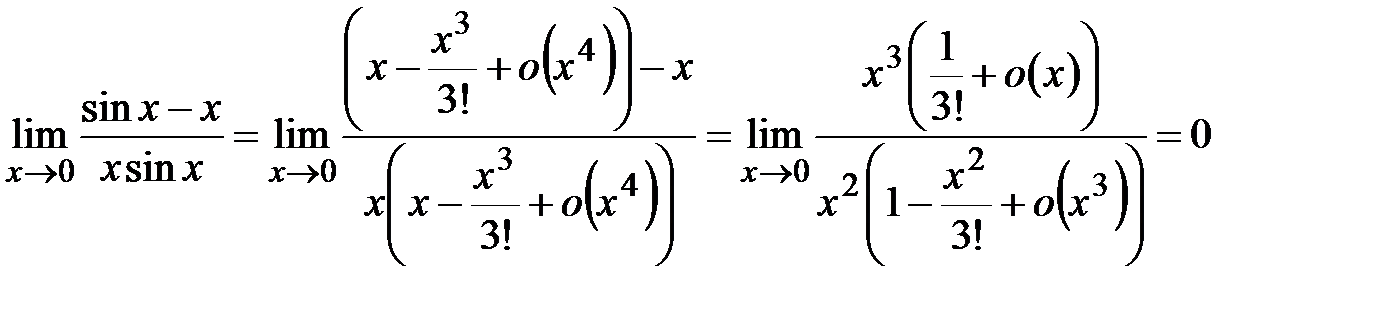 .
. определена на интервале
определена на интервале  .
. , верно неравенство
, верно неравенство 
 . Функция
. Функция  возрастает (убывает) на
возрастает (убывает) на  , если для любых
, если для любых  верно неравенство
верно неравенство  .
. и дифференцируема
и дифференцируема 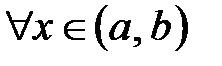 . Тогда:
. Тогда: , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы 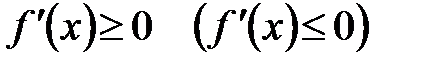 для всех
для всех  ;
;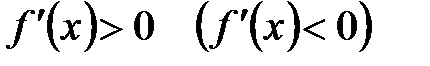 для всех
для всех  , то функция
, то функция 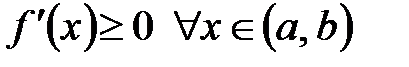 . Предположим противное, т. е.
. Предположим противное, т. е. 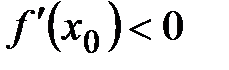 ,
,  . Тогда по теореме Ферма (достаточные условия возрастания (убывания) функции в точке) функция
. Тогда по теореме Ферма (достаточные условия возрастания (убывания) функции в точке) функция  , что противоречит тому, что
, что противоречит тому, что  возрастает
возрастает  .
.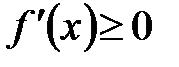 для всех
для всех 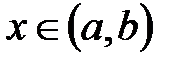 . Для любой пары точек
. Для любой пары точек  таких, что
таких, что  , функция
, функция  на отрезке
на отрезке  удовлетворяет условиям теоремы Лагранжа:
удовлетворяет условиям теоремы Лагранжа:  , для которой
, для которой  . Так как
. Так как  , то
, то  и, следовательно,
и, следовательно,  . Т. о., мы доказали, что функция
. Т. о., мы доказали, что функция  для всех
для всех  .
. , то
, то  и если
и если  , то
, то 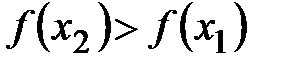 , то есть функция
, то есть функция  .
.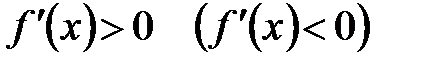 , будучи достаточным для строгого возрастания (убывания) функции, не является необходимым. Это видно на примере функции
, будучи достаточным для строгого возрастания (убывания) функции, не является необходимым. Это видно на примере функции  , которая строго возрастает, но
, которая строго возрастает, но  .
.

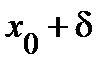


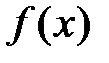
 и
и 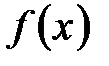 убывает для значений
убывает для значений  . Следовательно,
. Следовательно,  , то есть
, то есть 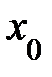 – точка локального максимума функции
– точка локального максимума функции  (рис. 5.1).
(рис. 5.1). имеет конечную вторую производную. Тогда функция имеет в точке
имеет конечную вторую производную. Тогда функция имеет в точке  , и локальный минимум, если
, и локальный минимум, если  .
. :
: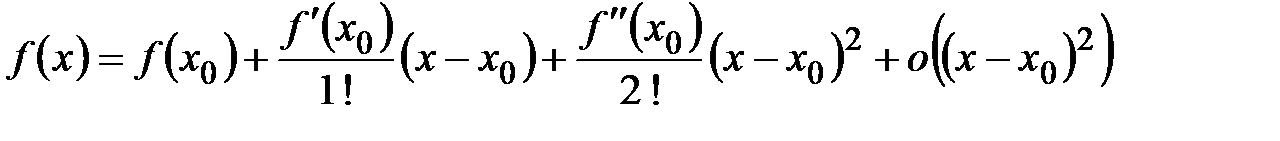 .
. , поэтому
, поэтому  при
при  . Если
. Если  , то
, то  , и, следовательно,
, и, следовательно,  – точка локального минимума функции
– точка локального минимума функции  . Если же
. Если же 
 , то
, то  , и, следовательно,
, и, следовательно,  для
для  .
. Имеем
Имеем 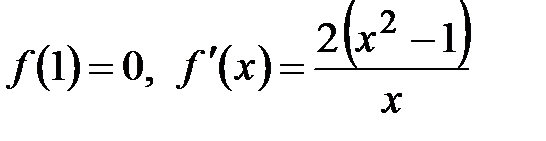 . Для
. Для 
 а для
а для 
 . Таким образом,
. Таким образом,  на интервале
на интервале  убывает, на интервале
убывает, на интервале  возрастает, и так как
возрастает, и так как  , то точка
, то точка 
 , откуда и вытекает неравенство
, откуда и вытекает неравенство 
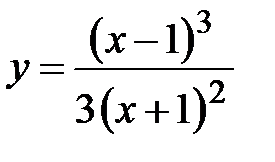 .
.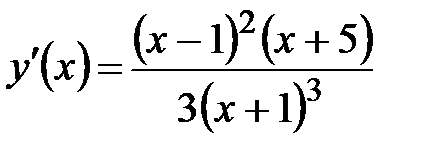 . Находим критические точки:
. Находим критические точки:  при
при  и
и 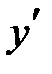 не существует при
не существует при  .
. , при
, при  . На каждом из промежутков
. На каждом из промежутков  функция возрастает, на промежутке
функция возрастает, на промежутке  убывает (рис. 5.2), в точке (-5; -4,5) имеет локальный максимум. Отметим, что
убывает (рис. 5.2), в точке (-5; -4,5) имеет локальный максимум. Отметим, что  , т. е. график функции имеет в этой точке горизонтальную
, т. е. график функции имеет в этой точке горизонтальную + - + +
+ - + +
 .
.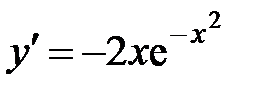 . Приравнивая производную нулю, находим единственную критическую точку
. Приравнивая производную нулю, находим единственную критическую точку 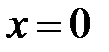 . Далее находим вторую производную
. Далее находим вторую производную  . Ее значение в точке
. Ее значение в точке  . Согласно второму достаточному условию локального экстремума делаем вывод о наличии максимума функции и вычисляем
. Согласно второму достаточному условию локального экстремума делаем вывод о наличии максимума функции и вычисляем  .
.