
|
|
Схема исследования функций и построения кривых1. Найти область определения функции 2. Отметить особенности функции (периодичность, четность и нечетность, сохранение знака), найти точки пересечения графика функции с осями координат. 3. Если граничные точки области определения функции принадлежат ей, то найти значение функции в этих точках, в противном случае – выяснить поведение функции в окрестности этих точек. Найти вертикальные асимптоты, если они существуют. 4. Исследовать поведение функции при 5. Найти интервалы монотонности функции и точки экстремума. 6. Указать интервалы сохранения направления выпуклости и точки перегиба графика функции. По результатам исследования функции строится ее график. Пример 5.11.Исследовать функции и построить их графики:
1. А) Область определения функции Б) Вертикальных асимптот нет, т. к. функция непрерывна при всех
В)
 . Находим критические точки: . Находим критические точки:  при при  и и  не существует при не существует при  . При . При  и при и при   , при , при  . На каждом из промежутков . На каждом из промежутков  функция убывает, на промежутке функция убывает, на промежутке  функция возрастает (рис. 5.12) . функция возрастает (рис. 5.12) .
Точка локального минимума Г) Определим промежутки выпуклости и точки перегиба графика функции. Вторая производная равна
Точки перегиба графика функции  . Здесь . Здесь   . График функции представлен на рис. 5.14. . График функции представлен на рис. 5.14.
2. Область определения А) Вертикальных асимптот нет, так как функция определена и непрерывна на множестве действительных чисел. Для наклонной асимптоты
т. е. Б) Найдем производную
При 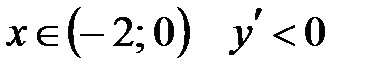 ; при ; при  . На промежутке . На промежутке  функция убывает, на промежутках функция убывает, на промежутках  возрастает (рис. 5.15). В точке (-2; возрастает (рис. 5.15). В точке (-2;  ) функция имеет локальный максимум, в точке ) функция имеет локальный максимум, в точке  локальный минимум. Отметим, что локальный минимум. Отметим, что  , т. е. график функции имеет в этой точке горизонтальную касательную. В точке (-3; 0) имеем вертикальную касательную , т. е. график функции имеет в этой точке горизонтальную касательную. В точке (-3; 0) имеем вертикальную касательную  (функция (функция  в точке в точке  непрерывна и непрерывна и  ). Поскольку ). Поскольку  непрерывна в нуле и непрерывна в нуле и  ; то полупрямая ; то полупрямая  , ,  является и левой и правой полукасательной к графику функции в точке является и левой и правой полукасательной к графику функции в точке 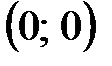 . .
Определим промежутки выпуклости и точки перегиба графика функции. Находим вторую производную
График функции представлен на рис. 5.17.
[1] Жозеф Луи Лагранж (1736–1813) – знаменитый французский математик и механик, член Парижской АН. Ему принадлежат выдающиеся исследования по различным вопросам математического анализа, теории чисел, алгебре, дифференциальным уравнениям, астрологии и др.
[2] Исаак Ньютон (1642–1727) – английский физик, механик, астроном и математик. Разработал (наряду с Лейбницем) основы дифференциального и интегрального исчисления.
[3] Готфрид Вильгельм Лейбниц (1646–1716) – немецкий философ-идеалист, физик, математик, изобретатель, историк. В математике важнейшей заслугой Лейбница (наряду с И.Ньютоном и независимо от него) является разработка дифференциального и интегрального исчисления. Лейбниц изобрел первый интегрирующий механизм и уникальную для того времени счетную машину.
[4] Пьер Ферма (1601–1665 гг.) – выдающийся французский математик, по профессии юрист. Ферма является одним из создателей теории чисел. Сформулированная им теорема о том, что уравнение [5] Мишель Ролль (1652 –1719 гг.) – французский математик. Его исследования были не замечены и забыты современниками, и по достоинству оценены намного позже. [6] Коши Огюстен Луи (1789–1857) – французский математик, один из наиболее активных творцов современного языка и аппарата классического анализа.
[7] Иоганн Бернулли (1667–1748) – швейцарский математик, младший брат Якоба Бернулли. Сотрудничал с Лейбницем в разработке дифференциального и интегрального исчислений. Продвинул теорию дифференциальных уравнений, исследования в области механики и др. [8] Лопиталь Гийом Франсуа Антуан (1661–1704) – французский математик, автор первого учебника по дифференциальному исчислению (1696), в основу которого легли лекции швейцарского математика Иоганна Бернулли. [9] Брук Тейлор (1685 –1731) – английский математик. Ему принадлежат заслуги в разработке теории конечных разностей, автор работ о полете снарядов, взаимодействии магнитов, капиллярности и др. [10] Джузеппе Пеано (1858 – 1932) – итальянский математик. Занимался формально логическим обоснованием математики. Известен его пример непрерывной (жордановой) кривой, целиком заполняющей некоторый квадрат. [11] Колин Маклорен (1698–1746) – шотландский математик. Математические исследования относятся к анализу (теория рядов, конечные разности), ряд работ к механике. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. и при
и при  , найти горизонтальные или наклонные асимптоты или убедиться в их отсутствии.
, найти горизонтальные или наклонные асимптоты или убедиться в их отсутствии. ;
;
 .
.
 .
.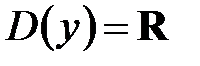 ;
;  при
при  ,
,  .
. . Найдем наклонные асимптоты
. Найдем наклонные асимптоты  :
: ;
; ;
; .
. имеем правую горизонтальную асимптоту
имеем правую горизонтальную асимптоту ; при
; при  наклонных и горизонтальных асимптот нет.
наклонных и горизонтальных асимптот нет. - + -
- + -

 ; локального максимума
; локального максимума  ; в точке
; в точке  – вертикальная полукасательная
– вертикальная полукасательная 
 .
. . Найдем корни уравнения
. Найдем корни уравнения  :
: 
 . Так как
. Так как  при
при 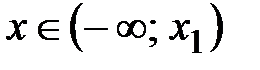 и при
и при  , то на этих интервалах график функции является выпуклым вниз. Аналогично при
, то на этих интервалах график функции является выпуклым вниз. Аналогично при  , т. е. на соответствующих интервалах график функции выпуклый вверх, рис. 5. 13.
, т. е. на соответствующих интервалах график функции выпуклый вверх, рис. 5. 13.









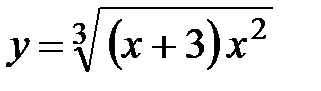 .
. при
при  и при
и при  . При
. При  , а при
, а при  . Точки
. Точки  и
и  являются точками пересечения графика функции с осями координат.
являются точками пересечения графика функции с осями координат. найдем коэффициенты:
найдем коэффициенты:

 – наклонная асимптота.
– наклонная асимптота. ;
;  при
при  и
и  не существует при
не существует при  и при
и при  .
.

 + + - +
у х
+ + - +
у х
 . Знаки второй производной:
. Знаки второй производной:  при
при  и при
и при  ,
,  при
при  (рис. 5.16). Точка перегиба графика функции
(рис. 5.16). Точка перегиба графика функции  . На промежутке
. На промежутке  график функции выпуклый вниз; на промежутках
график функции выпуклый вниз; на промежутках 



 не разрешимо в целых числах, была доказана только в 1994 г. Эндрю Уайлсом.
не разрешимо в целых числах, была доказана только в 1994 г. Эндрю Уайлсом.