
|
|
Закономерности распределения молекул по координатам в состоянии термодинамического равновесия
Вспомним ещё раз все известные нам признаки состояния термодинамического равновесия: а) температура не зависит от времени и от координат точки системы, то есть в системе нет потоков энергии; б) давление в системе не зависит от времени, но как мы увидим может меняться от точки к точке, если газ находится во внешнем силовом поле; в) постоянны масса и число частиц каждого компонента смеси; г) молекулы газа движутся хаотически, не существует преимущественного направления движения, т.е. в системе нет потоков частиц. Проанализируем вопрос о распределении молекул по координатам (по объему). Если бы подобная задача ставилась для динамической системы нужно было бы задать для каждого элемента системы его радиус-вектор. Мы уже знаем, что для системы большого числа частиц подобное описание невозможно и необходимо использовать вероятностное описание. В рамках этого описания можно определить только вид распределения по координатам только средних значений величин, например средней концентрации частиц, температуры (характеризующей среднее значение кинетической энергии молекул). Но концентрацию или температуру в выбранной точке пространства определить невозможно. Для проведения этой операции нужно выделить конечный объем. Число частиц в выделенном объеме флуктуирует (изменяется с течением времени), поэтому его выбирают таким, чтобы количество частиц в этом объеме было достаточным для усреднения. Выполнение последнего требования обеспечивается, если выбранный объем DV много больше объема, приходящегося на одну молекулу Vм., т.е. объем V, занимаемый системой, нужно разбить на множество объемов, которые, для нахождения распределения должны быть много меньше объема системы. Итак, чтобы найти вид распределения в атомно-молекулярной системе, необходимо сначала произвести разбиение занимаемого системой объема на элементы DV так, чтобы выполнялось двойное неравенство
Оценим на конкретных примерах величину объема DV. Предположим, необходимо составить карту распределения температуры в аудитории, тогда условию (43) удовлетворяет объем DV=1 см3. Когда нужно определить распределение давления в атмосфере, высота которой порядка 300 км, в качестве физически бесконечно малого объема можно принять 1 км3. Итак, будем искать распределения в среднем, т.е. производить усреднения величин, для которых устанавливается вид распределения, в физически бесконечно малом объеме. Рассмотрим объем газа V, находящийся в состоянии термодинамического равновесия в отсутствие внешних полей. Все области такой системы трансляционно симметричны. Это значит, что температура и концентрация частиц не зависят от времени и координат. Подобная ситуация реализуется только для изолированных систем. Рассмотрим газ, находящийся в силовом поле. Пусть напряженность поля направлена горизонтально. Выберем ось ОХ совпадающей с направлением напряженности поля. Выделим физически бесконечно малый объем dV - параллелепипед с основанием, перпендикулярным линии действия силы и высотой dx (рис. 1.6.1).
РИСУНОК Рис. 1.6.1. К выводу распределения Больцмана
Определим силу, действующую на выделенный элемент в рассматриваемом потенциальном поле. С одной стороны, в поле этой силы каждая молекула имеет потенциальную энергию
откуда, учитывая, что
С другой стороны, сила, действующая на бесконечно малый объем может быть определена произведением приращения давления, создаваемого на dx и пощади
Учтем, что рассматривается модель идеального газа, для которого при постоянной температуре
Решением уравнение (47) с граничным условием: при
Данной функцией задается вид распределения Больцмана молекул по координатам. Чтобы в этом убедиться, запишем явно вид функции распределения молекул по координатам
Подстановка в последнее выражение распределения Больцмана дает
Конкретный вид функции распределения задается, если известно силовое поле, в котором находится система. Распределение Больцмана здесь получено для идеального газа, однако оно справедливо для любых систем классических частиц, чем и воспользовался Перрен для экспериментальной проверки справедливости распределения Больцмана в форме (48). Так как при получении распределения Больцмана в силовом поле на массу и размер частиц ограничений не накладывалось, значит можно предположить, что оно справедливо и для макрочастиц любой массы, взаимодействие между которыми можно пренебречь. Массы макрочастиц могут быть экспериментально измерены, и их число подсчитано. Однако в обычных условиях все макрочастицы будут находиться вблизи дна сосуда и получить экспериментально вид распределения не удастся. Выход в 1906 году нашел французский физик Жак Перрен. Он предложил и провел опыты по проверке распределения Больцмана, поместив в жидкость макроскопические частицы гуммигута, представлявшие собой шарики одинакового радиуса. То есть частицы находятся в потенциальном поле силы тяжести с потенциальной энергией mgh и поле Архимедовой силы. Выталкивающая сила в пределах жидкости является потенциальной и потенциальная энергия в этом поле находится как
а распределение Больцмана для рассматриваемого случая
откуда после логарифмирования обеих частей с учетом соотношения между постоянными Больцмана, Авогадро и универсальной газовой постоянной
Подсчет числа частиц проводился с помощью микроскопа. Полученные результаты подтвердили экспоненциальное уменьшение концентрации частиц с высотой. Справедливость для системы макрочастиц распределения Больцмана позволила Перрену экспериментально определить число Авогадро. Из опытов следовало, что NA=6,5*1023 ¸ 7,5*1023 моль-1.
Считая газ идеальным, можно найти вид зависимости давления от высоты h
где Изобразим вид функции распределения по высоте молекул равновесной атмосферы, состоящей из молекул одного сорта (рис.___).

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . (43)
. (43) и на нее действует сила
и на нее действует сила  . Искомая же сила может быть найдена как сумма сил, действующих в этом потенциальном поле на молекулы
. Искомая же сила может быть найдена как сумма сил, действующих в этом потенциальном поле на молекулы 
 , (44)
, (44)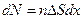 , получаем
, получаем . (45)
. (45) , на которую эта сила действует:
, на которую эта сила действует: . (46)
. (46) и приравняем соотношения (45) и (46). В результате получим дифференциальное уравнение:
и приравняем соотношения (45) и (46). В результате получим дифференциальное уравнение: . (47)
. (47)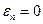
 является функция
является функция . (48)
. (48) , определяющую долю молекул, имеющих одновременно координаты в интервалах
, определяющую долю молекул, имеющих одновременно координаты в интервалах  ,
,  ,
, 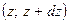
 . (49)
. (49) . (50)
. (50) . В таком случае полная потенциальная энергия одной частицы гуммигута объема V и плотности rг может быть записана в виде
. В таком случае полная потенциальная энергия одной частицы гуммигута объема V и плотности rг может быть записана в виде , (51)
, (51) , (52)
, (52) получаем выражение для вычисления постоянной Авогадро:
получаем выражение для вычисления постоянной Авогадро: (53)
(53) Рассмотрим теперь столб газа, находящийся в поле силы тяжести, тогда
Рассмотрим теперь столб газа, находящийся в поле силы тяжести, тогда . (54)
. (54) , (55)
, (55) - давление на высоте
- давление на высоте  . Функция (55) называется барометрической формулой. Она справедлива, если температура остается постоянной, это условие использовано при получении уравнения (47). Таким образом, барометрическая формула справедлива для изотермической (равновесной) атмосферы.
. Функция (55) называется барометрической формулой. Она справедлива, если температура остается постоянной, это условие использовано при получении уравнения (47). Таким образом, барометрическая формула справедлива для изотермической (равновесной) атмосферы.