
|
|
Закономерности распределения молекул по абсолютным значениям скорости в состоянии термодинамического равновесияРаспределение молекул по проекциям скорости в состоянии термодинамического равновесия Функция распределения На систему, состоящую из большого числа частиц, могут действовать силы, учет которых принципиально невозможен. Такие воздействия носят случайный характер и называются стохастическими. Они могут быть связаны с молекулярным (микроскопическим) движением, оказывающим влияние на поведение макроскопической системы. Широко распространены явления, когда стохастические воздействия оказывают определяющее влияние на поведение системы, т.е. выполняется неравенство Для определения характера поведения системы, на которую оказывается стохастическое воздействие, необходимо установить вид функции распределения. Функция распределения характеризует особенности стохастических воздействий в анализируемом процессе. Макроскопическую систему, т.е. совокупность большого числа микрочастиц, представляющую собой идеальный газ, как раз и характеризует определяющее влияние стохастических сил, а параметры ее определяются функциями распределения. Каждая микрочастица, входящая в состав макросистемы, обладает некоторой скоростью, энергией, имеет определенные координаты. У различных микрочастиц все эти величины могут быть различными, хотя могут частично совпадать. Пусть общее число частиц макросистемы N. Обозначим через dN(u)-число частиц, имеющих скорости в интервале от u до u+du (du-элементарное приращение). Ясно, что чем больше общее число частиц N и чем больше интервал скоростей du,тем больше будет dN: dN(u)~N, dN(u)~du. Коэффициент пропорциональности для различных значений u может быть разным, поэтому можно записать dN(u)=f(u)Ndu, (1) Функция f(u) и есть функция распределения микрочастиц по скоростям (аналогично, по координатам, энергии). Ясно, что dN/N показывает, какая часть частиц имеет скорости в интервале от u до u+du , т.е. вероятность того, что частицы имеют скорость в этом интервале. Если dN/N, т.е. вероятность, разделить на du , т.е. на интервал возможных значений параметра, то мы получим плотность вероятности. Таким образом, функция распределения - суть плотность вероятности обнаружения микрочастицы с заданным значением параметра (скорость, координата, энергия). Поскольку òdN=N, то получим
т.е. Для описания макросистемы применяют различные виды функции распределения: - функция распределения по компонентам скорости; - функция распределения по абсолютному значению скоростей; - функция распределения по координатам; - функция распределения по скоростям и координатам; - функция распределения по энергии.
dN(x, y, z)=f( x, y, z) N dxdydz – число частиц, попадающих в элементарный объем dxdydz=dV- (рис. а).
В общем случае определяют вероятность обнаружения микрочастицы в единичных интервалах вблизи некоторого значения координат и компонент скорости dN(ux, uy, uz,x, y ,z)=f(ux, uy, uz ,x, y, z)N duxduyduz dxdydz, (5) Что же даёт нам знание функции распределения некоторой системы? Во-первых, функция распределения показывает, в каком интервале могут находиться параметры (скорости, координаты, энергия) микрочастиц системы и какие значения параметров наиболее вероятны. Во- вторых, функция распределения позволяет определять средние значения физических величин макросистемы, зависящих от координат и скоростей. А именно, средние значения проявляются и определяются на опыте. Термодинамическое равновесие – наиболее простое состояние молекулярной системы – системы многих частиц. В этом состоянии господствует хаос молекулярного движения, нет преимущественных потоков частиц, энергии, вообще нет никаких макроскопических потоков. Однако же молекулярное движение существует. Как мы уже знаем, его средняя кинетическая энергия в расчете на одну молекулу идеального газа, материальную точку массой m, равна (3/2)kT. Получить закономерность распределения молекул по скоростям – сложная задача даже в условиях термодинамического равновесия. Однако простота состояния хаоса позволила Максвеллу если не вывести, то во всяком случае, как это понятно с позиций современности, догадаться, какой вид должна иметь эта зависимость. Следуя Максвеллу, отметим, что состояние хаоса позволяет нам сделать вывод о полной независимости движения моделирующих молекулы материальных точек по всем трем степеням свободы. Это значит, что функции распределения молекул по компонентам скоростей vx vy vz должны иметь одинаковый вид f(vx) = f(vy) = f(vz). С другой стороны, если события, в которых молекула имеет значения компонентов скоростей vx vy vz независимы, то вероятность одновременно иметь значения компонентов vx vy vz определяется произведением соответствующих вероятностей:
f(vx vy vz) = f(vx)×f(vy)×f(vz). (6)
Что же можно сказать о виде функции f(vi) ? Из тех же закономерностей хаоса очевидно, что функция распределения по компонентам скоростей является симметричной относительно изменения знака компоненты скорости, f(vi) = -f(vi). Это означает, что f(vi) является четной функцией компонентов скорости, в простейшем случае – четной степени компонентов скорости. Но какой степени? Здесь нам поможет обращение к механике. При анализе механического движения мы встречались с функцией скорости, прежде всего – импульсом, и функцией квадрата скорости – кинетической энергией. Из физических соображений ясно, что, как это полагал Максвелл, искомой четной функцией от скорости является кинетическая энергия:
В результате, соотношение (1) может быть представлено в виде:
Прологарифмируем соотношение (3), чтобы перейти от произведения к сумме функций:
Так как
при то при E(v) = const, f(v) = const, в том числе, при изменении соотношения между вкладами в кинетическую энергию при движении по отдельным степеням свободы. При учете этого условия продифференцируем соотношение (4) по вкладам в кинетическую энергию, соответствующим движению по отдельным степеням свободы.
Вследствие симметрии функции f(v) левые части уравнений (11-13) равны. Тогда следует, что правые части этих уравнений должны быть равны некоторой универсальной величине, не зависящей от скорости или какой либо ее компоненты (проекции).
В этом случае, для любой из компонент (проекций)
Интегрирование дает:
Постоянную Ai можно определить из условия нормировки:
Откуда
Знание функции распределения молекул по компонентам (проекциям) скорости обеспечивает возможность определения средней величины кинетической энергии, обусловленной движением по данной степени свободы:
На основе кинетической теории уже было получено, что средняя энергия, приходящаяся на одну степень свободы, равна (1/2)kT, откуда следует, что a = (1/kT). Итак, функция распределения молекул по проекциям скоростей на ось ОХ имеет вид:
Аналогичный вид имеют функции распределения молекул по проекциям скоростей на оси ОY и OZ:
Теперь легко определить вероятность
где функцию Учитывая вид функций распределения молекул по модулям скоростей (20), (21), (22), получаем
Графики функций (20) – (22) и (24) симметричны относительно начала координат
Рис. График функции распределения молекул по проекциям скорости на ось ОХ
Рис. 1.5.??. График функции распределения молекул по векторам скоростей в ??двумерном случае. Закономерности распределения молекул по абсолютным значениям скорости в состоянии термодинамического равновесия
Однако, можно поступить проще, воспользовавшись сферической симметрией распределения молекул по абсолютным значениям скорости в состоянии термодинамического равновесия. Определим выражение для объема дифференциально тонкого сферического слоя в пространстве скоростей
Тогда вероятность того, что молекула будет иметь значение скорости в интервале
Итак, функция распределения молекул по абсолютным значениям скорости имеет вид
Функция (28) носит название распределения Максвелла по скоростям. Площадь под графиком функции (рис.1.6.1) равна единице (функция нормирована на единицу). Физически это означает, что вероятность молекуле иметь скорость в интервале
При получении выражений для функций распределения молекул по проекциям, векторам и абсолютным значениям скорости явно использовалось, что газ находится в состоянии термодинамического равновесия, которое является наиболее вероятным для изолированной системы. В этом состоянии движение молекул максимально хаотично и для него справедливо распределение Максвелла. Выше мы видели, что температура определяется средней кинетической энергией молекул, теперь понятно, что она определяется средней кинетической энергией хаотического движения. Скорость направленного движения газа может быть различной, а температура одной и той же. Таким образом, температура измеряется в системе отсчета, в которой газ, как целое, покоится. Распределения были получены для закономерностей распределения по скоростям молекул идеального газа, однако распределения справедливы для систем многих невзаимодействующих частиц, в поведении которых не проявляются квантовые эффекты, если система находится в состоянии термодинамического равновесия. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
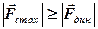 . Когда для системы выполняется это условие, связь между состояниями не является взаимно однозначной, а поведение системы подчиняется вероятностным закономерностям, на основе которых по известному набору параметров состояния в некоторый момент времени определяется вероятность состояния.
. Когда для системы выполняется это условие, связь между состояниями не является взаимно однозначной, а поведение системы подчиняется вероятностным закономерностям, на основе которых по известному набору параметров состояния в некоторый момент времени определяется вероятность состояния.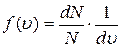 (2)
(2)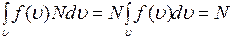 , (3)
, (3)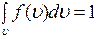 - это условие нормировки функции распределения, которое означает, что вероятность обнаружить частицу с данным значением скорости во всем диапазоне скоростей от -¥ до + ¥ равна 1.
- это условие нормировки функции распределения, которое означает, что вероятность обнаружить частицу с данным значением скорости во всем диапазоне скоростей от -¥ до + ¥ равна 1.

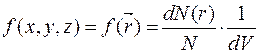 (4)
(4) . (7)
. (7)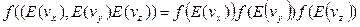 (8)
(8)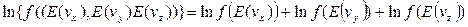 (9)
(9) (10)
(10)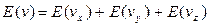 ,
,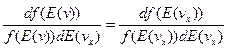 (11)
(11)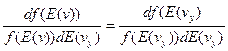 (12)
(12) (13)
(13)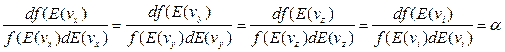 (14)
(14)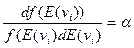 ,
, 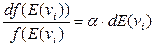 (15)
(15)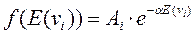 (16)
(16)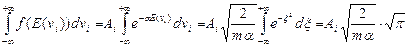 (17)
(17)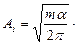 (18)
(18)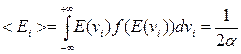 . (19)
. (19)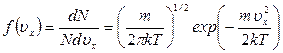 . (20)
. (20)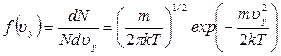 , (21)
, (21) . (22)
. (22)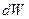 того, что молекула одновременно имеет проекции скорости в интервалах
того, что молекула одновременно имеет проекции скорости в интервалах  ,
, 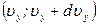 ,
, 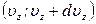 . Или, согласно эргодической гипотезе, долю молекул, имеющих одновременно проекции скорости в указанных интервалах
. Или, согласно эргодической гипотезе, долю молекул, имеющих одновременно проекции скорости в указанных интервалах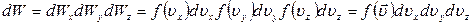 , (23)
, (23) можно трактовать как функцию распределения молекул по векторам скоростей. В пространстве скоростей вероятность, задаваемая последним выражением, показывает вероятность того, что конец вектора скорости молекулы попадает в параллелепипед с ребрами
можно трактовать как функцию распределения молекул по векторам скоростей. В пространстве скоростей вероятность, задаваемая последним выражением, показывает вероятность того, что конец вектора скорости молекулы попадает в параллелепипед с ребрами 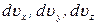 вблизи точки с координатами
вблизи точки с координатами 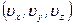 .
.
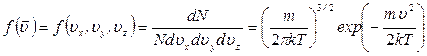 . (24)
. (24)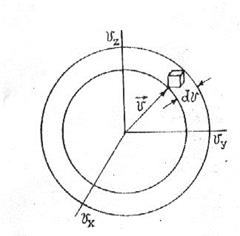 Найдем теперь вид функции распределения молекул по абсолютным значениям скорости. То есть теперь нас не будет интересовать направление скорости молекул, следовательно, необходимо определить вероятность того, что конец вектора скорости в пространстве скоростей попадет в сферический слой толщиной dv вблизи сферы радиуса v (рис.).
Найдем теперь вид функции распределения молекул по абсолютным значениям скорости. То есть теперь нас не будет интересовать направление скорости молекул, следовательно, необходимо определить вероятность того, что конец вектора скорости в пространстве скоростей попадет в сферический слой толщиной dv вблизи сферы радиуса v (рис.).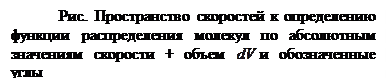
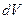 (рис.) по всем возможным значениям углов
(рис.) по всем возможным значениям углов . (25)
. (25)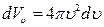 . (26)
. (26)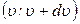
 . (27)
. (27)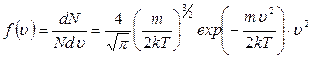 . (28)
. (28) равна единице или, что доля молекул, имеющих скорость в указанном интервале равна единице.
равна единице или, что доля молекул, имеющих скорость в указанном интервале равна единице.
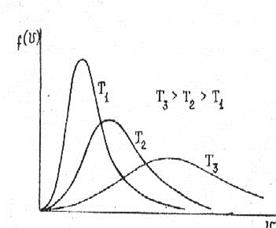 В отличие от функций распределения молекул по проекциям скорости, функция распределения по модулям скорости несимметрична относительно максимума. Это различие становится понятным из следующих рассуждений. Функция распределения молекул по векторам скоростей характеризует число частиц, приходящихся на единичный объем
В отличие от функций распределения молекул по проекциям скорости, функция распределения по модулям скорости несимметрична относительно максимума. Это различие становится понятным из следующих рассуждений. Функция распределения молекул по векторам скоростей характеризует число частиц, приходящихся на единичный объем  в пространстве скоростей. Величина этого объема не зависит от его положения в пространстве скоростей, и распределение равномерно. В случае функции распределения молекул по абсолютным значениям скоростей (28) единичный объем есть объем сферического слоя
в пространстве скоростей. Величина этого объема не зависит от его положения в пространстве скоростей, и распределение равномерно. В случае функции распределения молекул по абсолютным значениям скоростей (28) единичный объем есть объем сферического слоя 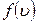 вносят два типа зависимости: экспоненциальная от квадрата скорости, определяющая вид функции (28), и изменение объема слоя (рис.??) в пространстве скоростей. При скоростях, близких к нулю, большее значение имеет первая тенденция, при больших значениях скоростей вид функции
вносят два типа зависимости: экспоненциальная от квадрата скорости, определяющая вид функции (28), и изменение объема слоя (рис.??) в пространстве скоростей. При скоростях, близких к нулю, большее значение имеет первая тенденция, при больших значениях скоростей вид функции