
|
|
Характерные скорости распределения Максвелла
Найдем координаты максимума функции распределения молекул по абсолютным значениям скорости. Для этого вычислим производную функции (28) и приравняем ее к нулю. Значение коэффициента, стоящего перед экспонентой не повлияет на результат, то есть
Вычислив производную (29), получим
откуда находим скорость, на которую приходится максимум функции распределения молекул по скоростям, называемую наивероятнейшей скоростью:
Максимум функции распределения молекул по векторам скоростей (24) приходится на значения проекций скорости, равные нулю. Заметим, что в показателе экспоненты в функции распределения (28) стоит выражение, определяющее квадрат наивероятной скорости, и запишем функцию распределения молекул по модулям скорости в виде:
а вероятность для частицы иметь скорость в интервале
Выполним в (33) замену переменной. Введем новую переменную
Следовательно, функция распределения молекул по значениям относительной скорости Максвеллаимеет вид
В функцию распределения по относительным скоростям не входит ни одной характеристики отдельной молекулы, максимум этой функции приходится, очевидно на u=1. Таким образом, функция распределения (35) справедлива для любого идеального газа, находящегося в термодинамическом равновесии, то есть является универсальной зависимостью. Функция распределения ‑ конечный результат описания вероятностной закономерности. Полученные выше функции распределения характеризуют систему в состоянии термодинамического равновесия, поэтому не зависят от времени, ни явно, ни неявно. Используя функции распределения, можно вычислять средние значения параметров состояния системы, которые, естественно могут быть определены и экспериментально. Как тестовую задачу для метода, основанного на использовании функции распределения, рассмотрим вычисление среднего квадрата скорости молекул равновесного газа. Ответ этой задачи нам уже известен и получен, исходя из основного уравнения молекулярно-кинетической теории и определения температуры. Итак, средний квадрат скорости равен интегралу от нуля до бесконечности от произведения квадрата скорости на функцию распределения:
Интегрирование по частям последнего интеграла дает выражение для среднего квадрата скорости в виде
что находится в полном соответствии с выражением для средней квадратичной скорости, полученным из основного уравнения МКТ. Определим теперь по общему правилу нахождения средних значений выражение для средней скорости движения молекул идеального газа в состоянии термодинамического равновесия.
Для вычисления интеграла выполним замену переменной b º v2 тогда получим:
после интегрирования по частям и тождественных преобразований получаем
Таким образом, можно показать характерные скорости функции распределения Максвелла молекул по абсолютным значениям скорости, что представлено на рис. 1.7.1.
По описанной выше схеме можно найти выражения для средней относительной скорости, среднего квадрата относительной скорости, используя функцию распределения молекул по относительным скоростям (34). А так же определить вычисления средних значений квадрата скорости, относительной скорости, квадрата относительной скорости, кинетической энергии.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . (29)
. (29)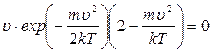 , (30)
, (30)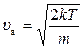 (31)
(31)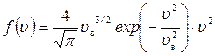 , (32)
, (32) равна
равна (33)
(33) - относительную скорость молекулы - и получим выражение для нахождения вероятности обнаружения у частицы относительной скорости в интервале
- относительную скорость молекулы - и получим выражение для нахождения вероятности обнаружения у частицы относительной скорости в интервале  :
: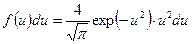 . (34)
. (34)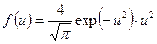 . (35)
. (35) . (36)
. (36)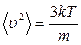 , (37)
, (37)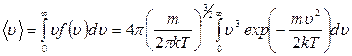 . (38)
. (38)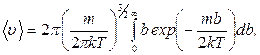 (39)
(39)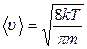 . (40)
. (40)
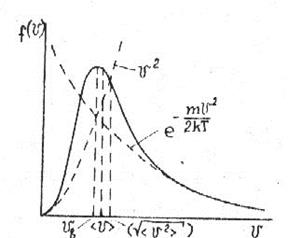 Средняя скорость и средний квадрат скорости молекул больше наивероятнейшей скорости. Это ясно из того, что функция распределения несимметрична, причем площадь под графиком функции распределения Максвелла слева от максимума меньше площади под графиком справа от максимума. Это означает, что доля молекул, имеющих скорости большие наивероятнейшей превосходит долю молекул, скорости которых меньше нее, а следовательно и средняя, и средняя квадратичная скорости больше наивероятнейшей.
Средняя скорость и средний квадрат скорости молекул больше наивероятнейшей скорости. Это ясно из того, что функция распределения несимметрична, причем площадь под графиком функции распределения Максвелла слева от максимума меньше площади под графиком справа от максимума. Это означает, что доля молекул, имеющих скорости большие наивероятнейшей превосходит долю молекул, скорости которых меньше нее, а следовательно и средняя, и средняя квадратичная скорости больше наивероятнейшей.