
|
|
Сети – классификаторы входных векторов
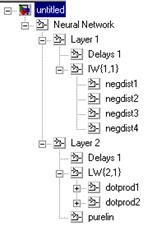
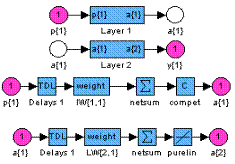
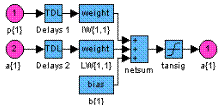
Синтаксис: net = newlvq(PR,S1,PC,LR,LF) Описание: Нейронные сети-классификаторы входных векторов, или сети LVQ, в отличие от самоорганизующихся сетей выполняют не только кластеризацию, но и классификацию входных векторов. Функция net = newlvq(PR, s1, PC, lr, lf) формирует сеть LVQ и имеет следующие входные и выходные аргументы. Входные аргументы: PR – массив размера R´2 из Q минимальных и максимальных значений вектора входа; s1 – число нейронов скрытого слоя; PC – вектор размера 1´S2, указывающий распределение по долям векторов каждого класса; lr – параметр скорости настройки, по умолчанию 0.01; lf – функция настройки, по умолчанию learnlv2. Выходные аргументы: net – объект класса network object, определяющий сеть-классификатор LVQ. Свойства сети: Сеть LVQ – это двухслойная сеть. Первый слой использует функции взвешивания negdist, накопления netsum и активации compet. Второй слой использует функции взвешивания dotprodt, накопления netsum и активации purelin. Слои не имеют смещений. Веса первого слоя инициализируются с помощью функции midpoint; веса второго слоя устанавливаются так, чтобы каждому нейрону на выходе соответствовал единственный нейрон скрытого слоя. Адаптация и обучение выполняются с помощью функций adaptwb Пример: Векторы входа P и выходные классы Tc, представленные ниже, определяют задачу классификации, которая будет решена LVQ-сетью: P = [–3 –2 –2 0 0 0 0 +2 +2 +3; 0 +1 –1 2 1 –1 –2 +1 –1 0]; Tc = [1 1 1 2 2 2 2 1 1 1]; Целевые классы Tc преобразуем в целевые векторы T, создадим сеть LVQ со входами P, четырьмя нейронами и долями распределения по классам [0.6 0.4]: T = ind2vec(Tc); net = newlvq(minmax(P),4,[.6 .4]); gensim(net) % Рис.11.32 Структура нейронной сети LVQ показана на рис. 11.32. Выполним обучение сети:
Рис. 11.32 net = train(net,P,T); Промоделируем сеть на векторе входа: Y = sim(net,P); Yc = vec2ind(Y) Yc = 1 1 1 2 2 2 2 1 1 1 Классификация входного вектора выполнена без ошибок. Сопутствующие функции: SIM, INIT, ADAPT, TRAIN, ADAPTWB, TRAINWB1, LEARNLV1, LEARNLV2. Рекуррентные сети
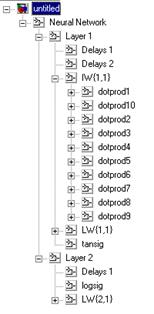
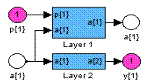
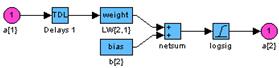
Сеть Элмана Синтаксис: net = newelm(PR, [S1 S2 ... SNl], {TF1 TF2 ... TFNl}, btf, blf, pf) Описание: Функция newelm предназначена для создания динамических сетей Элмана, которые применяются для построения моделей динамических систем. Функция net = newelm(PR, [S1 S2 ... SNl], {TF1 TF2 ... TFNl}, btf, blf, pf) формирует сеть Элмана и имеет следующие входные и выходные аргументы. Входные аргументы: PR – массив размера R´2 минимальных и максимальных значений для R векторов входа; Si – количество нейронов в слое i; TFi – функция активации слоя i, по умолчанию tansig; btf – обучающая функция, реализующая метод обратного распространения, по умолчанию traingdx; blf – функция настройки, реализующая метод обратного распространения, по умолчанию learngdm; pf – критерий качества обучения, по умолчанию mse. Выходные аргументы: net – объект класса network object динамической сети Элмана. Свойства сети: Обучающими функциями могут быть любые функции, реализующие метод обратного распространения: trainlm, trainbfg, trainrp, traingd и др. Функциями настройки могут быть функции, реализующие метод обратного распространения: learngd, learngdm. Критерием качества обучения может быть любая дифференцируемая функция: mse, msereg. При реализации сети Элмана не рекомендуется применять такие алгоритмы обучения, как trainlm или trainrp, которые работают с большим размером шага. Пример: Зададим вход P в виде случайной булевой последовательности из нулей и единиц; выходом сети должна быть такая булева последовательность T, элементы которой принимают значение 1 только в том случае, когда в последовательности P встретились 2 единицы подряд: P = round(rand(1,20)) T = [0 (P(1:end–1)+P(2:end)==2)] P = 1 0 1 0 1 1 0 0 1 0 1 1 1 1 0 0 1 1 0 1 T = 0 0 0 0 0 1 0 0 0 0 0 1 1 1 0 0 0 1 0 0 Требуется построить сеть, которая распознает во входном сигнале 2 единицы, следующие подряд. Сначала эти последовательности представим в виде массивов ячеек: Pseq = con2seq(P); Tseq = con2seq(T); Создадим сеть Элмана с диапазоном входного сигнала от 0 до 1 с 10 скрытыми и одним выходным нейронами (рис. 11.33): net = newelm([0 1],[10 1],{'tansig','logsig'}); gensim(net) % Рис.11.33
Рис. 11.33 Затем обучим сеть с допустимой средней квадратичной ошибкой 0.001 и смоделируем ее: net.trainParam.goal = 0.001; net.trainParam.epochs = 1000; net = train(net,Pseq,Tseq); Y = sim(net,Pseq) Y1 = seq2con(Y); E = round(T–Y1{1}) E = 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Результат свидетельствует о том, что сеть справилась с поставленной задачей. Алгоритм: Сеть Элмана состоит из Nl слоев, использующих функции взвешивания dotprod, накопления netsum и заданные пользователем функции активации. Все слои имеют смещения. Выход последнего слоя является выходом сети. Веса и смещения инициализируются Сопутствующие функции: NEWFF, NEWCF, SIM, INIT, ADAPT, TRAIN.
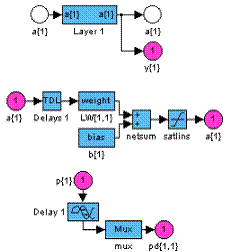
Синтаксис: net = newhop(T) Описание: Сети Хопфилда применяются для решения задач распознавания образов. Функция net = newhop(T) имеет 1 входной аргумент – массив T размера R´Q, объединяющий Q целевых векторов (со значениями +1 или –1), R – число элементов вектора входа. Функция возвращает рекуррентную сеть Хопфилда в виде объекта класса network object. Свойства: Сеть Хопфилда имеет 1 нейронный слой с функциями взвешивания dotprod, накопления netsum и активации satlins. Слой охвачен динамической обратной связью и имеет смещения. Пример: Создадим сеть Хопфилда с двумя устойчивыми точками в трехмерном пространстве: T = [–1 –1 1; 1 –1 1]'; net = newhop(T); gensim(net) % Рис.11.34
Рис. 11.34 Проверим, что сеть устойчива в этих точках, и используем их как начальные условия для линии задержки. Если сеть устойчива, можно ожидать, что выходы Y будут те же самые. Ai = T; [Y,Pf,Af] = sim(net,2,[],Ai); Y = –1 1 –1 –1 1 1 Таким образом, вершины гиперкуба являются устойчивыми точками равновесия сети Хопфилда. Проверим сходимость сети при произвольном входном векторе Ai: Ai = {[–0.9; –0.8; 0.7]}; [Y,Pf,Af] = sim(net,{1 5},{},Ai); Y{1} ans = –1 –1 Сеть Хопфилда обеспечила переход к устойчивому положению равновесия, ближайшему к заданному входу. Алгоритм: Сети Хопфилда разработаны для того, чтобы приводить случайные входные векторы к точкам равновесия, которые соответствуют определенным, заданным пользователем, целям. Алгоритм минимизирует число устойчивых паразитных точек равновесия [25]. Сопутствующие функции: sim, satlins. Функции активации Функция активации, или передаточная функция нейрона, преобразует каждый элемент ni вектора входа нейрона в элемент ai вектора выхода:
Если рассматривать слой нейронов, то выражение функции активации через параметры слоя может быть записано в следующей векторной форме:
где a m – вектор выхода нейронов размера S m´1 для слоя m; Wm – матрица весовых коэффициентов размера S m´ S m –1 для слоя m; bm – вектор смещений размера S m´1 для слоя m; f m – функция активации нейронов слоя m; nm – вектор входа нейронов для слоя m; Sm – число нейронов слоя m; a0 = p – вектор входа сети размера S0 ´1, причем S0 = R и R – число элементов вектора входа сети. Все М-функции ППП NNToolbox, описывающие функции активации, имеют одинаковый формат A = <имя_функции>(N), где A – матрица векторов выхода; N – матрица векторов входа. Производные функций активации имеют следующий формат dA_dN = d<имя_функции>(N,A). Кроме того, для функций активации определена информационная функция вида info = <имя_функции>(code), где аргумент code может принимать следующие значения: 'name' – полное название функции активации; 'deriv' – имя производной функции активации; 'active' – активный диапазон входа функции активации; 'output' – диапазон выхода функции активации. Персептрон
Блок Simulink:
Синтаксис:
Описание: Функция A = hardlim(N) реализует функцию активации с жесткими ограничениями, которая возвращает выход нейрона равным 1, если вход достигает порогового значения, Функция info = hardlim(code) сообщает информацию о функции hardlim. Функция dA_dN = dhardlim(N, A) вычисляет производную функции hardlim. Пример: Информация о функции активации hardlim: name = hardlim('name') dname = hardlim('deriv') inrange = hardlim('active') outrange = hardlim('output') name = Hard Limit dname = dhardlim inrange = 0 0 outrange = 0 1 Зададим следующий вектор входа функции активации с жесткими ограничениями для слоя из трех нейронов и рассчитаем вектор выхода A и производную dA_dN: N = [0.1; 0.8; –0.7];
Применение функции: Функция активации hardlim используется при формировании нейронной сети персептрона с помощью М-функции newp. Для задания функции активации hardlim следует Алгоритм: Функция активации hardlim и ее производная dhardlim определяются следующими
Сопутствующие функции: sim, hardlims.
Блок Simulink:
Синтаксис:
Описание: Функция A = hardlims(N) реализует симметричную функцию активации с жесткими ограничениями, которая возвращает выход нейрона равным 1 при положительном и –1 при отрицательном пороговом значении. Функция info = hardlims(code) сообщает информацию о функции hardlims. Функция dA_dN = dhardlms(N, A) вычисляет производную функции hardlims. Пример: Информация о функции активации hardlims: name = hardlims('name') dname = hardlims('deriv') inrange = hardlims('active') outrange = hardlims('output') name = Symmetric Hard Limit dname = dhardlms inrange = 0 0 outrange = –1 1 Зададим следующий вектор входа симметричной функции активации с жесткими ограничениями для слоя из трех нейронов и рассчитаем вектор выхода A и производную dA_dN: N = [0.1; 0.8; –0.7];
Применение функции: Функция активации hardlims используется при формировании нейронной сети персептрона с помощью М-функции newp. Для задания функции активации hardlims следует установить значение свойства net.layers{i}.transferFcn равным 'hardlims'. Алгоритм: Функция активации hardlims и ее производная dhardlms определяются следующими соотношениями:
Сопутствующие функции: sim, hardlim. Линейные сети
Блок Simulink:
Синтаксис:
Описание: Функция A = purelin(N) реализует линейную функцию активации во всем диапазоне изменения входного аргумента. Функция info = purelin(code) сообщает информацию о функции purelin. Функция dA_dN = dpurelin(N, A) вычисляет производную функции purelin. Пример: Информация о функции активации purelin: name = purelin('name') dname = purelin('deriv') inrange = purelin('active') outrange = purelin('output') name = Linear dname = dpurelin inrange = –Inf Inf outrange = –Inf Inf Зададим следующий вектор входа линейной функции активации для слоя из трех нейронов и рассчитаем вектор выхода A и производную dA_dN: N = [0.1; 0.8; –0.7];
Применение функции: Функция активации purelin используется при формировании нейронных сетей Алгоритм: Функция активации purelin и ее производная dpurelin определяются следующими
Сопутствующие функции: sim, satlin, satlins.
Блок Simulink:
Синтаксис:
Описание: Функция A = poslin(N) реализует положительную линейную функцию активации. Функция info = poslin(code) сообщает информацию о функции poslin. Функция dA_dN = dposlin(N, A) вычисляет производную функции poslin. Пример: Информация о функции активации poslin: name = poslin('name') dname = poslin('deriv') inrange = poslin('active') outrange = poslin('output') name = Positive Linear dname = dposlin inrange = 0 Inf outrange = 0 Inf Зададим следующий вектор входа положительной линейной функции активации N = [0.1; 0.8; –0.7];
Применение функции: Для задания функции активации poslin следует установить значение свойства net.layers{i}.transferFcn равным 'poslin'. Алгоритм: Функция активации poslin и ее производная dposlin определяются следующими
Сопутствующие функции: SIM, PURELIN, SATLIN, SATLINS.
Блок Simulink:
Синтаксис:
Описание: Функция A = satlin(N) реализует линейную функцию активации с ограничениями. Функция info = satlin(code) сообщает информацию о функции satlin. Функция dA_dN = dsatlin(N, A) вычисляет производную функции satlin. Пример: Информация о функции активации satlin: name = satlin('name') dname = satlin('deriv') inrange = satlin('active') outrange = satlin('output') name = Saturating Linear dname = dsatlin inrange = 0 1 outrange = 0 1 Зададим следующий вектор входа линейной функции активации с ограничениями N = [0.1; 0.8; –0.7];
Применение функции: Для задания функции активации satlin следует установить значение свойства net.layers{i}.transferFcn равным 'satlin'. Алгоритм: Функция активации satlin и ее производная dsatlin определяются следующими
Сопутствующие функции: SIM, POSLIN, SATLINS, PURELINS.
Блок Simulink:
Синтаксис:
Описание: Функция A = satlins(N) реализует симметричную линейную функцию активации Функция info = satlins(code) сообщает информацию о функции satlins. Функция dA_dN = dsatlins(N, A) вычисляет производную функции satlins. Пример: Информация о функции активации satlins: name = satlins('name') dname = satlins('deriv') inrange = satlins('active') outrange = satlins('output') name = Symmetric Saturating Linear dname = dsatlins inrange = –1 1 outrange = –1 1 Зададим следующий вектор входа симметричной линейной функции активации N = [0.1; 0.8; –0.7];
Применение функции: Для задания функции активации satlins следует установить значение свойства net.layers{i}.transferFcn равным 'satlins'. Алгоритм: Функция активации satlins и ее производная dsatlins определяются следующими
Сопутствующие функции: SIM, POSLIN, SATLIN, PURELINS. Радиальные базисные сети
Блок Simulink:
Синтаксис:
Описание: Функция A = radbas(N) реализует радиальную базисную функцию активации. Функция info = radbas(code) сообщает информацию о функции radbas. Функция dA_dN = dradbas(N, A) вычисляет производную функции radbas. Пример: Информация о функции активации radbas: name = radbas('name') dname = radbas('deriv') inrange = radbas('active') outrange = radbas('output') name = Radial Basis dname = dradbas inrange = –2 2 outrange = 0 1 Следующая последовательность команд создает график функции активации radbas: n = –3:0.1:3; a = radbas(n); plot(n,a) % Рис.11.35
Зададим следующий вектор входа радиальной базисной функции активации для слоя из трех нейронов и рассчитаем вектор выхода A и производную dA_dN: N = [0.1; 0.8; –0.7];
Применение функции: Функция активации radbas используется при формировании вероятностных и обобщенных регрессионных сетей с помощью М-функций newpnn и newgrnn. Для задания функции активации radbas следует установить значение свойства net.layers{i}.transferFcn равным 'radbas'. Алгоритм: Функция активации radbas и ее производная dradbas определяются следующими
Сопутствующие функции: sim, tribas, dradbas.
Блок Simulink:
Синтаксис:
Описание: Функция A = tribas(N) реализует треугольную функцию активации. Функция info = tribas(code) сообщает информацию о функции tribas. Функция dA_dN = dtribas(N, A) вычисляет производную функции tribas. Пример: Информация о функции активации tribas: name = tribas('name') dname = tribas('deriv') inrange = tribas('active') outrange = tribas('output') name = Triangle Basis dname = dtribas inrange = –1 1 outrange = 0 1 Построим график функции активации tribas (рис. 11.36): n = –2:0.1:2; a = tribas(n); plot(n,a) % Рис.11.36
Зададим следующий вектор входа треугольной функции активации для слоя из трех нейронов и рассчитаем вектор выхода A и производную dA_dN: N = [0.1; 0.8; –0.7];
Применение функции: Для задания функции активации tribas следует установить значение свойства net.layers{i}.transferFcn равным 'tribas'. Алгоритм: Функция активации tribas и ее производная dtribas определяются следующими
Сопутствующие функции: SIM, RADBAS. Самоорганизующиеся сети
Блок Simulink:
Синтаксис: A = compet(N) info = compet(code) Описание: Функция A = compet(N) реализует конкурирующую функцию активации. Функция info = compet(code) сообщает информацию о функции compet. Функция compet не имеет производной. Конкурирующая функция преобразует вектор входа слоя нейронов так, чтобы нейрон с самым большим входом имел выход, равный 1, а всего другие нейроны имели выходы, равные 0. Пример: Информация о функции активации compet: name = compet('name') dname = compet('deriv') inrange = compet('active') outrange = compet('output') name = Competitive dname = '' inrange = –Inf Inf outrange = 0 1 Зададим следующий вектор входа конкурирующей функции активации, вычислим выход и представим входы и выходы в виде столбцовых диаграмм (рис. 11.37): n = [0; 1; –0.5; 0.5]; a = compet(n); subplot(2,1,1), bar(n), ylabel('n') subplot(2,1,2), bar(a), ylabel('a') % Рис.11.37
Применение функции: Функция активации compet используется при формировании вероятностных и самоорганизующихся нейронных сетей с помощью М-функций newc и newpnn. Для задания функции активации compet следует установить значение свойства net.layers{i}.transferFcn равным 'compet'. Сопутствующие функции: SIM, SOFTMAX.
Блок Simulink:
Синтаксис: A = softmax(N) info = softmax(code) Описание: Функция A = softmax(N) реализует конкурирующую функцию активации с мягким максимумом. Функция info = softmax(code) сообщает информацию о функции softmax. Функция softmax не имеет производной. Пример: Информация о функции активации softmax: name = softmax('name') dname = softmax('deriv') inrange = softmax('active') outrange = softmax('output') name = Soft Max dname = '' inrange = –Inf Inf outrange = 0 1 Зададим следующий вектор входа конкурирующей функции активации с мягким максимумом, вычислим выход и представим входы и выходы в виде столбцовых диаграмм: n = [0; 1; –0.5; 0.5]; a = softmax(n); subplot(2,1,1), bar(n), ylabel('n') subplot(2,1,2), bar(a), ylabel('a') % Рис.11.38
Применение функции: Функция активации softmax используется при формировании вероятностных и самоорганизующихся нейронных сетей с помощью М-функций newc и newpnn. Для задания функции активации softmax следует установить значение свойства net.layers{i}.transferFcn равным 'softmax'. Сопутствующие функции: sim, compet. Рекуррентные сети
Блок Simulink:
Синтаксис:
Описание: Функция A = logsig(N) реализует логистическую сигмоидальную функцию активации. Функция info = logsig(code) сообщает информацию о функции logsig. Функция dA_dN = logsig(N, A) вычисляет производную функции logsig. Пример: Информация о функции активации logsig: name = logsig('name') dname = logsig('deriv') inrange = logsig('active') outrange = logsig('output') name = Log Sigmoid dname = dlogsig inrange = –4 4 outrange = 0 1 Построим график функции активации logsig(рис. 11.39): n = –5:0.1:5; a = logsig(n); plot(n,a) % Рис.11.39
Зададим следующий вектор входа логистической функции активации для слоя из трех нейронов и рассчитаем вектор выхода A и производную dA_dN: N = [0.1; 0.8; –0.7];
Применение функции: Функция активации logsig используется при формировании нейронных сетей прямой передачи с помощью М-функций newff и newcf. Для задания функции активации logsig следует установить значение свойства net.layers{i}.transferFcn равным 'logsig'. Алгоритм: Функция активации logsig и ее производная dlogsig определяются следующими
Сопутствующие функции: sim, dlogsig, dtansig.
Блок Simulink:
Синтаксис:
Описание: Функция A = tansig(N) реализует гиперболическую тангенциальную функцию активации. Функция info = tansig(code) сообщает информацию о функции tansig. Функция dA_dN = tansig(N, A) вычисляет производную функции tansig. Пример: Информация о функции активации tansig: name = tansig('name') dname = tansig('deriv') inrange = tansig('active') outrange = tansig('output') name = Tan Sigmoid dname = dtansig inrange = –2 2 outrange = –1 1 Следующая последовательность команд строит график функции активации tansig: n = –3:0.1:3; a = tansig(n); plot(n,a) % Рис.11.40
Зададим следующий вектор входа гиперболической тангенциальной функции активации для слоя из трех нейронов и рассчитаем вектор выхода A и производную dA_dN: N = [0.1; 0.8; –0.7];
Применение функции: Функция активации tansig используется при формировании нейронных сетей прямой передачи с помощью М-функций newff и newcf. Для задания функции активации tansig следует установить значение свойства net.layers{i}.transferFcn равным 'tansig'. Алгоритм: Функция активации tansig и ее производная dtansig определяются следующими
Приведенное выражение для функции tansig(n) математически эквивалентно функции tanh(N), но отличается тем, что выполняется быстрее, чем реализация функции tanh в системе MATLAB. Для нейронных сетей, где быстродействие играет важную роль, это весьма существенно [42]. Сопутствующие функции: sim, dtansig, logsig. Синаптические функции Функции этой группы выполняют следующие операции над векторами входов нейронной сети: взвешивание, вычисление расстояний в сетях с топологией, накопление для вычисления потенциала нейрона. При описании синаптических функций описывается 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
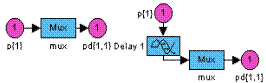

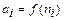 .
.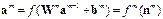 ,
,
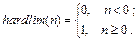
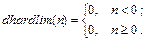

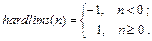
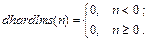

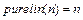 ;
;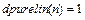 .
.
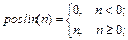
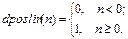

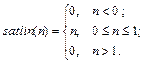
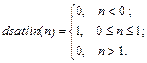
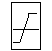
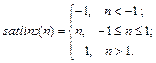
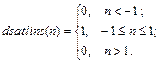

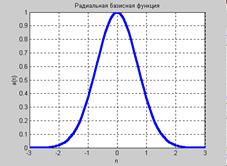 Рис. 11.35
Рис. 11.35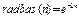 ;
;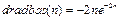 .
.
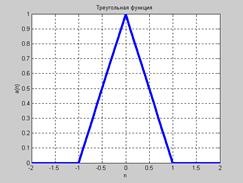 Рис. 11.36
Рис. 11.36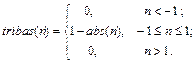
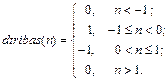 ;
;
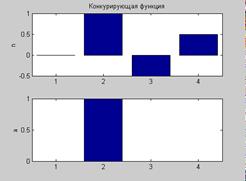 Рис. 11.37
Рис. 11.37
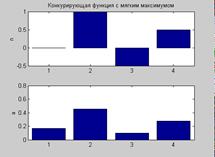 Рис. 11.38
Рис. 11.38
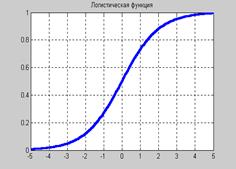 Рис. 11.39
Рис. 11.39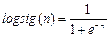 ;
;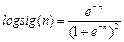 .
.
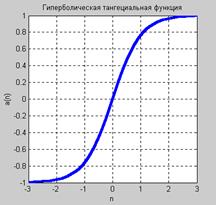 Рис. 11.40
Рис. 11.40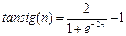 ;
;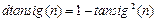 .
.