
|
|
Регулятор с предсказаниемРегулятор с предсказанием, реализованный в ППП Neural Network Toolbox, использует модель нелинейного управляемого процесса в виде нейронной сети для того, чтобы предсказывать его будущее поведение. Кроме того, регулятор вычисляет сигнал управления, который оптимизирует поведение объекта на заданном интервале времени. Идентификация управляемого процесса. Схема подсистемы идентификации показана на рис. 9.29. Она включает модель управляемого процесса в виде нейронной сети, которая должна быть обучена в автономном режиме так, чтобы минимизировать ошибку между реакциями процесса и модели e = yp – ym на последовательность пробных сигналов u.
Нейронная сеть регулятора управляемого процесса представлена на рис. 9.30; она име-
Настройка параметров этой сети выполняется автономно методом группового обучения, используя данные, полученные при испытаниях реального объекта. Для обучения сети может быть использован любой из обучающих алгоритмов для нейронных сетей. Принцип управления с предсказанием. Управление с предсказанием использует принцип удаляющегося горизонта [40], когда нейросетевая модель управляемого процесса предсказывает реакцию объекта управления на определенном интервале времени в будущем. Предсказания используются программой численной оптимизации для того, чтобы вычислить управляющий сигнал, который минимизирует следующий критерий качества управления:
где константы N1, N2 и Nu задают пределы, внутри которых вычисляются ошибка слежения и мощность управляющего сигнала. Переменная u' описывает пробный управляющий сигнал, yr – желаемая, а ym – истинная реакция модели управляемого процесса. Величина r определяет вклад, который вносит мощность управления в критерий качества. Структурная схема на рис. 9.31 иллюстрирует процесс управления с предсказанием. Регулятор состоит из нейросетевой модели управляемого процесса и блока оптимизации. Блок оптимизации определяет значения u', которые минимизируют критерий качества управления, а соответствующий управляющий сигнал управляет процессом.
Реализация регулятора с предсказанием. В качестве примера исследуется процесс управления каталитическим реактором с непрерывным перемешиванием (Continous Stirred Tank Reactor – CSTR), схема которого показана на рис. 9.32.
Динамическая модель управляемого процесса описывается следующими обыкновенными нелинейными дифференциальными уравнениями:
где h – уровень жидкости в резервуаре; w1(t) – скорость потока продукта с концентрацией Cb1; w2(t) – скорость потока разбавленного продукта с концентрацией Cb2; Cb – концентрация продукта на выходе объекта. Исходные концентрации приняты равными Cb1 = 29.4 и Cb2 = 0.1. Константы скорости расхода равны k1 = k2 = 1. Цель регулирования состоит в поддержании концентрации продукта путем регулирования скорости потока w2(t). Для простоты принято w1(t) = 0.1. В этом примере уровень раствора в резервуаре не регулируется. Нелинейная динамическая модель каталитического реактора, соответствующая уравнениям (9.5), показана на рис. 9.33
Рис. 9.33 Чтобы разобрать этот достаточно сложный демонстрационный пример, следует Описываемые ниже приложения нейронных сетей реализованы только в рамках MAT-файлы данных: cstr1, cstr2, cstr3 – данные для обучения нейросетевой модели каталитического реактора. Функции одномерной оптимизации: csrchbac – поиск с обратной прогонкой; csrchbre – метод Брента (Brent), объединяющий методы золотого сечения и квадратичной интерполяции; csrchcha – метод кубической интерполяции Чараламбуса; csrchgol – метод золотого сечения; csrchhyb – гибридный метод бисекции и кубической интерполяции. Функции для синтеза управления с предсказанием: calcjjdjj – вычисление функционала качества и его градиента; predopt – оптимизация регулятора с предсказанием; dyduvar – вычисление частных производных выхода по входу. Модели Simulink: cstr – модель каталитического реактора; predcstr – GUI-приложение для контроллера с предсказанием; ptest3sim2 – нейросетевая модель управляемого процесса, используемая М-функцией predopt для предсказания процесса в будущем. Вспомогательные функции: sfunxy2 – S-функция для вывода графиков; nncontrolutil – поддержка, обеспечивающая возможность обращения к частным Выполнить запуск демонстрационного примера можно несколькими способами: · в окне запуска приложений Launch Pad выбрать опцию Demos для ППП Neural Network Toolbox; · ввести команду predcstr, используя командное окно системы MATLAB. В любом случае открывается окно системы Simulink со следующей структурой системы управления (рис. 9.34).
Рис. 9.34 Эта структура включает блок управляемого процесса Plant и блок контроллера NN Predictive Controller, а также блоки генерации эталонного ступенчатого сигнала со случайной амплитудой Random Reference, отсчета времени Clock, построения графиков Graph. Особенность этой структуры заключается в том, что она выполняет не только функции блок-схемы системы Simulink, но и функции графического интерфейса пользователя GUI [53]. Для того чтобы начать работу, необходимо активизировать блок NN Predictive Controller двойным щелчком левой кнопки мыши. Появится окно, показанное на рис. 9.35.
Оно выполняет функции графического интерфейса пользователя. Обратите внимание на информацию, которая руководит вашими действиями и указана в области фрейма Вид окна Plant Identification приведен на рис. 9.36. Это окно универсально и может быть использовано для построения нейросетевых моделей для любого динамического объекта, который описан моделью Simulink. В рассматриваемом случае такой моделью является нелинейная динамическая модель каталитического реактора CSTR. Процедура идентификации позволяет построить нейронную сеть, которая будет моделировать динамику управляемого процесса. Если модель должна использоваться при настройке контроллера, то ее следует создать прежде, чем начнется расчет контроллера. Кроме того, вам может потребоваться создание новой модели объекта, если спроектированный контроллер будет функционировать неудовлетворительно.
Процедура идентификации требует задания следующих параметров: · параметры архитектуры: Size of the Hidden Layer. Размер скрытого слоя определяется количеством используемых нейронов; Sampling Interval. Такт дискретности в секундах определяет интервал между двумя последовательными моментами съема данных; No. Delayed Plant Inputs. Количество элементов запаздывания на входе модели; No. Delayed Plant Outputs. Количество элементов запаздывания на выходе модели; Normalize Training Data. Окно контроля нормирования обучающих данных к диапазону [0 1]; · параметры обучающей последовательности: Training samples. Длина обучающей выборки (количество точек съема информации); Maximum Plant Input. Максимальное значение входного сигнала; Minimum Plant Input. Минимальное значение входного сигнала; Maximum Interval Value (sec). Максимальный интервал идентификации в секундах; Minimum Interval Value (sec). Минимальный интервал идентификации в секундах; Limit Output Data. Окно контроля, позволяющее ограничить объем выходных данных; только при включенном окне контроля будут доступны 2 следующих окна редактирования текста; Maximum Plant Output. Максимальное значение выходного сигнала; Minimum Plant Input. Минимальное значение выходного сигнала; Simulink Plant Model. Задание модели Simulink с указанием входных и выходных портов, используемых при построении нейросетевой модели управляемого процесса. С помощью кнопки Browse вы можете выбрать любую модель из числа доступных; Generate Training Data. Кнопка запуска процесса генерации обучающей последовательности; Import Data. Импорт обучающей последовательности из рабочей области или файла данных. Для рассматриваемого примера эти данные накоплены в MAT-файлах cstr1, cstr2, cstr3; Export Data. Экспорт сгенерированных данных в рабочую область или MAT-файл; · параметры обучения: Training Epochs. Количество циклов обучения; Training function. Задание обучающей функции; Use Current Weights. Окно контроля, позволяющее подтвердить использование Use Validation/Testing for Training. Выбор этих окон контроля будет означать, что по 25 % данных из обучающей последовательности будет использовано для формирования контрольного и тестового подмножеств соответственно. Итак, выбор процедуры Generate Training Data приведет к тому, что будет запущена программа генерации обучающей последовательности на интервале 1600 с для модели каталитического реактора cstr.mdl. Программа генерирует обучающие данные путем воздействия ряда случайных ступенчатых сигналов на модель Simulink управляемого процесса. Графики входного и выходного сигналов объекта управления выводятся на экран (рис. 9.37).
По завершении генерации обучающей последовательности пользователю предлагается либо принять сгенерированные данные (Accept Data), либо отказаться от них (Reject Data). Если вы принимаете данные, приложение возвращает вас к несколько измененному окну Plant Identification(рис. 9.38). Здесь часть окон недоступны, а кнопка Generate Training Data заменена на кнопку Erase Generated Data, что позволяет удалить сгенерированные данные.
В окне фрейма содержится сообщение Обучающая последовательность состоит из 8000 замеров. Можно начинать обучение нейронной сети. Для этого следует воспользоваться кнопкой Train Network (Обучить сеть). Начнется обучение нейросетевой модели. После завершения обучения его результаты отображаются на графиках, как это показано на рис. 9.39, а и б, где построены соответственно результаты обучения и тестирования на контрольном множестве.
Рис. 9.39 Текущее состояние отмечено в окне Plant Identification(рис. 9.40) сообщением Обучение завершено. Вы можете сгенерировать или импортировать новые данные, продолжить обучение или сохранить полученные результаты, выбрав кнопки OK или Apply.
После этого мы вновь возвращаемся к окну Neural Network Predictive Control Cost Horizon (N2). Верхний предел суммирования в показателе качества N2 = 7, нижний предел N1 фиксирован и равен 1; Control Horizon (Nu). Верхний предел суммирования при оценке мощности управления Nu = 2; Control Weighting Factor (r). Коэффициент веса для составляющей мощности управления r = 0.05; Search parameter (a). Параметр одномерного поиска, задающий порог уменьшения показателя качества, a = 0.001; Minimization Routine. Выбор процедуры одномерного поиска; выбрана процедура csrchbac; Iterations Per Sample Time. Число итераций на 1 такт дискретности равно 2. Как только параметры оптимизации установлены, следует подтвердить это нажатием кнопок OK или Apply. В результате параметры регулятора будут введены в блок NN Predictive Controller системы Simulink. Возвращаемся к модели Simulink (рис. 9.34) и начинаем моделирование, выбрав
Из анализа полученных данных следует, что реакция системы на ступенчатые воздействия со случайной амплитудой вполне удовлетворительна, имеет колебательный характер с достаточно быстрым затуханием; на интервале 20 с все воздействия эффективно отрабатываются. Таким образом, регулятор с предсказанием, реализованный в виде нейронной сети, можно использовать для управления каталитическим реактором с непрерывным перемешиванием. Регулятор NARMA-L2 Нейросетевой регулятор, описанный в этом разделе, использует в качестве модели управляемого процесса модель нелинейной авторегрессии со скользящим средним (Nonlinear Autoregressive-Moving Average – NARMA-L2). Схема демонстрационного примера управления магнитной подушкой показана на рис. 9.42.
Рис. 9.42 Окно Model Browser в левой части рисунка содержит перечень всех блоков, входящих в состав системы управления, представленной в виде модели системы Simulink. Управляемым объектом является магнит, который движется только в вертикальном направлении в электромагнитном поле, как это схематично показано на рис. 9.43.
Уравнение движения этой системы имеет вид:
где y(t) – расстояние движущегося магнита от электромагнита; g – ускорение силы тяжести; a – постоянная магнитного поля, зависящая от числа витков обмотки и намагниченности электромагнита; i(t) – управляющий ток электромагнита; M – масса магнита; Соответствующая динамическая модель, реализованная в системе Simulink, показана на рис. 9.44. Точно такую же модель, но с конкретными числовыми данными вы сможете увидеть на экране терминала, если активизируете блок Plant (Magnet Levitation) в окне Model Browser.
Заметим, что рассматриваемая динамическая система является нелинейной, и мы будем строить ее дискретную нелинейную модель как авторегрессионную модель со скользящим средним, или NARMA-модель, в форме
где y(k) – выход модели; d – число тактов предсказания; u(k) – вход модели. На этапе идентификации необходимо построить нейронную сеть для NARMA-модели вида (9.7). Эта процедура аналогична описанной выше процедуре идентификации для регулятора с предсказанием. Если требуется спроектировать следящую систему, которая обеспечивает движение по заданной траектории y(k+d) = yr(k+d), (9.8) то это означает, что необходимо сформировать нелинейный регулятор следующего
Хотя такой регулятор с помощью нейронной сети и может быть сформирован, однако
Преимущество этой формы состоит в том, что теперь текущее управление можно
Непосредственное применение этого соотношения для реализации регулятора затруднительно, поскольку управление u(k) зависит от текущего значения выхода y(k). Поэтому управление (9.11) модифицируется следующим образом:
но при этом параметр предсказания должен удовлетворять условию d ³ 2. На рис. 9.45 показана структура соответствующего регулятора в виде нейронной сети.
Здесь следует обратить внимание на участки сети, которые выполняют аппроксимацию нелинейных операторов g и f в виде выходов Общая структурная схема системы с регулятором NARMA-L2 показана на рис. 9.46.
На схеме явным образом выделена эталонная модель, которая задает желаемую траекторию для выхода управляемого процесса. Демонстрационный пример NARMA-L2 Controller использует следующие файлы, размещенные в каталоге toolbox\nnet\nncontrol. MAT-файлы данных: ball1– данные для обучения нейросетевой модели магнитной подушки. Функции активации, используемые в нейронной сети контроллера NARMA-L2: netinv – функция активации (1/n); dnetinv – производная функции активации (1/n). Модели Simulink: ballrepel0 – модель магнитной подушки; narmamaglev – GUI-приложение для контроллера NARMA-L2. Вспомогательные функции: sfunxy2 – S-функция для вывода графиков; nncontrolutil – утилита, обеспечивающая возможность обращения к частным функциям из системы Simulink. Выполнить запуск демонстрационного примера можно несколькими способами: · в окне запуска приложений Launch Pad выбрать опцию Demos для ППП Neural Network Toolbox; · ввести команду narmamaglev в командном окне системы MATLAB. Для того чтобы начать работу, необходимо активизировать блок NARMA-L2 Controller двойным щелчком левой кнопки мыши. Появится окно, показанное на рис. 9.47.
Обратите внимание, что это окно дает возможность обучить модель NARMA-L2. Это окно работает так же, как и другие окна идентификации объекта управления, поэтому повторно подробно процесс обучения рассматривать не будем. После окончания обучения нажать на клавишу OKдляввода данных регулятора в модельSimulink.Возвращаемся к модели Simulink (см. рис. 9.34) и начинаем моделирование, выбрав опцию Start из меню Simulation. Графики задающего сигнала и выхода системы приведены на рис. 9.48.
Из анализа полученных данных следует, что реакция системы на ступенчатые воздействия со случайной амплитудой вполне удовлетворительна, имеет колебательный характер с достаточно быстрым затуханием; на интервале 5 с все уставки эффективно отрабатываются. Таким образом, регулятор NARMA-L2, реализованный в виде нейронной сети, можно использовать для управления магнитной подушкой. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Рис. 9.29
Рис. 9.29 Рис. 9.30
Рис. 9.30 , (9.4)
, (9.4) Рис. 9.31
Рис. 9.31 Рис. 9.32
Рис. 9.32 (9.5)
(9.5)
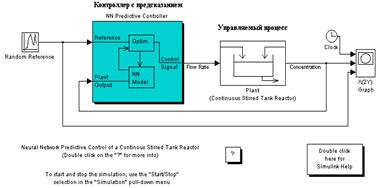
 Рис. 9.35
Рис. 9.35 Рис. 9.36
Рис. 9.36 Рис. 9.37
Рис. 9.37 Рис. 9.38
Рис. 9.38 а
а
 б
б
 Рис. 9.40
Рис. 9.40 Рис. 9.41
Рис. 9.41

 Рис. 9.43
Рис. 9.43 (9.6)
(9.6) Рис. 9.44
Рис. 9.44 , (9.7)
, (9.7) . (9.9)
. (9.9) (9.10)
(9.10) . (9.11)
. (9.11)
 , (9.12)
, (9.12) Рис. 9.45
Рис. 9.45 и
и  . Входами регулятора являются сигналы y(t+1) и u(t+1), последний реализован в виде обратной связи,
. Входами регулятора являются сигналы y(t+1) и u(t+1), последний реализован в виде обратной связи,  Рис. 9.46
Рис. 9.46 Рис. 9.47
Рис. 9.47 Рис. 9.48
Рис. 9.48