
|
|
Функции взвешивания и расстояний
Блок SIMULINK:
Синтаксис:
Описание: Функция Z = dotprod(W, P) вычисляет матрицу взвешенных входов в виде произведения W*P массива входов P размера R´Q и матрицы весов W размера S´R. Результатом является матрица Z размера S´Q. Функция df = dotprod('deriv') возвращает имя М-функции, которая вычисляет производную скалярного произведения по одному из сомножителей. Функции dZ_dP = ddotprod('p', W, P, Z) и dZ_dW = ddotprod('w', W, P, Z) имеют следующие входные и выходные аргументы: W – матрица весов размера S´R; P – массив входов размера R´Q; Z – матрица размера S´Q, где S – число нейронов в слое, Q – число векторов входа, dZ_dP – матрица производной dZ/dP размера S´R; dZ_dW – матрица производной dZ/dW размера R´Q. Примеры: Вычислим вектор взвешенных входов Z, если заданы случайные матрица весов W W = rand(4,3) P = rand(3,1); P' Z = dotprod(W,P); Z' W = 0.6068 0.4565 0.6154 0.4860 0.0185 0.7919 0.8913 0.8214 0.9218 0.7621 0.4447 0.7382 ans = 0.1763 0.4057 0.9355 ans = 0.8679 0.8340 1.3527 1.0053 Определим имя М-функции, которая вычисляет производную взвешенной функции df = dotprod('deriv') df = ddotprod Вычислим производные скалярного произведения по каждому аргументу: dZ_dP = ddotprod('p',W,P,Z) dZ_dW = ddotprod('w',W,P,Z) dZ_dP = 0.6068 0.4565 0.6154 0.4860 0.0185 0.7919 0.8913 0.8214 0.9218 0.7621 0.4447 0.7382 dZ_dW = 0.1763 0.4057 0.9355 Нетрудно убедиться, что производная произведения матрицы весов на вектор входа Применение функции: Функция взвешивания dotprod используется по умолчанию при формировании нейронных сетей персептрона newp и линейных слоев newlin. Чтобы применить эту функцию для формирования других типов сетей необходимо установить значения свойств net.inputWeight{i, j}.weightFcn и net.layerWeight{i, j}.weightFcn равными 'dotprod'. Алгоритм: Производная скалярного произведения двух матриц Z = W*P по одной из них равна второй матрице, т. е. dZ/dP = W, dZ/dW = P. Сопутствующие функции: SIM, DIST, NEGDIST, NORMPROD.
Синтаксис:
Описание: Функция взвешивания normprod отличается от функции dotprod тем, что она является нормированной функцией и не имеет производной. Функция Z = normprod(W,P) вычисляет массив взвешенных входов в виде нормированного скалярного произведения W*P/sum(P,1), где W – матрица весов размера S´R, Функция df = normprod('deriv') возвращает пустую строку ' ', так как производная Пример: Определим случайную весовую матрицу W и вектор входа P и рассчитаем соответствующий взвешенный вход Z: W = rand(4,3) P = rand(3,1); P' Z = normprod(W,P); Z' W = 0.0153 0.4660 0.2026 0.7468 0.4186 0.6721 0.4451 0.8462 0.8381 0.9318 0.5252 0.0196 ans = 0.6813 0.3795 0.8318 ans = 0.1880 0.6482 0.6983 0.4494 Применение функции: Функция взвешивания normprod применяется в архитектуре обобщенных регрессионных сетей, формируемых с помощью М-функции newgrnn. Чтобы применить функцию взвешивания normprod, следует установить значения Алгоритм: Функция normprod возвращает скалярные произведения весовой матрицы на каждый вектор входа, деленные на сумму элементов каждого вектора, в виде следующей матрицы Z: Z = W*P./sum(P, 1). Сопутствующие функции: SIM, DOTPROD, NEGDIST, DIST. Функции расстояний могут использоваться как функции взвешивания, но их основное назначение характеризовать топологию вероятностных и самоорганизующихся сетей путем вычисления расстояний между нейронами в слое.
Блок SIMULINK:
Синтаксис:
Описание: Функция взвешивания Z = dist(W, P) вычисляет евклидово расстояние между каждой строкой wi матрицы весов W и каждым столбцом pj матрицы входов P в соответствии zij = norm(wi – pj'). (11.1) Функция Z = dist(W, P) вычисляет матрицу взвешенных входов для матрицы входов Pразмера R´Q и матрицы весов W размера S´R. Результатом является матрица Z размера S´Q. Функция df = dist('deriv') возвращает пустую строку, поскольку производная не определена. Функция dist может быть использована как функция для вычисления расстояний Функция расстояния D = dist(pos) вычисляет расстояние между нейронами для сетей Примеры: Вычислим вектор взвешенных входов Z, если заданы случайные матрица весов W размера 4´3 и вектор входа P размера 3´1: W = rand(4,3); P = rand(3,1); Z = dist(W,P) Z = 0.6791 0.3994 0.3234 0.5746 Результатом является вектор размера 4´1, вычисленный в соответствии с соотношением (11.1). Рассмотрим сеть с топологией, для которой задана случайная матрица координат pos = rand(3,10); D = dist(pos) D = Columns 1 through 7 0 0.5304 0.9195 0.9366 0.5776 1.0651 0.9003 0.5304 0 0.7033 0.4450 0.7648 1.1121 0.8339 0.9195 0.7033 0 0.5551 0.6438 0.7713 0.3219 0.9366 0.4450 0.5551 0 0.9521 1.1444 0.7971 0.5776 0.7648 0.6438 0.9521 0 0.9396 0.6349 1.0651 1.1121 0.7713 1.1444 0.9396 0 0.4624 0.9003 0.8339 0.3219 0.7971 0.6349 0.4624 0 1.1471 0.9753 0.4052 0.8125 0.9155 0.5243 0.2948 0.3750 0.2967 0.6520 0.6215 0.6276 0.8666 0.6631 1.0744 0.9119 0.4235 0.7844 0.8969 0.4576 0.2754 Columns 8 through 10 1.1471 0.3750 1.0744 0.9753 0.2967 0.9119 0.4052 0.6520 0.4235 0.8125 0.6215 0.7844 0.9155 0.6276 0.8969 0.5243 0.8666 0.4576 0.2948 0.6631 0.2754 0 0.8512 0.1166 0.8512 0 0.7709 0.1166 0.7709 0 В результате получаем симметричную матрицу взаимных расстояний между нейронами. Применение функции: Функция взвешивания dist используется при формировании вероятностных сетей newpnn и обобщенных регрессионных сетей newgrnn. Чтобы применить эту функцию взвешивания для формирования других типов сетей необходимо установить значения свойств net.inputWeight{i, j}.weightFcn и net.layerWeight{i, j}.weightFcn равными 'dist'. Чтобы применить функцию расстояния dist для сетей с топологией, необходимо установить значение свойства net.layers{i}.distanceFcn равным 'dist'. Алгоритм: Евклидово расстояние d между векторами x и y вычисляется в системе MATLAB d = sqrt((x–y).^2). Сопутствующие функции: SIM, DOTPROD, NEGDIST, NORMPROD, MANDIST, LINKDIST.
Синтаксис: Z = negdist(W, P) df = negdist('deriv') Описание: Функция negdist применяется в самоорганизующихся сетях как функция взвешивания. Функция взвешивания Z = negdist(W, P) вычисляет отрицательное евклидово расстояние между каждой строкой wi матрицы весов W и каждым столбцом pj матрицы входов P в соответствии со следующим соотношением: zij = norm(wi – pj'). (11.2) Функция Z = dist(W, P) вычисляет матрицу взвешенных входов для матрицы входов P размера R´Q и матрицы весов W размера S´R. Результатом является матрица Z размера S´Q. Функция df = dist('deriv') возвращает пустую строку, поскольку производная не определена. Пример: Вычислим вектор взвешенных входов Z, если заданы случайные матрица весов Wразмера 4´3 и вектор входа P размера 3´1: W = rand(4,3); P = rand(3,1); Z = negdist(W,P) Z = –0.7558 –0.8090 –0.4755 –0.8113 Применение функции: Функция взвешивания negdist используется при формировании самоорганизующихся сетей newc и newsom. Чтобы применить эту функцию взвешивания для других сетей, необходимо установить значения свойств net.inputWeight{i, j}.weightFcn и net.layerWeight{i, j}.weightFcn равными 'negdist'. Алгоритм: Функция negdist вычисляет взвешенный вход для векторов x и y в системе MATLAB следующим образом: z = –sqrt(sum(x – y).^2). Сопутствующие функции: sim, dotprod, dist.
Синтаксис:
Описание: Функция взвешивания Z = mandist(W, P) вычисляет расстояние в виде суммарного zij = sum(abs(wi – pj')). (11.3) Функция Z = mandist(W, P) вычисляет матрицу взвешенных входов для матрицы входов P размера R´Q и матрицы весов W размера S´R. Результатом является матрица Z размера S´Q. Функция df = dist('deriv') возвращает пустую строку, поскольку производная не определена. Функция mandist может быть использована как функция для вычисления расстояний между нейронами в слое. Функция расстояния D = mandist(pos) вычисляет расстояние между нейронами для сетей с топологией. Входной аргумент pos – это матрица координат расположения нейронов в N-мерном пространстве размера N´S; выходной аргумент D – это матрица расстояний размера S´S. Пример: Вычислим вектор взвешенных входов Z, если заданы случайные матрица весов Wразмера 4´3 и вектор входа P размера 3´1: W = rand(4,3); P = rand(3,1); Z = mandist(W,P) Z = 0.8265 0.9830 1.0359 1.7712 Результатом является вектор размера 4´1, вычисленный в соответствии с соотношением (11.2). Рассмотрим сеть с топологией, для которой задана случайная матрица координат pos = rand(3,10); D = mandist(pos) D = Columns 1 through 7 0 0.8589 0.6427 1.2565 0.8813 0.5815 0.7340 0.8589 0 0.6227 0.9084 1.2433 1.4404 0.7770 0.6427 0.6227 0 0.8333 1.5239 1.1681 1.2451 1.2565 0.9084 0.8333 0 0.9730 1.0287 1.5443 0.8813 1.2433 1.5239 0.9730 0 0.7039 1.1153 0.5815 1.4404 1.1681 1.0287 0.7039 0 1.2512 0.7340 0.7770 1.2451 1.5443 1.1153 1.2512 0 0.8268 0.8910 0.9289 1.7622 1.7081 1.3523 1.1911 1.0852 0.9757 0.4425 1.0977 1.9665 1.6107 1.5981 0.7504 1.1124 1.3930 1.2194 0.7122 0.9397 0.4031 Columns 8 through 10 0.8268 1.0852 0.7504 0.8910 0.9757 1.1124 0.9289 0.4425 1.3930 1.7622 1.0977 1.2194 1.7081 1.9665 0.7122 1.3523 1.6107 0.9397 1.1911 1.5981 0.4031 0 0.8238 1.5772 0.8238 0 1.8356 1.5772 1.8356 0 Применение функции: Функция суммарного координатного смещения используется в сетях с топологией, например в картах Кохонена newsom. Чтобы применить эту функцию для других сетей с топологией, необходимо установить значение свойства net.layerWeight{i,j}.distanceFcn равным 'mandist'. Чтобы применить функцию взвешивания mandist, следует установить свойство net.inputWeight{i, j}.weightFcn равным 'mandist'. Алгоритм: Сумммарное координатное смещение d между векторами x и y вычисляется в системе MATLAB следующим образом: d = sum(abs(x–y)). Сопутствующие функции: sim, dist, linkdist.
Синтаксис: d = boxdist(pos) Описание: Функция d = boxdist(pos) вычисляет расстояния максимального координатного смещения между нейронами слоя, если задан массив координат нейронов pos размера N´S, где N – размерность пространства расположения нейронов. Выходом является массив расстояний размера S´S. Функция boxdist обычно используется в сетях с функцией топологии gridtop. Пример: Пусть задан массив случайных координат трехмерного пространства, в которых размещены 10 нейронов. Требуется вычислить массив максимальных координатных смещений между этими нейронами. pos = rand(3,10); d = boxdist(pos) d = 0 0.1614 0.6100 0.5123 0.4512 0.3767 0.1614 0 0.5282 0.3509 0.2898 0.2714 0.6100 0.5282 0 0.4374 0.4965 0.3608 0.5123 0.3509 0.4374 0 0.3044 0.1805 0.4512 0.2898 0.4965 0.3044 0 0.1358 0.3767 0.2714 0.3608 0.1805 0.1358 0 0.2785 0.1967 0.4536 0.4855 0.4244 0.3499 0.4603 0.3119 0.6149 0.5709 0.5097 0.4353 0.5502 0.4720 0.6900 0.3611 0.6655 0.5298 0.2442 0.3926 0.5860 0.4280 0.5862 0.4504
0.2785 0.4603 0.5502 0.2442 0.1967 0.3119 0.4720 0.3926 0.4536 0.6149 0.6900 0.5860 0.4855 0.5709 0.3611 0.4280 0.4244 0.5097 0.6655 0.5862 0.3499 0.4353 0.5298 0.4504 0 0.2623 0.5234 0.4422 0.2623 0 0.7839 0.7045 0.5234 0.7839 0 0.4659 0.4422 0.7045 0.4659 0 Применение функции: Функция максимального координатного смещения используется в сетях с топологией, например в картах Кохонена newsom. Чтобы применить эту функцию для других сетей с топологией, необходимо установить значение свойства net.layerWeight{i,j}.distanceFcn равным 'boxdist'. Алгоритм: Максимальное координатное смещение d между векторами x и y вычисляется в системе MATLAB следующим образом: d = max(abs(x–y)). Сопутствующие функции: SIM, DIST, MANDIST, LINKDIST.
Синтаксис: d = linkdist(pos) Описание: Функция d = linkdist(pos) вычисляет расстояния связи между нейронами слоя, если задан массив координат нейронов pos размера N´S, где N – размерность пространства расположения нейронов. Выходом является массив расстояний размера S´S. Пример: Пусть задан массив случайных координат трехмерного пространства, в которых размещены 10 нейронов. Требуется вычислить массив расстояний связи между этими нейронами (рис. 11.41): pos = rand(3,10);
d=linkdist(pos) d = 0 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 0 2 1 2 1 1 1 1 1 1 2 0 1 1 1 2 2 1 1 1 1 1 0 1 1 1 1 1 1 1 2 1 1 0 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 2 1 1 1 0 1 1 1 1 1 2 1 1 1 1 0 Применение функции: Функция расстояния связи linkdist используется для оценки топологии при формировании слоя Кохонена newc и карты Кохонена newsom. Чтобы применить функцию расстояния связи linkdist, следует установить значение свойства net.layers{i}.distanceFcn равным 'linkdist'. Алгоритм: Расстояние связи dij между двумя позициями векторов posi и posj из множества S векторов определяется соотношением
Сопутствующие функции: sim, dist, mandist. Функции накопления Функции, задающие правила формирования входа нейрона, называются функциями накопления. Как правило, это либо сумма взвешенных входов, либо их поэлементное произведение.
Блок Simulink:
Синтаксис:
Описание: Функция N = netprod(Z1, Z2, ...) вычисляет функцию накопления потенциала нейрона в виде суммы элементов взвешенных входов Zi размера S´Q, где S – число нейронов
где символ Функция df = netsum('deriv') возвращает имя М-функции, которая вычисляет производную суммы массивов взвешенных входов. Функция dN_dZi = dnetprod(Zi, N) вычисляет производную от суммы взвешенных входов N по одному из входов. Здесь N, Zi и dN_dZi – массивы одинакового размера S´Q. Пример: Вычислить функцию накопления потенциала для следующих взвешенных входов: Z1 = [ 1 2 4; 3 4 1]; Z2 = [–1 2 2; –5 –6 1]; N = netsum(Z1,Z2) N = 0 4 6 –2 –2 2 Вычислить функцию накопления с учетом вектора смещения b. Поскольку массивы Z1 и Z2 составлены из трех векторов, то с помощью функции concur должен быть создан массив из трех копий вектора смещения b для того, чтобы все размерности совпадали: b = [0; –1]; N = netsum(Z1,Z2,concur(b,size(Z1,2))) N = 0 4 6 –3 –3 1 Определим 2 весовые матрицы входа для слоя с тремя нейронами: Z1 = [0; 1; –1]; Z2 = [1; 0.5; 1.2]; Вычислить вход нейрона N с помощью функции netsum и затем найти производные по каждому из взвешенных входов: N = netsum(Z1,Z2) dN_dZ1 = dnetsum(Z1,N) dN_dZ2 = dnetsum(Z2,N) N = 0 4 6 –2 –2 2 dN_dZ1 = 1 1 1 1 1 1 dN_dZ2 = 1 1 1 1 1 1 Применение функции: Функция вычисления потенциала netsum применяется в архитектуре персептрона Чтобы применить функцию вычисления потенциала netsum, следует установить Алгоритм: Производная суммы по любому элементу этой суммы всегда является массивом Сопутствующие функции: sim, netprod, concur.
Блок Simulink:
Синтаксис:
Описание: Функция N = netprod(Z1, Z2, ...) вычисляет функцию накопления потенциала нейрона в виде поэлементного произведения массивов взвешенных входов Zi размера S´Q, где
где символ Функция df = netprod('deriv') возвращает имя М-функции, которая вычисляет производную от поэлементного произведения массивов. Функция dN_dZi = dnetprod(Zi, N) вычисляет производную от поэлементного произведения взвешенных входов N по одному из входов. Здесь N, Zi и dN_dZi – массивы одинакового размера S´Q. Пример: Вычислить функцию накопления для следующих взвешенных входов: Z1 = [ 1 2 4; 3 4 1]; Z2 = [–1 2 2; –5 –6 1]; N = netprod(Z1,Z2) N = –1 4 8 –15 –24 1 Вычислить функцию накопления с учетом вектора смещения b. Поскольку массивы Z1 и Z2 составлены из трех векторов, то с помощью функции concur должен быть создан массив из трех копий вектора смещения b для того, чтобы все размерности совпадали: b = [0; –1]; N = netprod(Z1,Z2,concur(b,size(Z1,2))) N = 0 0 0 15 24 –1 Определим 2 взвешенных входа для слоя с тремя нейронами: Z1 = [0; 1; –1]; Z2 = [1; 0.5; 1.2]; Вычислить вход нейрона N с помощью функции netprod и затем найти производные по каждому из взвешенных входов: N = netprod(Z1,Z2); N' dN_dZ1 = dnetprod(Z1,N); dN_dZ1' dN_dZ2 = dnetprod(Z2,N); dN_dZ2' ans = 0 0.5000 –1.2000 ans = NaN 0.5000 1.2000 ans = 0 1 –1 Применение функции: Функция поэлементного произведения netprod применяется в архитектуре обобщенных регрессионных и вероятностных сетей, формируемых с помощью М-функций newgrnn и newpnn. Чтобы применить функцию вычисления потенциала netprod, следует установить Алгоритм: Производная поэлементного произведения взвешенных входов по каждому из них равна поэлементному произведению остальных взвешенных входов, за исключением особого случая, когда взвешенный вход содержит нулевой элемент. Сопутствующие функции: SIM, NETSUM, CONCUR. Функции инициализации Функции инициализации выполняют подготовку нейронной сети к инициализации
Синтаксис: net = init(net) Описание: Функция net = init(net) выполняет инициализацию нейронной сети, используя Пример: Сформировать персептрон с одним нейроном, вход которого имеет 2 элемента со значениями в диапазонах [0 1] и [ –2 2]. net = newp([0 1; –2 2], 1); net.initFcn net.layers{1}.initFcn net.inputWeights{1}.initFcn net.biases{1}.initFcn ans = initlay ans = initwb ans = initzero ans = initzero В результате создания персептрона мы видим, что сеть допускает возможность задавать любые функции инициализации весов и смещений, поскольку в качестве функций готовности выбраны: для сети – функция initlay, для слоя – initwb. В качестве функций инициализации для весов и смещений персептрона используется функция initzero. Выведем значения установленных весов и смещений: net.IW{1,1} net.b{1} ans = 0 0 ans = 0 Обучим персептрон на следующих обучающих множествах P = [0 1 0 1; 0 0 1 1]: T = [0 0 0 1]; net = train(net,P,T); net.IW{1,1} net.b{1} ans = 1 2 ans = –3 Это приводит к установлению новых значений весов и смещений. Для того чтобы возвратиться к начальным значениям весов и смещений, характерных для данной сети, и предназначена функция init: net = init(net); net.IW{1,1} net.b{1} ans = 0 0 ans = 0 Веса и смещения возвращаются к нулевым значениям, что соответствует свойствам нейронной сети персептрона. Алгоритм: Функция init проверяет свойство net.initFcn, чтобы инициализировать нужным образом веса и смещения. Обычно свойство net.initFcn устанавливается равным 'initlay', что позволяет устанавливать функции инициализации для каждого слоя, используя свойство net.layers{i}.initFcn. В сетях с обратным распространением ошибки свойство net.layers{i}.initFcn устанавливается равным 'initnw', что соответствует алгоритму инициализации Nguyen – Widrow. Для других сетей значение свойства net.layers{i}.initFcn устанавливается равным 'initwb', что позволяет устанавливать произвольные функции инициализации для каждого слоя. Наиболее общий тип функции инициализации – это функция rands, которая генерирует случайные значения весов и смещений в диапазоне [–1 1]. Сопутствующие функции: SIM, ADAPT, TRAIN, INITLAY, INITNW, INITWB, RANDS.
Синтаксис: net = initlay(net) info = initlay(code) Описание: Функция net = initlay(net) устанавливает, что в сети net для инициализации ее слоев могут быть использованы собственные функции инициализации, определяемые свойством net.layers{i}.initFcn. Функция info = initlay(code) возвращает информацию о параметрах инициализации, соответствующую следующим значениям аргумента code: 'pnames' – имена параметров инициализации; 'pdefaults' – значения параметров инициализации по умолчанию. Initlay не имеет параметров инициализации. Применение функции: Функция инициализации initlay используется при создании сетей с помощью методов newp, newlin, newff, newcf, а также при формировании сетей с атрибутами, определяемыми пользователем. Для того чтобы подготовить сеть к заданию произвольных функций инициализации слоев, необходимо: · установить свойство сети net.initFcn равным 'initlay'. Это автоматически установит свойство net.initParam равным пустой матрице [ ], так как функция initlay не имеет параметров инициализации; · установить значения свойств net.layers{i}.initFcn, соответствующие выбранным функциям инициализации для слоя, например initwb или initnw. Для того чтобы фактически инициализировать сеть, т. е. присвоить значения матрицам весов и векторам смещений, необходимо применить функцию init. Алгоритм: Веса и смещения в каждом слое i сети net инициализируются функцией, заданной значением свойства net.layers{i}.initFcn. Сопутствующие функции: initwb, initnw, init.
Синтаксис: net = initwb(net,I) Описание: Функция net = initwb(net, I) устанавливает, что в сети net для инициализации слоя I будет Применение функции: Функция инициализации initwb используется при создании сетей с помощью методов newp, newlin, newff, а также при формировании сетей с атрибутами, определяемыми пользователем. Для того чтобы подготовить сеть к заданию произвольных функций инициализации слоев, необходимо: · установить свойство сети net.initFcn равным 'initlay'. Это автоматически установит свойство net.initParam равным пустой матрице [ ], так как функция initlay не имеет параметров инициализации; · установить значение свойства net.layers{i}.initFcn равным 'initwb'; · установить значения свойств net.inputWeights{i, j}.initFcn, net.layerWeights{i, j}.initFcn, net.biases{i}.initFcn, соответствующие выбранным функциям инициализации, например rands или midpoint. Для того чтобы фактически инициализировать сеть, т. е. присвоить значения матрицам весов и векторам смещений, необходимо применить функцию init. Сопутствующие функции: initnw, initlay, init.
Синтаксис: net = initnw(net,I) Описание: Функция net = initnw(net, I) инициализирует веса и смещения слоя I сети net, используя алгоритм инициализации Nguyen – Widrow. Применение функции: Функция инициализации initnw используется при создании сетей с помощью методов newff, newcf, а также при формировании сетей с атрибутами, определяемыми пользователем. Для того чтобы подготовить сеть к заданию функции инициализации initnw, необходимо: · установить свойство сети net.initFcn равным 'initlay'. Это автоматически установит свойство net.initParam равным пустой матрице [ ], так как функция initlay не имеет параметров инициализации; · установить значение свойства net.layers{i}.initFcn равным 'initnw'. Для того чтобы фактически инициализировать сеть, т. е. присвоить значения матрицам весов и векторам смещений, необходимо применить функцию init. Алгоритм: Метод Nguyen – Widrow генерирует значения начальных весов и смещений так, чтобы активные области слоя нейронов были бы распределены приблизительно равномерно Его преимуществами по сравнению с методом инициализации случайных весов · оптимальное количество используемых нейронов; · ускорение процедуры обучения, поскольку активные зоны нейронов соответствуют пространству входа. Ограничения метода инициализации Nguyen – Widrow связаны с тем, что его можно применять только к слоям, имеющим смещения, с функцией взвешивания dotprod и функцией накопления netsum. Если эти условия не выполняются, то следует использовать метод инициализации rands. Сопутствующие функции: initwb, initlay, init.
IСинтаксис: W = initzero(S,PR) b = initzero(S,[1 1]) Описание: Функция W = initzero(S, PR) присваивает матрице весов слоя нулевые значения Входные аргументы: S – число нейронов в слое; PR – матрица размера R´2, задающая диапазоны изменения элементов входного вектора. Выходной аргумент: W – нулевая матрица весов размера S´R. Функция b = initzero(S, [1 1]) присваивает вектору смещений слоя нулевые значения Входной аргумент: S– число нейронов в слое. Выходной аргумент: b – нулевой вектор смещений размера S´1. Пример: Присвоить нулевые значения матрице весов и вектору смещения для слоя с пятью нейронами и вектором входа, элементы которого принимают значения в диапазонах [0 1], [–2 2]. W = initzero(5, [0 1; –2 2]) b = initzero(5, [1 1])
Применение функции: Функция инициализации initzero используется при создании сетей с помощью методов newp, newlin, а также при формировании сетей с атрибутами, определяемыми пользователем. Для того чтобы подготовить сеть к заданию функции инициализации initzero, необходимо: · установить свойство сети net.initFcn равным 'initlay'. Это автоматически установит свойство net.initParam равным пустой матрице [ ], так как функция initlay не имеет параметров инициализации; · установить значение свойства net.layers{i}.initFcn равным 'initwb'; · установить значения свойств net.inputWeights{i, j}.initFcn, net.layerWeights{i, j}.initFcn, net.biases{i}.initFcn равными initzero. Для того чтобы фактически инициализировать сеть, т. е. присвоить нулевые значения матрицам весов и векторам смещений, необходимо применить функцию init. Сопутствующие функции: initwb, initlay, init.
Синтаксис: W = midpoint(S,PR) Описание: Функция W = midpoint (S, PR) присваивает элементам матрицы весов слоя средние значения элементов вектора входа и имеет следующие входные и выходные аргументы. Входные аргументы: S – число нейронов в слое; PR – матрица размера R´2, задающая диапазоны изменения элементов входного вектора [Pmin Pmax]. Выходной аргумент: W – матрица весов размера S´R с элементами столбцов, равными (Pmin+Pmax)/2. Пример: Присвоить нулевые значения матрице весов и вектору смещения для слоя с пятью нейронами и вектором входа, элементы которого принимают значения в диапазонах [0 1], [–2 2]. W = midpoint(5,[0 1; –2 2]) W = 5.0000e–001 0 5.0000e–001 0 5.0000e–001 0 5.0000e–001 0 5.0000e–001 0 Применение функции: Функция инициализации midpoint используется при создании сетей с помощью метода newp, а также при формировании сетей с атрибутами, определяемыми пользователем. Для того чтобы подготовить сеть к заданию функции инициализации midpoint, необходимо: · установить свойство сети net.initFcn равным 'initlay'. Это автоматически установит свойство net.initParam равным пустой матрице [ ], так как функция initlay не имеет параметров инициализации; · установить значение свойства net.layers{i}.initFcn равным 'initwb'; · установить значения свойств net.inputWeights{i, j}.initFcn, net.layerWeights{i, j}.initFcn равными midpoint. Для того чтобы фактически инициализировать сеть, т. е. присвоить нулевые значения матрицам весов и векторам смещений, необходимо применить функцию init. Сопутствующие функции: INITWB, INITLAY, INIT.
Синтаксис: W = rands(S,PR) M = rands(S,R) v = rands(S) Описание: Функции семейства rands предназначены для инициализации случайных массивов весов и смещений. Функция W = rands(S, PR) имеет 2 входных аргумента: S – число нейронов; PR– массив минимальных и максимальных значений вектора входа размера R´2. Выходом является случайная матрица весов размера S´R с элементами из диапазона [–1 1]. Функция M = rands(S, R) использует в качестве второго аргумента параметр R, соответствующий числу элементов вектора входа. Выходом также является случайная матрица весов размера S´R с элементами из диапазона [–1 1]. Функция v = rands(S) возвращает случайный вектор размера S´1 с элементами из диапазона [–1 1]. Пример: Сформируем с помощью функции rands различные массивы случайных величин: W = rands(4,[0 1; –2 2]) M = rands(2,3) v = rands(4) W = 0.9003 0.7826 –0.5377 0.5242 0.2137 –0.0871 –0.0280 –0.9630 M = 0.6428 0.2309 0.8436 –0.1106 0.5839 0.4764 v = –0.6475 –0.1886 0.8709 0.8338 Применение функции: Для того чтобы подготовить сеть к заданию функции инициализации rands, необходимо: · установить свойство сети net.initFcn равным 'initlay'. Это автоматически установит свойство net.initParam равным пустой матрице [ ], так как функция initlay не имеет параметров инициализации; · установить значение свойства net.layers{i}.initFcn равным 'initwb'; · установить значения свойств net.inputWeights{i, j}.initFcn, net.layerWeights{i, j}.initFcn равными rands. Для того чтобы фактически инициализировать сеть, т. е. присвоить случайные значения матрицам весов и векторам смещений, необходимо применить функцию init. Сопутствующие функции: RANDNR, RANDNC, INITWB, INITLAY, INIT.
Синтаксис: W = randnc(S,PR) W = randnc(S,R) Описание: Функции семейства randnc аналогичны функциям rands, но предназначены только для инициализации весов. К ним возможны 2 формы обращения, которые возвращают случайную матрицу весов размера S´R с нормированными столбцами. Пример: Сформируем случайный массив из четырех нормированных трехэлементных столбцов: M = randnc(3,4) M = –0.6007 –0.4715 –0.2724 0.5596 –0.7628 –0.6967 –0.9172 0.7819 –0.2395 0.5406 –0.2907 0.2747 Сопутствующие функции: randnr, randS.
Синтаксис: W = randnr(S,PR) W = randnr(S,R) Описание: Функции семейства randnr аналогичны функциям rands, но предназначены только Пример: Создадим случайную матрицу из трех нормированных четырехэлементных строк: W = randnr(3,4) W = 0.9713 0.0800 –0.1838 –0.1282 0.8228 0.0338 0.1797 0.5381 –0.3042 –0.5725 0.5436 0.5331 Сопутствующие функции: randnC, randS.
Синтаксис: b = initcon(S,PR) Описание: Функция initcon является функцией инициализации смещений, которая инициализирует смещения для сети с функцией настройки learncon. Функция b = initcon(S, PR) присваивает значения вектору смещения и имеет следующие входные и выходные аргументы. Входные аргументы: S – число нейронов в слое; PR – матрица размера R´2, задающая диапазоны изменения элементов входного Выходной аргумент: b – вектор смещений размера S´1. Функция initcon может также быть использована для инициализации весов, но применение ее для этой цели не рекомендуется. Пример: Начальные значения смещений рассчитаем для слоя с пятью нейронами: b = initcon(5) b’ = 1.3591e+001 1.3591e+001 1.3591e+001 1.3591e+001 1.3591e+001 Применение функции: Функция инициализации initcon используется при создании сетей с помощью метода newc, а также при формировании сетей с атрибутами, определяемыми пользователем. Для того чтобы подготовить сеть к заданию функции инициализации midpoint, · установить свойство сети net.initFcn равным 'initlay'. Это автоматически установит свойство net.initParam равным пустой матрице [ ], так как функция initlay не имеет параметров инициализации; · установить значение свойства net.layers{i}.initFcn равным 'initwb'; · установить свойство net.biases{i}.initFcn на 'initcon'. Для того чтобы фактически инициализировать сеть, необходимо применить функцию init. Алгоритм: Функция learncon модифицирует смещения так, чтобы значение каждого смещения b(i) являлось функцией среднего значения выхода для нейрона с номером i. Начальные значения смещений устанавливаются равными b(i) = exp(1)´S. Сопутствующие функции: INITWB, INITLAY, INIT, LEARNCON.
Синтаксис: net = revert(net) Описание: Функция net = revert(net) возвращает веса и смещения к значениям, соответствующим последней процедуре инициализации. Если же изменениям подвергались связи между нейронами или изменялось их количество, то функция revert не может восстановить прежних значений и присваивает весам и смещениям нулевые значения. Сопутствующие функции: INIT, SIM, ADAPT, TRAIN. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Рис. 11.41
Рис. 11.41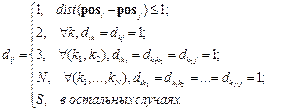
 , (11.4)
, (11.4)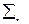 обозначает поэлементное сложение.
обозначает поэлементное сложение.
 , (11.5)
, (11.5) обозначает поэлементное произведение.
обозначает поэлементное произведение.