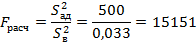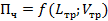|
|
АНАЛИЗ СТАТИСТИЧЕСКИХ СВОЙСТВ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ ШЕРОХОВАТОСТИ ПОВЕРХНОСТИ ПИЛОМАТЕРИАЛОВ12
Исходные данные для определения процента годной продукции и требуемой точности настройки раскряжевочной установки. Таблица 4.1
Заданные в виде простого статистического ряда длины сортиментов распологаем в виде неубывающей последовательности, т.е. строим вариационный ряд.
Таблица 4.2
С помощью t-критерия Стьюдента исключаем из вариационного ряда анормальные результаты наблюдений. Для этого вычисляем: Выборочное среднее:
Выборочную дисперсию:
Выборочное среднеквадратическое отклонение:
Расчетный t-критерий:
По числу степеней свободы Если
Продолжаем проверку выборки №1.
Таблица 4.3
Выборочное среднее:
Выборочную дисперсию:
Выборочное среднеквадратическое отклонение:
Расчетный t-критерий:
По числу степеней свободы
Проверяем однородность дисперсии по F-критерию Филера.
Задаем уровень значимости: Число степеней свободы: По значениею f1 и f2 определяем табличное значение критерия Фишера: Получаем
Проверяем однородность выборочных средних. S1 и S2 неоднородны, в данном случае формула tрасч имеет вид:
Найденое значение f округляем до целого и принимаем за число степеней свободы. По этой величине и по уровню значимости
Проверяем оценку точности и надежности математического ожидания:
Определяе потребный объем случайной выборки: Если задаться допустимой производственнной точностью шероховатости поверхности пиломатериалов ∆и доверительной вероятностью
Вывод: анализ статистических свойств измерений шероховатостей поверхности материалов показал, что необходимое число замеров
ОПРЕДЕЛЕНИЕ ЗАВИСИМОСТИ ШЕРОХОВАТОСТИ ВЫПИЛИВАЕМЫХ ДОСОК ОТ ВРЕМЕНИ РАБОТЫ РАМНЫХ ПИЛ ПОСЛЕ ЗАТОЧКИ
Исходные данные: x — время работы рамных пил после заточки, ч y — шероховатость поверхности досок, мм
Таблица 5.1
Определяем коэффициент корреляции r между временем работы пил после заточки и шерохроватости поверхности выпиливаемых досок h.
Коэффициент корреляции r вычисляем по формуле:
Оценка значимости коэффициента корреляции производится с помощью t-критерия. Для этого определяется:
Оцениваем коэффициенты регрессии линейной и квадратичной моделей. Регрессионная модель в виде линейного уравнения имеет вид:
Коэффициенты регрессии определяем, решив систему уравнений:
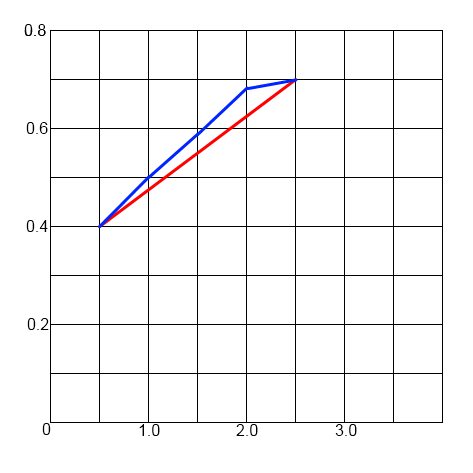
Строим график:
Рис. 5.1
Регрессионная модель в виде квадратичного уравнения имеет вид: Для нахождения трех неизвестных коэффициентов регрессии, решим систему из трех линейных уравнений с тремя неизвестными:
Подставляем все значения в последнее уравнение:
Строим график зависимости:
Рис. 5.2 График зависимости шероховатости досок от времени работы рамных пил
Вывод: в соответствии с проведенным анализом, мы выяснили, что зависимость шероховатости выпиливаемых досок от времени работы рамных пил после заточки определяется по линейной зависимости.
ОБРАБОТКА РЕЗУЛЬТАТОВ ПОЛНОФАКТОРНОГО ПЛАНА И ПОСТРОЕНИЕ РЕГРЕССИОННОЙ ЗАВИСИМОСТИ ПРОИЗВОДИТЕЛЬНОСТИ ТРЕЛЕВОЧНЫХ МАШИН
Исходные данные: Lтр — среднее расстояние трелевки, м; Vхл — средний объем хлыста, м3; Пч — часова производительность, м3/ч
Таблица 6.1
Результаты расчета и эксперимента сводим в таблицу.
Таблица 6.2
Определим уровни и интервалы варьирования факторов:
Аналогично находим верхний и нижний уровни варьирования среднего объема хлыста.
Рассчитываем средние и дисперсии для каждой серии опытов по формулам:
Отбрасываем аномальные результаты эксперимента и рассчитываем дисперсию воспромизводимости для каждой серии опытов. Находим интервал мат. ожидания для каждой выборки:
Результаты эксперимента не входящие в полученные диапазоны из табл.6.2 удаляем и пересчитываем значения
Таблица 6.3
Проверяем нормальность результатов:
Для проверки однородности нескольких дисперсий при равных объемах выборок
По выбранному уровню значимости q, числу степеней свободы каждой выборки Вычисляем дисперсию воспроизводимости по формуле:
Число степеней свободы f для данной дисперсии равно:
Рассчитываем коэффициенты регрессионной модели вида
Регрессионная модель в натуральных обозначениях будет иметь вид:
Запишем регрессионную модель в натуральных обозначениях:
Оцениваем степень значимости коэффициентов регрессии:
Вычисленную величину
Проверка адекватности математической модели даст возможность ответить на вопрос, будет ли построенная модель предсказывать значения выходной величины с той же точностью, что и результаты эксперимента. Определяем сумму квадратов, характеризующую адекватность модели:
Вычисляем число степеней свободы дисперсии адекватности:
Вычисляем дисперсию адекватности:
C помощью F-критерия Фишера проверяем однородность дисперсии адекватности
Модель неадекватна.
Строим графики зависимости
Рис. 6.1 График зависимости в нормальных обозначениях
Рис. 6.2 График зависимости в натуральных обозначениях

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
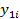




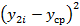
 ;
; ;
; ;
; ;
; ;
; ;
; ;
;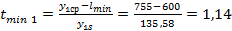 ;
;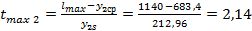 ;
; .
. , принятому уровню значимости
, принятому уровню значимости  определяем t-критерий Стьюдента.
определяем t-критерий Стьюдента. 
 и
и  , то гипотеза отвергается, значения
, то гипотеза отвергается, значения  и
и 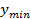 признаются анормальными и исключаются из выборки. Проверку такого рода необходимо производить до тех пор, пока не выполнится условие:
признаются анормальными и исключаются из выборки. Проверку такого рода необходимо производить до тех пор, пока не выполнится условие:  и
и  .
. — условие не выполняется.
— условие не выполняется. — условие выполняется.
— условие выполняется.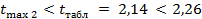 — условие выполняется.
— условие выполняется. — условие выполняется.
— условие выполняется. ;
;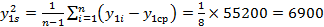 ;
; ;
; ;
; .
. , принятому уровню значимости
, принятому уровню значимости 
 — условие выполняется.
— условие выполняется. — условие выполняется.
— условие выполняется.

 ;
; 

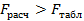 , значит выборочные дисперсии считаются неоднородными для выбранного уровня значимости q.
, значит выборочные дисперсии считаются неоднородными для выбранного уровня значимости q.










 , то можно определить потребный объем выборки.
, то можно определить потребный объем выборки.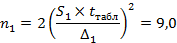

 и
и 





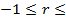



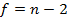 ,
, 
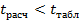 , значит принимает гипотезу о некоррелированности величин x и y. В противном случае r значимо отличается от 0, т.е. между величинами x и y существует линейная статическая связь.
, значит принимает гипотезу о некоррелированности величин x и y. В противном случае r значимо отличается от 0, т.е. между величинами x и y существует линейная статическая связь.


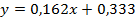
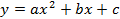
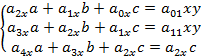

















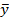
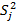

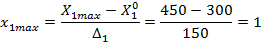

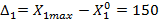
 — основной уровень варьирования фактора;
— основной уровень варьирования фактора;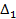 — интервал варьирования фактора.
— интервал варьирования фактора.






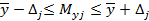

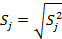











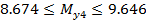
 и
и 







 может быть использован G-критерий Кохрена. Пусть
может быть использован G-критерий Кохрена. Пусть  . Вычислим расчетное G-отношение по формуле:
. Вычислим расчетное G-отношение по формуле:
 и по количеству выборок N из таблицы распределения Кохрена выбираем величину
и по количеству выборок N из таблицы распределения Кохрена выбираем величину  .
.  , следовательно гипотеза о однородности дисперсий неверна.
, следовательно гипотеза о однородности дисперсий неверна.

 для нормальных и натуральных факторов. Находим функции отклика.
для нормальных и натуральных факторов. Находим функции отклика.






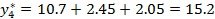
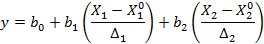

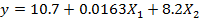



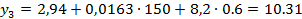
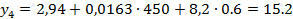





 сравниваем с табличным значением
сравниваем с табличным значением  критерия Стьюдента для заданного уровня значимости
критерия Стьюдента для заданного уровня значимости  и числа степеней свободы
и числа степеней свободы  .
.



 и дисперсии воспроизводимости
и дисперсии воспроизводимости  :
: