
|
|
СИМПЛЕКС-МЕТОД ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ12 (Идея симплекс-метода) Чтобы решить задачу ЛП надо представить ее в каноническом виде:
С помощью метода Жордана-Гаусса преобразуем систему (2) и выделим базисные переменные. Если Если Получаем преобразованную задачу:
В этой задаче: 1. Система ограничений выражена через свободные переменные; 2. Целевая функция выражена через свободные переменные; 3. Все 4. Все Это условие может быть обеспечено только в том случае, если система ограничений (4.2) имеет хотя бы одно неотрицательное решение. Одно из решений системы (4.4) получается, если в ней свободные неизвестные приравнять к 0. Получаем базисное решение:
Симплекс-метод состоит в переходе от одного базисного решения к другому базисному решению, такому, что целевая функция F будет увеличиваться. При этом рассматриваются коэффициенты целевой функции. Рассмотрим коэффициенты при свободных неизвестных в целевой функции:
Возможны следующие случаи: Случай 1. Среди коэффициентов целевой функции (3) нет положительных:
Тогда если увеличивать любую свободную переменную, то целевая функция (4.3) будет уменьшаться. Т.к. ищем максимальное решение, то уже найденное решение и будет оптимальным. Но оно может быть не единственным, если в целевой функции (4.3) есть коэффициенты, равные 0. Случай 2. Среди коэффициентов целевой функции (4.3) найдется хотя бы один положительный, например Положим в уравнениях (4.3) и (4.4) все свободные переменные равными нулю, кроме Тогда система (4.4) и уравнение (4.3) примут вид:
Если Возможны следующие случаи: Случай 1. Предположим, что среди коэффициентов нет положительных, т.е., Случай 2. Предположим, что среди коэффициентов есть положительные, тогда требование неотрицательности переменных приводит к неравенствам вида:
Это означает, что: Максимальное значение, которое может принимать переменная Допустим, что оно достигается при
Элемент
Далее целевую функцию (4.3) и систему (4.4) записываем через новые свободные переменные.
И снова рассматривается новая целевая функция, если какую-нибудь переменную можно увеличить, то весь процесс повторяется. Если все коэффициенты при переменных (в целевой функции) не положительны, то найдено оптимальное решение. Этапы решения задачи ЛП симплекс-методом: 1. Записываем систему ограничений в каноническом виде; 2. Записываем базисное решение; 3. Выбираем переменную из целевой функции, которую будем увеличивать; 4. Определяем возможность роста переменной из системы ограничений; 5. Среди уравнений выбираем то, где рост переменной минимален; 6. Делаем выбранную переменную базисной, а базисную свободной; 7. Записываем систему ограничений и целевую функцию через новую свободную переменную; 8. И далее все повторяется со второго пункта, пока можно выбирать переменную из целевой функции. Пример 4.1. Озеро можно заселить двумя видами рыб А и В. Средняя масса рыбы для вида А равна 2 кг и для вида В – 1 кг. В озере имеется два вида пищи: P1 и Р2. Средние потребности одной рыбы вида А составляют 1 ед. корма P1 и 3 ед. корма P2 в день. Аналогичные потребности для рыбы вида В составляют 2 ед. P1 и 1 ед. P2. Ежедневный запас пищи поддерживается на уровне500 ед. P1 и 900 ед. Р2. Как следует заселить озеро рыбами, чтобы максимизировать общую массу рыб? Решение. Для удобства оформим данные задачи в таблице.
Составим математическую модель задачи. Введем переменные задачи: х1 – количество рыб вида А; x2 – количество рыб вида В. Составим систему ограничений: Зададим целевую функцию. Масса рыб 1.Запишем эту задачу в виде основной ЗЛП, для этого перейдем от системы неравенств к равенствам (канонический вид), для этого введем две дополнительные переменные:
2. Запишем базисное решение. F0(0;0;500;900) = 0. 3. Выбираем переменную 4. Определяем возможность роста переменной из системы ограничений.
5. Выбираем второе уравнение, т.к. рост переменной минимален. 6. Делаем выбранную переменную базисной, а базисную свободной.
7. Записываем систему ограничений и целевую функцию через новую свободную переменную. Подставим
8.
Далее все повторяется со второго пункта, пока можно выбирать переменную из целевой функции. 2. Запишем базисное решение. F1 (300;0;200;0) = 0. 3. Выбираем переменную 4. Определяем возможность роста переменной из системы ограничений.
5. Выбираем первое уравнение, т.к. рост переменной минимален. 6. Делаем выбранную переменную базисной, а базисную свободной.
7. Записываем систему ограничений и целевую функцию через новую свободную переменную. Подставим
8.
Далее все повторяется со второго пункта, пока можно выбирать переменную из целевой функции. 2. Запишем базисное решение. F1 (260;120;0;0) = 640. 3. Выбираем переменную из целевой функции Ответ: Для получения максимального веса рыб 640кг, следует заселить 260 рыб вида А и 120 рыб вида В.
Пример 4.2. Для изготовления различных изделий А, В и С предприятие использует три различных вида сырья. Нормы расхода сырья на производство одного изделия каждого вида, цена одного изделия А, В и С, а также общее количество сырья каждого вида, которое может быть использовано предприятием, приведены в таблице. Составить план производства изделий, при котором общая стоимость всей произведенной продукции будет максимальной.
Решение: Составим математическую модель. Обозначим:
Запишем систему ограничений:
Общая стоимость произведенных товаров составляет: По экономическому содержанию переменные 1.Запишем эту задачу в виде основной ЗЛП, для этого перейдем от системы неравенств к равенствам (канонический вид), для этого введем три дополнительные переменные:
2. Запишем базисное решение. F0(0;0;0;120;96;180) = 0. 3. Выбираем переменную 4. Определяем возможность роста переменной из системы ограничений.
5. Выбираем второе уравнение, т.к. рост переменной минимален. 6. Делаем выбранную переменную базисной, а базисную свободной.
7. Записываем систему ограничений и целевую функцию через новую свободную переменную. Подставим
8.
Далее все повторяется со второго пункта, пока можно выбирать переменную из целевой функции. 2. Запишем базисное решение. F1(0;0;24;24;0;108) = 384. 3. Выбираем переменную 4. Определяем возможность роста переменной из системы ограничений.
5. Выбираем первое уравнение, т.к. рост переменной минимален. 6. Делаем выбранную переменную базисной, а базисную свободной.
7. Записываем систему ограничений и целевую функцию через новую свободную переменную. Подставим
8.
Далее все повторяется со второго пункта, пока можно выбирать переменную из целевой функции. 2. Запишем базисное решение. F2(0;8;20;0;0;96) = 400. 3. Выбираем переменную из целевой функции Ответ: Для получения максимальной стоимости всей произведенной продукции 400?, необходимо производить 0 изделий вида А, 8 изделий вида В и 20 изделие вида С.
Рассмотрим решение задач симплексным методом используя построение симплексных таблиц. Пример 5.1. На приобретение мебели для офиса предприятием было выделено средств на сумму 70 тыс. руб. Мебель должна быть размещена на общей площади, не превышающей 100 м². Предприятие может заказать мебель двух типов: А и В, стоимостью 15 тыс. руб. и 10 тыс. руб. соответственно. Мебели типа А требуется 12 м² площади (с учетом проходов), мебели типа В – 14 м² (с учетом проходов). Доход от эксплуатации мебели типа А составляет 18 тыс. руб. в месяц, В – 12 тыс. руб. в месяц. Найти оптимальный вариант приобретения мебели, обеспечивающей максимум прибыли для данного предприятия. Решение: Составим математическую модель задачи. Введем переменные задачи: х1 – количество мебели вида А, x2 – количество мебели вида В. Составим систему ограничений:
Зададим целевую функцию: F(x) = 18x1 + 12x2 → max Решение. Запишем данную задачу в форме основной задачи линейного программирования. Для этого перейдем от ограничений-неравенств к ограничениям-равенствам. Введем две дополнительные переменные, в результате чего ограничения запишутся в виде системы уравнений
где, x3 - остаток выделенных средств (тыс. руб.) на приобретение мебели, x4 - остаток площади (м²) на которой размещается мебель. F(x) = 18∙x1 + 12∙x2 + 0∙x3 + 0∙x4→ max - данная задача представлена в каноническом виде; - система уравнений приведена к единичному базису; - каждое уравнение системы ограничений содержит базисную переменную; - правые части всех ограничений неотрицательны. Строим симплекс – таблицу, имеющую следующий вид:
где Б.П. – столбец базисных переменных С – содержит коэффициенты при базисных переменных в целевой функции; b – столбец свободных членов; ∆к – индексная строка. По ее данным определяется, является ли решение оптимальным. Заполним таблицу по данным задачи. Вводим коэффициенты из системы ограничений и заполняем индексную строку коэффициентами целевой функции, взятыми с противоположными знаками. В столбец Б.П. записываем базисные (новые введенные) переменные x3 , x4 . В столбце С и над переменными записываем коэффициенты переменных целевой функции.
Проверим данный план на оптимальность. Если целевая функция исследуется как максимум, то в оптимальном плане все оценки должны быть ≥ 0. Если индексная строка не отвечает критериям оптимальности, то план можно улучшить. У нас все оценки отрицательны. Используем метод Жордана – Гаусса. Сначала выбирается разрешающий столбец и разрешающаяся строка, на их пересечении – разрешающий элемент. Для выбора разрешающегося столбца необходимо среди всех отрицательных оценок индексной строки выбрать наименьшее отрицательное число. В нашем случае это -18. Если окажется, что наименьших равных между собой элементов индексной строки имеется несколько, то рекомендуется выбрать первый (левый) элемент. Если в разрешающем столбце в некоторой таблице все коэффициенты не положительны, то целевая функция неограничена на множестве допустимых планов и задачу рушить нельзя. Разрешающий столбец показывает, какая переменная на следующем этапе перейдет из свободных в базисные. Для выбора разрешающей строки в столбцах Ө составляем следующие отношения Разрешающие столбец и строку обозначим стрелками. В нашем случае вместо переменной x3 в базисе будет переменная x1. На пересечении разрешающего столбца и строки получаем разрешающий элемент.
После выбора разрешающего элемента, строится новая симплексная таблица следующим образом: из базиса выводится переменная разрешающей строки, а в базис вводится переменная разрешающего столбца и заполняется вновь столбец С. Разделив все элементы разрешающей строки предыдущей таблицы на разрешающий элемент, результаты деления вносят в строку следующей таблицы, соответствующую введенной в базис переменной. На месте разрешающего элемента в следующей таблице будет стоять единица, а в остальных клетках разрешающего столбца, включая клетку индексной строки, стоят нули.
Oстальные элементы рассчитываются по методу Жордана –Гаусса. Чтобы заполнить вторую строку, соответствующую базисной переменной x4, необходимо все элементы преобразованной строки умножить на коэффициент, стоящий на пересечении второй строки и разрешающего столбца предыдущей таблицы и вычесть из соответствующих элементов второй строки этой же таблицы, а результат записать во вторую строку новой таблицы и т.д.
Полученный план проверяем на оптимальность. Получаем, F = 84. Опорное решение Х = (
Рассчитываем по методу Жордана –Гаусса последнюю симплекс таблицу.
Получаем: F = 84; Х = (0; 7; 0; 2). Ответ: Для того чтобы обеспечить максимальную прибыль 84 тыс. руб., предприятию можно приобрести только 7 шт. мебели вида В. Рассмотрим решение примеров 4.1. и 4.2. с помощью симплексных таблиц. Пример 5.2. (решение примера 4.1.)
Перейдя от системы неравенств к равенствам, получаем:
Решение. Таблица 1
Таблица 2
Таблица 3
Ответ: F(x) = 640, X = (260, 120, 0, 0), т.е. для получения максимального веса рыб 640 кг, следует заселить 260 рыб вида А и 120 рыб вида В.
Пример 5.3. (решение примера 4.2.)
Перейдя от системы неравенств к равенствам, получаем:
Решение. Таблица 1
Таблица 2
Таблица 3
Ответ: Для получения максимальной стоимости всей произведенной продукции 400?, необходимо производить 0 изделий вида А, 8 изделий вида В и 20 изделие вида С. ТРАНСПОРТНАЯ ЗАДАЧА Математическая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из т пунктов отправления А1, А2, …, Ат в п пунктов назначения В1, В2, …, Вп. При этом в качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки. Рассмотрим транспортную задачу, в качестве критерия оптимальности которой взята минимальная стоимость перевозок всего груза. Обозначим: cij – тарифы перевозки единицы груза из i-го пункта отправления в j-й пункт назначения, ai – запасы груза в i-м пункте отправления, bj – потребности в грузе в j–м пункте назначения, xij – количество единиц груза, перевозимого из i-го пункта отправления в j-й пункт назначения. Тогда математическая постановка задачи состоит в определении минимального значения функции: при условиях
Всякое неотрицательное решение систем линейных уравнений (6.2) и (6.3), определяемое матрицей Х=(хij), называется планом транспортной задачи. План Х*=(х*ij), при котором функция (6.1) принимает свое минимальное значение, называется оптимальным планом транспортной задачи. Обычно исходные данные транспортной задачи записывают в виде таблицы. Для определения опорного плана существует несколько методов: метод северо-западного угла, метод наименьшей стоимости, метод аппроксимации Фогеля и др. Метод северо-западного угла В самую северо-западную клетку таблицы заносится максимально допустимая перевозка, при этом либо вывозится весь груз со станции А1 и все остальные клетки первой строки вычеркиваются, либо потребности первого потребителя В1 полностью удовлетворяются, тогда все клетки первого столбца вычеркиваются. После этого самой северо-западной клеткой становится клетка А1В2 или В2А1. Алгоритм продолжается до заполнения таблицы. Недостатки – не учитывается стоимость перевозки, и получается план далекий от оптимального. Метод наименьшей стоимости Метод в какой-то степени учитывает затраты на перевозки и строится следующим образом: рассматривается матрица и находится клетка с наименьшей стоимостью, которая заполняется максимально допустимой перевозкой. В большинстве случаев этот метод дает план близкий к оптимальному. Метод аппроксимации Фогеля На каждой итерации по всем столбцам и по всем строкам находят разность между двумя записанными в них минимальными тарифами. Эти разности записываются в специально отведенных для этого строке и столбце таблице условий задачи. Среди указанных разностей выбирают минимальную. В строке или столбце, которой данная разность соответствует, определяют минимальный тариф. Широко распространенным методом решения транспортных задач является метод потенциалов. Данный метод позволяет оценить начальное опорное решение и методом последовательного улучшения найти оптимальное решение. Теорема 1. Если опорный план Х=(хij) является оптимальным, существует система из (т+п) чисел, называемых потенциалами, Ui, Vj, такая, что: • Ui+ Vj=Сij ,для хij>0 (базисные переменные); • Ui+ Vj=Сij ,для хij=0 (свободные переменные). 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
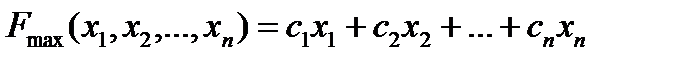 (4.1)
(4.1) (4.2)
(4.2) , то система имеет единственное решение, подставляем его в целевую функцию (1) и получаем решение задачи ЛП.
, то система имеет единственное решение, подставляем его в целевую функцию (1) и получаем решение задачи ЛП.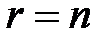 , то выражаем базисные переменные через свободные. Пусть базисные переменные –
, то выражаем базисные переменные через свободные. Пусть базисные переменные – 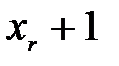 ,…,
,…,  ,свободные переменные –
,свободные переменные –  .
. (4.3)
(4.3) (4.4)
(4.4) ;
; .
.
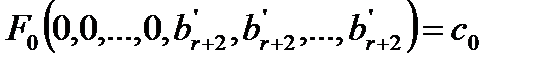
 (4.3)
(4.3)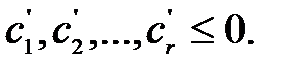
 .
.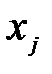 .
. (4.5)
(4.5) (4.6)
(4.6)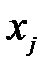 увеличивать, то будет увеличиваться и целевая функция (4.5), но возможность роста определяется системой (4.6) и зависит от знаков коэффициентов
увеличивать, то будет увеличиваться и целевая функция (4.5), но возможность роста определяется системой (4.6) и зависит от знаков коэффициентов  .
. ,тогда любая переменная
,тогда любая переменная  ,
,  либо не изменяется (если
либо не изменяется (если  ), либо растет (если
), либо растет (если 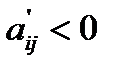 ), с ростом
), с ростом  .
. , для тех индексов
, для тех индексов  , у которых
, у которых  .
.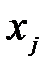 , равно минимальному из отношений
, равно минимальному из отношений  .
. , т.е.:
, т.е.: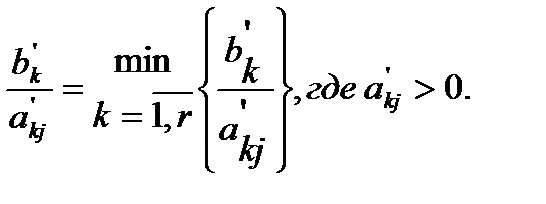
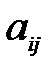 называется разрешающим элементом.
называется разрешающим элементом.  уходит в разряд базисных переменных, а
уходит в разряд базисных переменных, а  становится свободной переменной.
становится свободной переменной.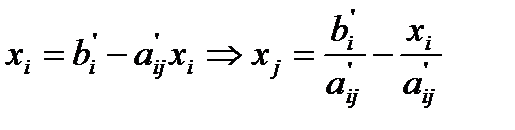
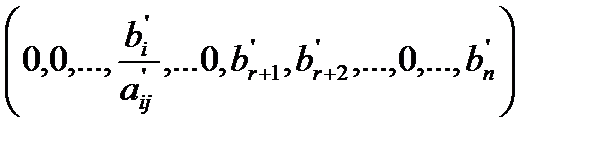
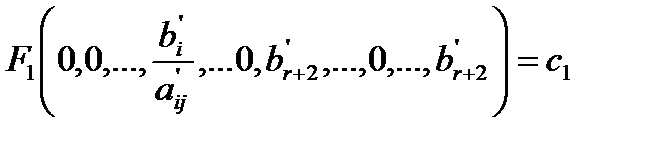
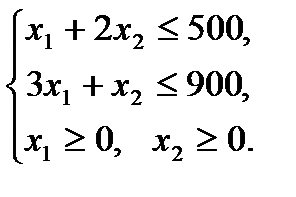
 → max.
→ max.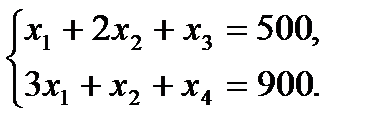

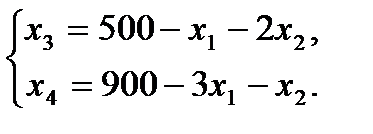
 из целевой функции
из целевой функции  , которую будем увеличивать.
, которую будем увеличивать.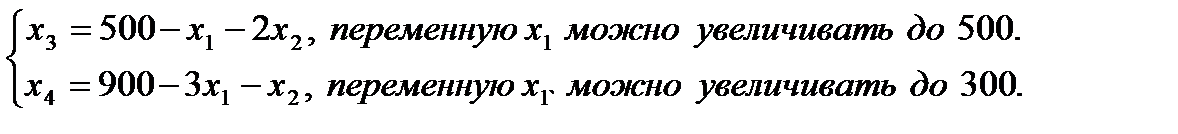
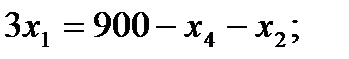
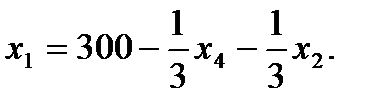
 и целевую функцию.
и целевую функцию.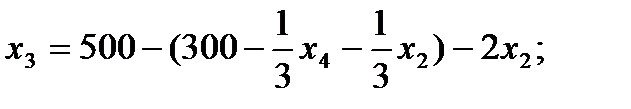
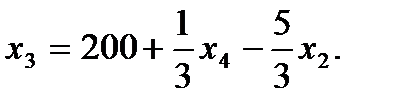
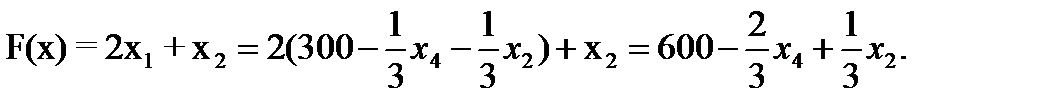

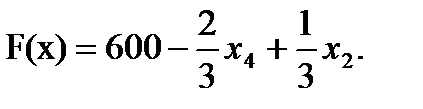
 из целевой функции
из целевой функции 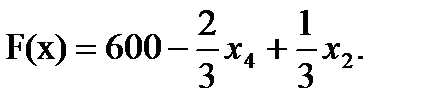 , которую будем увеличивать.
, которую будем увеличивать.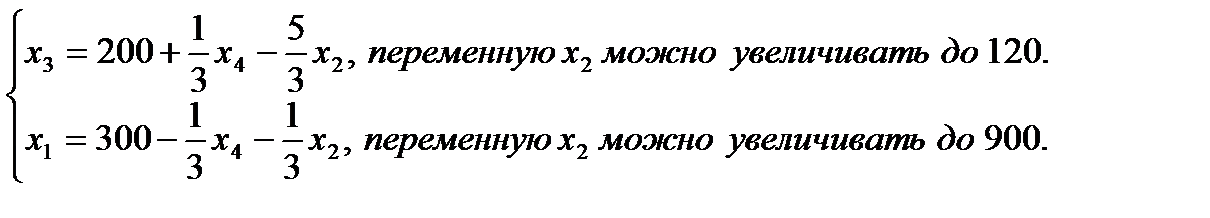
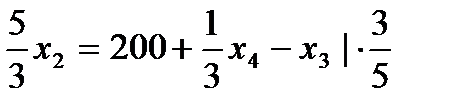
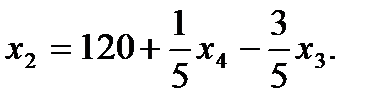
 и целевую функцию.
и целевую функцию.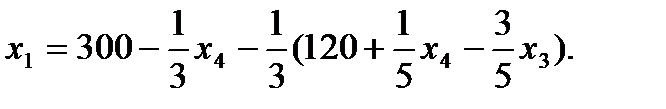
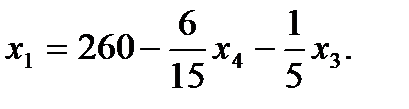
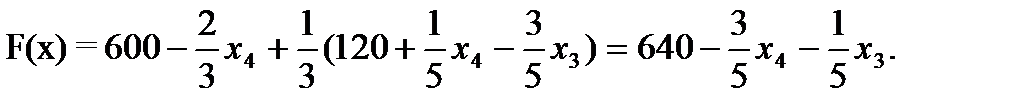
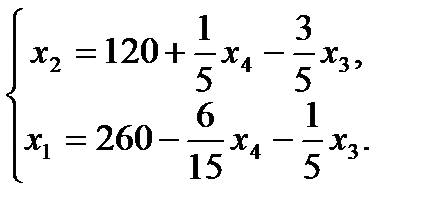
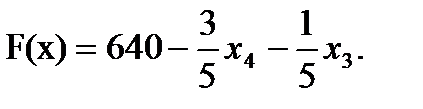
 , которую будем увеличивать. Видим, что увеличивая любую свободную переменную, целевая функция будет уменьшаться. Значит уже найденное решение и будет оптимальным.
, которую будем увеличивать. Видим, что увеличивая любую свободную переменную, целевая функция будет уменьшаться. Значит уже найденное решение и будет оптимальным.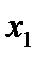 – выпуск изделий вида А;
– выпуск изделий вида А; – выпуск изделий вида С.
– выпуск изделий вида С.
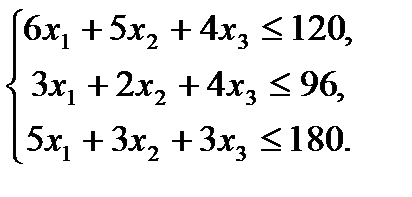
 .
.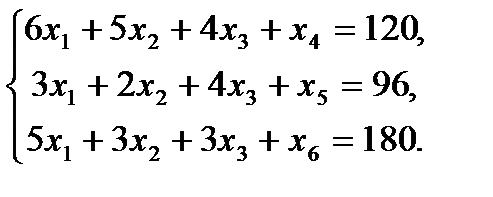
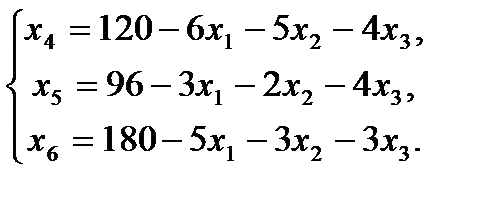
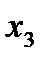 из целевой функции
из целевой функции 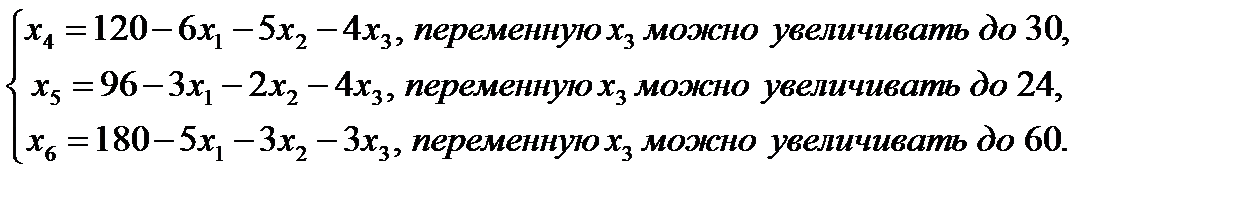
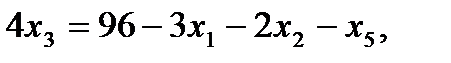
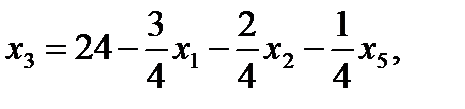
 в
в  ,
,  и целевую функцию.
и целевую функцию.

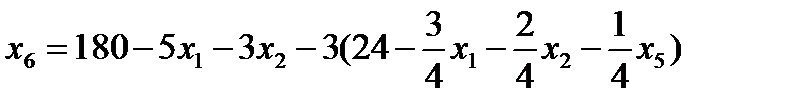
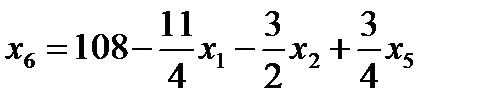
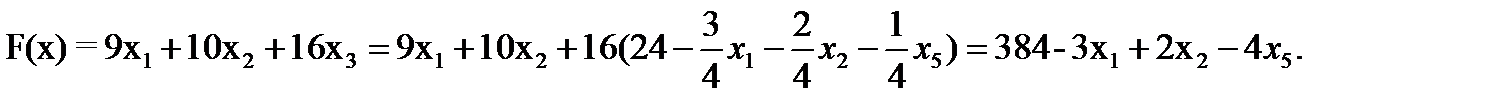
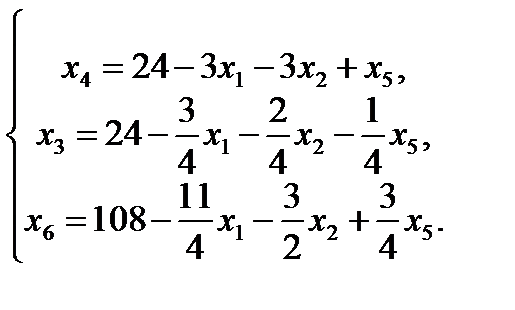
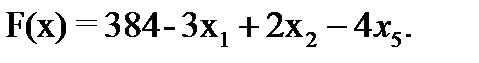
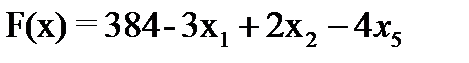 , которую будем увеличивать.
, которую будем увеличивать.
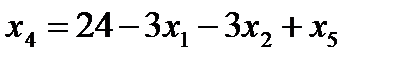
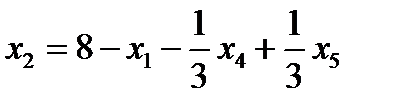
 ,
, 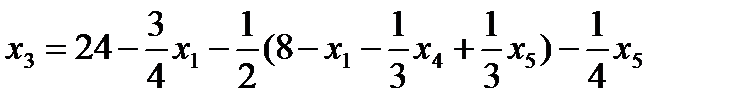
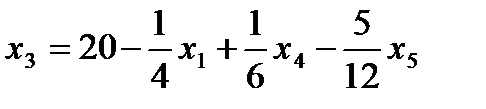
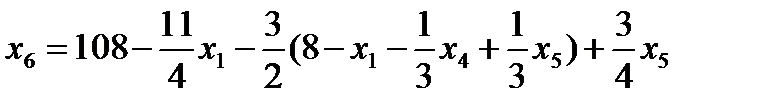
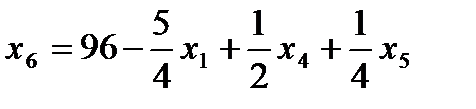
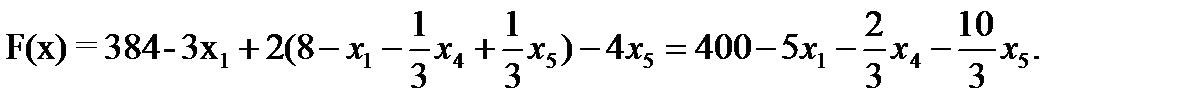
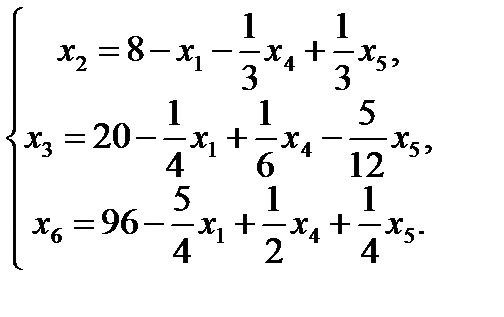
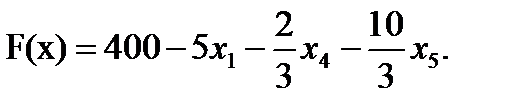
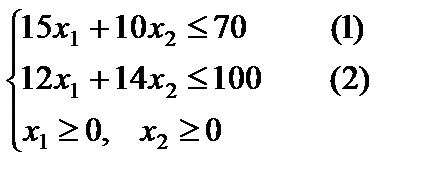
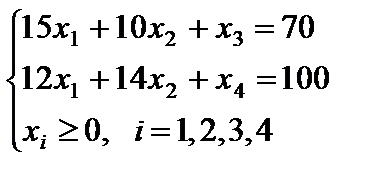









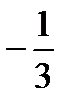

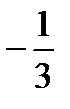







 → max
→ max

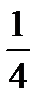


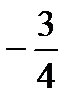

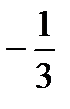








 (6.1)
(6.1) (6.2)
(6.2) (6.3)
(6.3)