
|
|
ГЕОМЕТРИЧЕСКОЕ ИСТОЛКОВАНИЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ12 ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Уральский государственный экономический университет
МЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ ТЕОРИЯ
ВВЕДЕНИЕ В основе любой целенаправленной деятельности лежат процессы принятия решений. В экономике они предшествуют созданию производственных организаций, обеспечивают их оптимальное функционирование и взаимодействие, в научных исследованиях – позволяют выделить важнейшие научные проблемы, найти способы их изучения. При создании новой техники – составляют важный этап в проектировании машин, устройств, приборов; в социальной сфере – используются для организации функционирования и развития социальных процессов, их координации с хозяйственными и экономическими процессами. Оптимальные решения позволяют достигать цели при минимальных затратах трудовых, материальных и сырьевых ресурсов. В классической математике методы поиска оптимальных решений рассматривают в разделах, связанных с изучением экстремумов функций, в математическом программировании. Задачи метода оптимальных решений находят применение в различных областях человеческой деятельности, где необходим выбор одной из возможных программ действий. Значительное число задач, возникающих в обществе, связано с управляемыми явлениями, т. е. с явлениями, регулируемыми на основе сознательно принимаемых решений. При ограниченном объеме информации, который был доступен на ранних этапах развития общества, принималось оптимальное решение на основании интуиции и опыта, а затем, с возрастанием объема информации об изучаемом явлении, – с помощью ряда прямых расчетов. Так происходило, например, создание календарных планов работы промышленных предприятий. Совершенно иная картина возникает, например, на современном промышленном предприятии с многосерийным и многономенклатурным производством, когда объем входной информации столь велик, что его обработка с целью принятия определенного решения невозможна без применения современных электронных вычислительных машин. Под принятием решений в курсе «методы оптимальных решений» понимают сложный процесс, в котором можно выделить следующие основные этапы: 1-й этап. Построение качественной модели рассматриваемой проблемы, т. е. выделение факторов, которые представляются наиболее важными, и установление закономерностей, которым они подчиняются. 2-й этап. Построение математической модели рассматриваемой проблемы, т. е. запись в математических терминах качественной модели. Таким образом, математическая модель – это записанная в математических символах абстракция реального явления. Математическая модель устанавливает соотношения между совокупностью переменных. Этот этап включает также построение целевой функции переменных, т. е. такой числовой характеристики, большему (или меньшему) значению которой соответствует лучшая ситуация с точки зрения принимаемого решения. Итак, в результате этих двух этапов формируется соответствующая математическая задача. 3-й этап. Исследование влияния переменных на значение целевой функции. На данном этапе находят решение соответствующих экстремальных задач. 4-й этап. Сопоставление результатов вычислений, полученных на 3-м этапе, с моделируемым объектом, т. е. экспертная проверка результатов. Таким образом, на этом этапе устанавливается степень адекватности модели и моделируемого объекта в пределах точности исходной информации. Здесь возможны два случая: первый случай. Если результаты сопоставления неудовлетворительны, то переходят ко второму циклу процесса. При этом уточняется входная информация о моделируемом объекте и, в случае необходимости, уточняется постановка задачи или строится заново математическая модель; решается соответствующая математическая задача и, наконец, снова проводится сопоставление. второй случай. Если результаты сопоставления удовлетворительны, то модель принимается. В данном пособии задачи составлены на основе экономико-математических моделей, описывающих поведение различных экономических процессов в линейной форме, что также говорит о возможности их непосредственного применения в экономических исследованиях. 2. ПОСТАНОВКА ЗАДАЧ Математическое программирование представляет собой математическую дисциплину, занимающуюся изучением экстремальных задач и разработкой методов их решения. В общем виде математическая постановка экстремальной задачи состоит в определении наибольшего или наименьшего значения функции
где F и Если F и Если же хотя бы одна функция будет нелинейной, то это задача нелинейного программирования (выпуклого, целочисленного, параметрического, динамического и т.д. программирования). Многие задачи линейного программирования являются математическими моделями разнообразных реальных процессов, наблюдаемых в экономике. Эти методы учитывают только линейные связи между объектами исследования. Среди многочисленных задач линейного программирования можно выделить задачи об использовании сырья, о составлении рациона, о загрузке оборудования, транспортную задачу и т.д. Рассмотрим некоторые из данных задач.
ЗАДАЧА ОБ ИСПОЛЬЗОВАНИИ СЫРЬЯ Предприятие выпускает
Обозначим
Получаем систему ограничений:
Вся выпускаемая продукция есть положительная величина, поэтому Прибыль предприятия от реализации продукции равна:
Такую функцию Получаем математическую модель поставленной задачи. Необходимо среди неотрицательных решений системы ограничений найти такое, которое дает максимальное значение линейной (целевой) функции. Пример 2.1. Мебельный кооператив делает стулья и табуретки. Используется древесина двух сортов (I и II) по 8 единиц каждой. На стул расходуется древесина I и II вида, соответственно 2 и 4 единицы, на табурет расходуется древесина только I вида в количестве 2 единиц. Для того, чтобы сделать стул, надо затратить 4 часа, а на табурет 2 часа. Составить математическую модель задачи: сколько следует изготовлять кооперативу стульев и табуреток, если прибыль от реализации одного табурета 600 рублей, а одного стула 800 рублей. А общее количество затрат труда не менее 12 часов. Решение. Для удобства оформим данные задачи в таблице.
Составим математическую модель задачи. 1. Введем переменные задачи: х1 – количество стульев, планируемых к выпуску; x2 – количество табуреток, планируемых к выпуску. 2. Составим систему ограничений. Ограничения должны учитывать возможности ежедневного потребления сырья и ограниченность спроса на готовую продукцию. Т.е. ограничение на сырье можно записать следующим образом
Из таблицы с данными имеем следующее. Используемое количество древесины I вида равно Используемое количество древесины II вида равно Поскольку ежедневный расход древесины I и II видов ограничен соответственно 8 ед. каждый, получаем следующие ограничения:
Есть еще одно ограничение по количеству затрат труда. Чтобы сделать стул, надо затратить 4 часа, а на табурет 2 часа и известно, что общее количество затрат труда должно быть не менее 12 часов, т.е. К сформулированным выше ограничениям необходимо добавить условие неотрицательности переменных: Окончательно система ограничений будет записана следующим образом:
3. Зададим целевую функцию Целевая функция, как суммарный ежедневный доход, должна возрастать при увеличении ежедневных объемов производства мебели. В соответствии с целями кооператива получаем: F(x) = 800x1 + 600x2 → max
ЗАДАЧА О СОСТАВЛЕНИИ РАЦИОНА Имеется n видов продукции
Обозначим
Минимальная стоимость суточного рациона равна:
Пример 2.2. Фермерское хозяйство при составлении рациона кормления скота использует 2 вида корма: свежее сено и силос. Рацион должен обладать определенной питательностью, измеряемой в кормовых единицах и содержать в необходимых количествах белок, кальций и фосфор: суточный рацион должен содержать не менее 30 кормовых единиц, 1000 г белка, 100 г кальция и 80 г фосфора. В таблице приведены данные о содержании компонентов в 1 кг каждого продукта питания и себестоимость этих продуктов. Составить математическую модель задачи, определяющую оптимальный рацион при минимальной стоимости.
Решение. Составим математическую модель задачи. 1. Введем переменные задачи: х1 – количество свежего сена; x2 – количество силоса. 2. Составим систему ограничений:
3. Зададим целевую функцию: F(X) = 3x1 + 2x2 → min
ЗАДАЧА О МАКСИМАЛЬНОЙ ЗАГРУЗКЕ ОБОРУДОВАНИЯ Пусть имеется m видов оборудования
Обозначим Получаем систему ограничений:
Составим функцию F загрузки оборудования:
целевая функция. Пример 2.3. На трех станках обрабатывается 2 вида изделий B1 и B2. Трудоемкость обработки единицы изделия В1 на каждом станке 4, 0 и 2 единицы времени, соответственно. А изделие В2 – 2, 3 и 2 единицы времени. Фонд полезного времени работы первого станка - 48 часов, второго – 36 часов, а третьего 40. Цена единицы изделия В1 – 150 рублей, изделия В2 – 120 рублей. Найти план производства изделий, обеспечивающий выполнение плана не менее чем на 1200 рублей при наименьшей загрузке оборудования. Решение. Для удобства оформим данные задачи в таблице.
Составим математическую модель задачи. 1. Введем переменные задачи: х1 – количество изделий B1, планируемых к выпуску; x2 – количество изделий B2, планируемых к выпуску. 2. Составим систему ограничений:
3. Зададим целевую функцию: F(X) = (4+0+2)x1 + (2+3+2)x2 → min F(X) = 6x1+7x2 → min
2.1. ФОРМЫ ЗАПИСИ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ Общей задачей ЛП называется задача, которая состоит в определении
При условиях
где Функция (2.1.1) называется целевой функцией задачи (2.1.1) - (2.1.5), а условия (2.1.2) – (2.1.5) – ограничениями данной задачи. Стандартной (симметричной) задачей ЛП называется задача, которая состоит в определении max значения целевой функции (2.1.1), при выполнении условий (2.1.3), (2.1.5), или в определении min значения целевой функции (2.1.1), при выполнении условий (2.1.2), (2.1.5). Канонической (основной) задачей ЛП называется задача, которая состоит в определении max значения целевой функции (2.1.1), при выполнении условий (2.1.4), (2.1.5). Указанные выше три формы записи задач ЛП (общая, симметричная и каноническая) эквивалентны в том смысле, что каждая задача может быть с помощью несложных преобразований переписана в другую форму. Чтобы перейти от одной задачи ЛП к другой нужно уметь:
Для того чтобы перейти от нахождения минимума к нахождению максимума достаточно изменить знаки коэффициентов целевой функции. Например 2. Переходить от неравенств к уравнениям и наоборот. Например дано неравенство Неравенство Пример: Записать задачу ЛП в канонической форме:
ГЕОМЕТРИЧЕСКОЕ ИСТОЛКОВАНИЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ Графический метод используется для решения задач с двумя переменными следующего вида:
Геометрический метод не является общим методом решения задач ЛП. Он выполняет лишь вспомогательную роль и позволяет наглядно представить себе свойства задачи ЛП и ее решение симплекс-методом. Пару неизвестных Тогда множеству допустимых решений задачи в плоскости Определим вид этой области. Каждое из неравенств системы (3.2) заменим на прямую Для того чтобы выяснить какая полуплоскость нам нужна необходимо взять любую точку M из любой полуплоскости (не на граничной прямой) и подставляем координаты точки в неравенство. Если неравенство верно, то полуплоскость, которой принадлежит точка М, является искомой. Если неравенство оказалось неверным, то следует выбрать противоположную полуплоскость. Очевидно, что решением системы (3.2) будут точки, принадлежащие всем неравенствам одновременно. Совокупность этих точек называется многоугольником решений. Множество называется выпуклым, если с любыми двумя точками a и b, принадлежащими множеству оно содержит и отрезок Точка N выпуклого множества называется вершиной, если она не является внутренней точкой какого-либо отрезка принадлежащего множеству. Т.к. допустимая область решений состоит из пересечения выпуклых множеств (полуплоскостей) то, очевидно, что многоугольник решений будет выпуклым множеством или пустым. Рассмотрим поведение целевой функции (3.1) При фиксированном значении Вектор Вектор Теорема. Если основная задача ЛП имеет решение, то max (min) значение целевая функция задачи принимает в одной из вершин многоугольника (многогранника) решений. Если max (min) значение целевая функция задачи принимает более чем в одной вершине, то она принимает его на прямой (или на отрезке).
Этапы решения задачи ЛП геометрическим методом: 1. Построить граничные прямые,соответствующие данным ограничениям-неравенствам из системы (3.2). 2. Найти полуплоскости, определяемые каждым из ограничений системы (3.2). 3. Найти многоугольник решений. 4. Построить вектор 5. Построить прямую 6. Передвинуть прямую 7. Определить координаты точки максимума функции и вычислить значение целевой функции в этой точке. Пример 3.1. Для изготовления двух видов изделий I и II используются три вида сырья. На производство единицы изделия I требуется затратить сырья первого вида 13 кг, сырья второго вида – 32 кг, сырья третьего вида – 58 кг. На производство единицы изделия II требуется затратить сырья первого вида 24 кг, сырья второго вида – 32 кг, сырья третьего вида – 29 кг. Производство обеспечено сырьем первого вида в количестве 312 кг, сырьем второго вида – 480 кг, сырьем третьего вида – 696 кг. Прибыль от реализации единицы готового изделия I вида составляет 4 усл. ед, а изделия II вида – 3 усл. ед. Требуется составить план производства изделий I и II, обеспечивающий максимальную прибыль от их реализации, если заранее планируется изготовление не менее 10 единиц изделий I и II. Решение: Для удобства оформим данные задачи в таблице.
Составим математическую модель задачи. 1. Введем переменные задачи: х1 – количество изделий вида I, планируемых к выпуску; x2 – количество изделий вида II, планируемых к выпуску. 2. Составим систему ограничений:
3. Зададим целевую функцию: F(X) = 4x1 + 3x2 → max Построим область допустимых решений задачи. Для этого в прямоугольной декартовой системе координат построим прямую l1: 13x1+24x2=312, соответствующую ограничению (1). Для этого найдем координаты двух точек, принадлежащих данной прямой. Полагаем x1=0, тогда x2 = 13, возьмем x2 = 0, получаем x1=24. Получили координаты точек В (24, 0) и С (0, 13). Определим, какая из двух полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (1). Для этого подставим, например, координаты точки О (0; 0), не лежащей на прямой l1, в данное ограничение: 13·0 + 24·0 ≤ 312. Получаем 0 ≤ 312, следовательно точка О лежит в полуплоскости решений. Укажем данную полуплоскость штриховкой (рис.1).
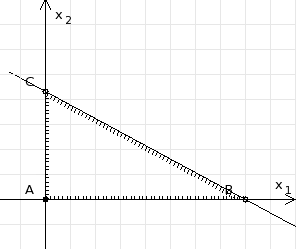
рис. 1 Аналогично строим прямую l2: 32x1+32x2 = 480, соответствующую ограничению (2) , находим полуплоскость решений. Отметим штриховкой общую часть полуплоскостей решений (рис. 2).
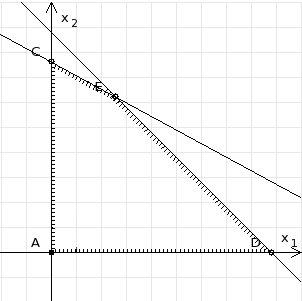
рис. 2 Строим прямую l3: 58x1 + 29x2 = 696, соответствующую ограничению (3), находим полуплоскость решений. Штриховкой обозначим общую часть полуплоскостей решений (рис. 3).
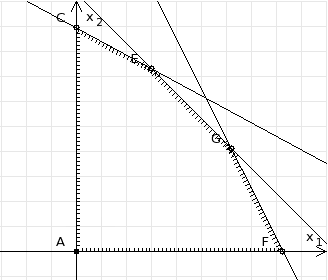
рис. 3 Построим прямую l4: x1+x2 = 10. Определим, какая из двух полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (4). Для этого подставим, например, координаты точки О (0; 0), не лежащей на прямой l4, в данное ограничение. Получаем 0 ≥ 10, следовательно точка О не принадлежит полуплоскости решений. Штрихуем ту часть плоскости относительно прямой, где не лежит точка О. Далее находим общую часть полуплоскостей решений, учитывая при этом условия неотрицательности переменных. Полученную область допустимых решений отметим штриховкой (рис. 4).
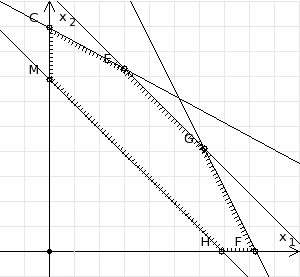
рис. 4 Построим нормаль линий уровня Так как решается задача на нахождение максимума целевой функции, то линию уровня перемещаем в направлении нормали до последней точки многоугольника решений MCEGF (рис. 5).
рис. 5 Видим, что последней точкой данного прямоугольника будет точка G. В данной точке значение функции будет наибольшим. Для нахождения координат точки G = l2 ∩ l3 необходимо решить систему уравнений
Получим G(9, 6). Находим F(G) = 4·9 + 3·6 = 54. Ответ: Для получения максимальной прибыли 54 усл. ед, необходимо производить 9 изделий вида I и 6 изделий вида II. Пример 3.2. Фирма по производству строительных материалов ООО «Вазелло» выпускает два вида стройматериалов: жидкое стекло и пенопласт. Трудозатраты на производство 1 т. стекла – 20 ч, пенопласта – 10 ч. В кооперативе работают 10 рабочих по 40 ч. в неделю. Оборудование позволяет производить не более 15 т. стекла и 30 т. пенопласта в неделю. Прибыль от реализации 1 т. жидкого стекла 50 тыс. руб.; 1 т. пенопласта – 40 тыс. руб. Сколько стройматериалов каждого вида следует выпускать кооперативу для получения максимальной прибыли? Решение: Составим математическую модель задачи. 1. Введем переменные задачи: х1 – объем производства жидкого стекла в неделю; x2 – объем производства пенопласта в неделю. 2. Составим систему ограничений:
3. Зададим целевую функцию: F(X) = 50x1 + 40x2 → max Построим прямые Получаем область допустимых решений - пятиугольник AFGED (рис. 6).
рис. 6
Построим вектор В нашем случае, касание линии уровня, перед выходом из области допустимых решений, произойдет в точке G = l1 ∩ l3. В данной точке значение функции будет наибольшим. Найдем координаты точки G. Решив систему Ответ: производство 5 т. жидкого стекла и 30 т. пенопласта в неделю, обеспечивает ООО «Вазелло» максимальную прибыль, равную 1450000 рублей.
Пример 3.3. (о составлении рациона). Фармацевтическая фирма «Ozark» ежедневно производит 800 фунтов некой пищевой добавки – смеси кукурузной и соевой муки, состав которой представлен в следующей таблице.
Диетологи требуют, чтобы в пищевой добавке было не менее 30% белка и не более 5% клетчатки. Фирма «Ozark» хочет определить рецептуру смеси минимальной стоимости с учетом требований диетологов. Решение. Составим математическую модель задачи. 1. Введем переменные задачи: х1 – количество (в фунтах) кукурузной муки, используемой в производстве пищевой добавки; x2 – количество (в фунтах) кукурузной муки, используемой в производстве пищевой добавки. 2. Составим систему ограничений. Ограничение 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 при условиях
при условиях ,
, - заданные функции, а
- заданные функции, а  - некоторые действительные числа.
- некоторые действительные числа. – линейные функции, то решается задача линейного программирования (ЛП).
– линейные функции, то решается задача линейного программирования (ЛП). видов продукции
видов продукции  ,используя при этом
,используя при этом  -видов сырья
-видов сырья  запасы которого равны соответственно
запасы которого равны соответственно 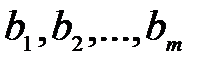 . На каждый
. На каждый  вид продукции используется
вид продукции используется  вида сырья в количестве
вида сырья в количестве  , единиц. Каждый вид продукции
, единиц. Каждый вид продукции  приносит предприятию прибыль
приносит предприятию прибыль  . Требуется составить такой план производства, чтобы прибыль от его реализации была максимальной, при имеющихся запасах сырья.
. Требуется составить такой план производства, чтобы прибыль от его реализации была максимальной, при имеющихся запасах сырья.




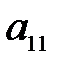




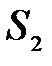





















 - кол-во выпускаемой продукции каждого вида. Тогда для сырья
- кол-во выпускаемой продукции каждого вида. Тогда для сырья  расход будет следующий:
расход будет следующий: и т.д.
и т.д.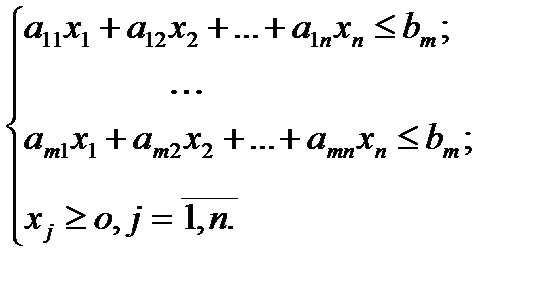
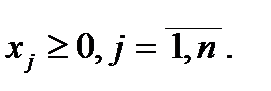
 .
. называют целевой функцией.
называют целевой функцией.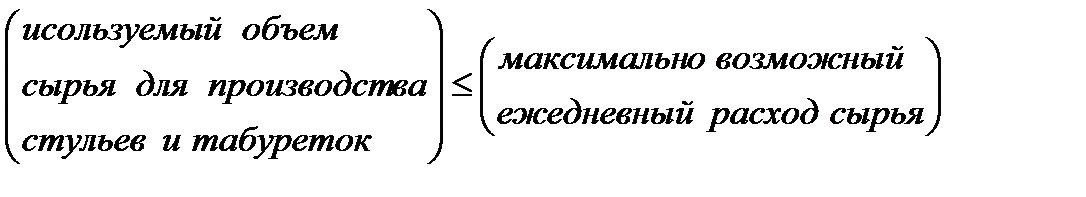
 (ед),
(ед), (ед).
(ед).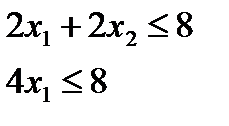

 .
. .
.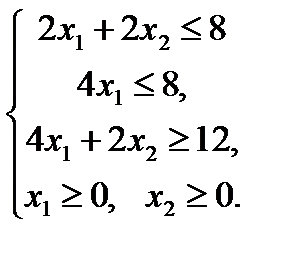
 по цене за единицу продукции соответственно
по цене за единицу продукции соответственно  . В продукции содержатся питательные вещества
. В продукции содержатся питательные вещества  . Известна суточная потребность организма в питательном веществе
. Известна суточная потребность организма в питательном веществе  , она должна быть не менее
, она должна быть не менее  . Требуется составить суточный рацион n видов продукции, который будет иметь минимальную стоимость, если известно, что в
. Требуется составить суточный рацион n видов продукции, который будет иметь минимальную стоимость, если известно, что в  виде продукции содержится питательного вещества
виде продукции содержится питательного вещества  в количестве
в количестве  единиц.
единиц.






























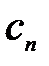
 - кол-во продуктов, входящих в рацион. Тогда суточная потребность в питательном веществе
- кол-во продуктов, входящих в рацион. Тогда суточная потребность в питательном веществе  должна быть не менее
должна быть не менее  :
: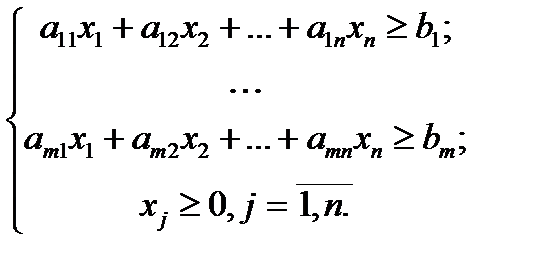
 - целевая функция.
- целевая функция.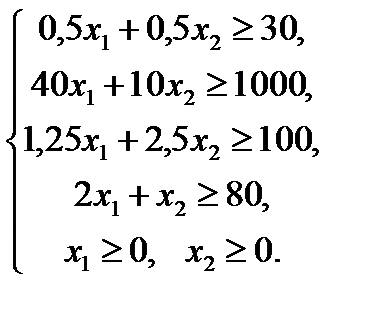
 с помощью которых обрабатываются изделия вида
с помощью которых обрабатываются изделия вида  . Известен фонд полезного времени оборудования
. Известен фонд полезного времени оборудования  . Требуется рассчитать план выпуска изделий, обеспечивающий максимальную загрузку оборудования, если известно, что при изготовлении одной единицы изделия вида
. Требуется рассчитать план выпуска изделий, обеспечивающий максимальную загрузку оборудования, если известно, что при изготовлении одной единицы изделия вида  требуется времени на оборудовании
требуется времени на оборудовании  в количестве
в количестве  единиц.
единиц.

















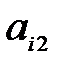









 - кол-во единиц выпускаемой продукции каждого вида
- кол-во единиц выпускаемой продукции каждого вида  . Тогда расход времени оборудования
. Тогда расход времени оборудования  будет следующим:
будет следующим:  и т.д.
и т.д.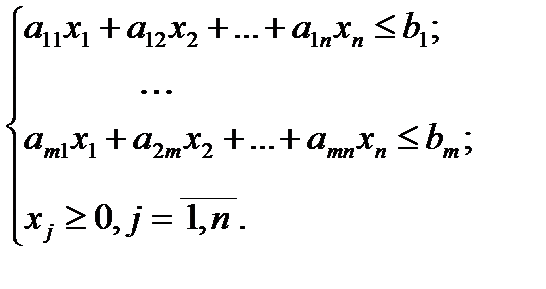
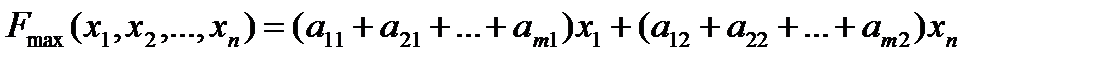

 (2.1.1)
(2.1.1)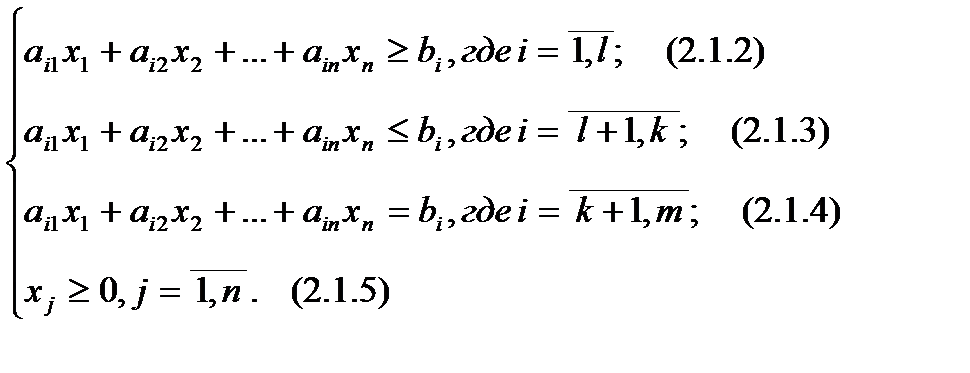
 ,
, 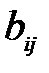 , и
, и  - заданные постоянные величины.
- заданные постоянные величины. , тогда
, тогда  .
. , тогда
, тогда 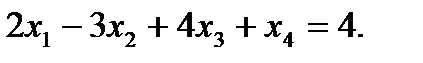
 , тогда
, тогда  .
.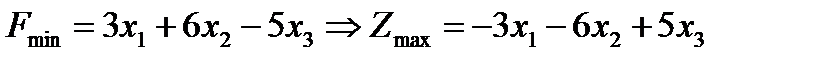


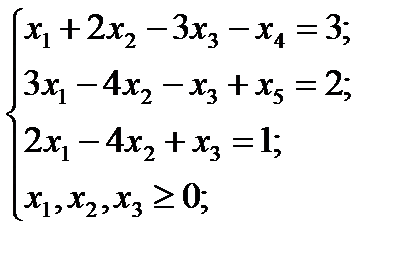
 (3.1)
(3.1) (3.2)
(3.2) и
и  рассмотрим как координаты точек плоскости в которой определена декартова система координат с осями
рассмотрим как координаты точек плоскости в которой определена декартова система координат с осями  и
и  . Множество пар значений
. Множество пар значений  , удовлетворяющих системе (3.2) называется множеством допустимых решений задачи ЛП.
, удовлетворяющих системе (3.2) называется множеством допустимых решений задачи ЛП. будет отвечать некоторая область.
будет отвечать некоторая область. ,
,  . Это будет граничная прямая, делящая плоскость на две части (на две полуплоскости).
. Это будет граничная прямая, делящая плоскость на две части (на две полуплоскости). , их соединяющий.
, их соединяющий. .
. целевая функция определяет на плоскости прямую линию
целевая функция определяет на плоскости прямую линию  При изменении F получим семейство параллельных прямых, называемых, линиями уровня.
При изменении F получим семейство параллельных прямых, называемых, линиями уровня. называется целевым вектором или вектором направлений.
называется целевым вектором или вектором направлений.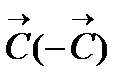 показывает направление наибольшего возрастания (убывания) целевой функции.
показывает направление наибольшего возрастания (убывания) целевой функции. .
. , проходящую через многоугольник решений.
, проходящую через многоугольник решений. в направлении вектора
в направлении вектора  .
.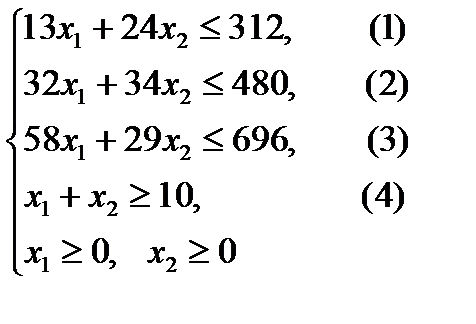
 и одну из линий, например 4x1 + 3x2 = 0.
и одну из линий, например 4x1 + 3x2 = 0.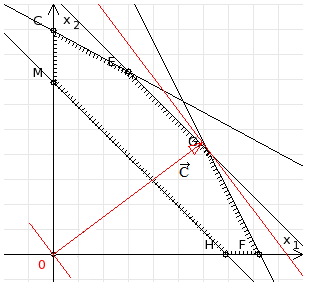
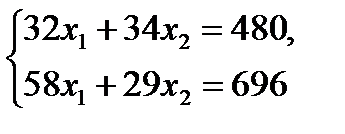
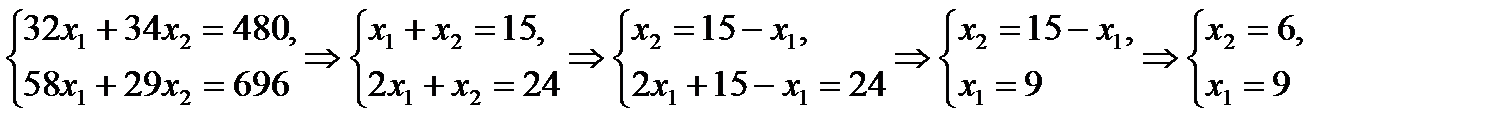
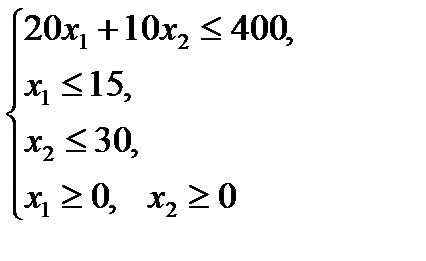
 соответствующие данным неравенствам.
соответствующие данным неравенствам.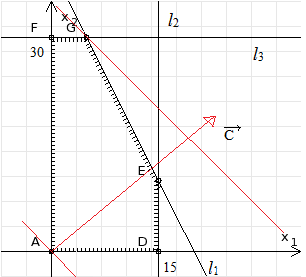
 . Затем линию уровня перемещаем в направлении нормали до последней точки многоугольника решений.
. Затем линию уровня перемещаем в направлении нормали до последней точки многоугольника решений. находим x1=5, x2=30, F(X) = 1450.
находим x1=5, x2=30, F(X) = 1450.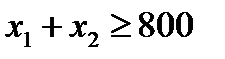 описывает то условие, что фирма должна выпускать не менее 800 фунтов в день.
описывает то условие, что фирма должна выпускать не менее 800 фунтов в день.