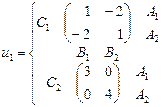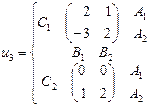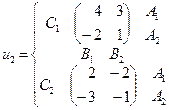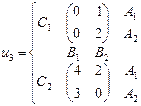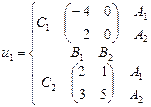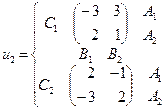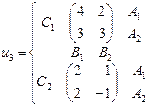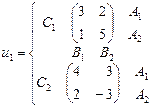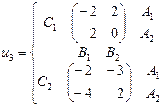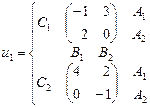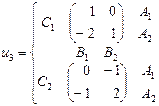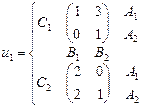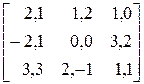|
|
Раздел 3. Индивидуальные занятия12 Задание по теме «Статические игры с полной информацией» 1. Каждый из двух игроков (i=1,2) имеет по три стратегии: a,b,c и x,y,z соответственно. Взяв своё имя как бесконечную последовательность символов типа иваниваниваниван…., задайте выигрыши первого игрока так: u1(a,x)=”и”, u1(a,y)=”в”, u1(a,z)=”а”, u1(b,x)=”н”, u1(b,y)=”и”, u1(b,z)=”в”, u1(c,x)=”а”, u1(c,y)=”н”, u1(c,z)=”и”. Подставьте вместо каждой буквы имени её порядковый номер в алфавите, для чего воспользуйтесь таблицей: Таблица 4. Числовые коды символов русского алфавита
Аналогично используя фамилию, задайте выигрыши второго игрока, u2( ). а) Есть ли в вашей игре доминирующие и строго доминирующие стратегии? Если есть, то образуют ли они равновесие в доминирующих стратегиях? б) Каким будет результат последовательного отбрасывания строго доминируемых стратегий? в) Найдите равновесия Нэша этой игры, в том числе в смешанных стратегиях (если они существуют). 2. Составьте по имени, фамилии и отчеству игру трех игроков, у каждого из которых по две стратегии (0 или 1), по тому же принципу, как и в задаче 1. Ответьте на те же вопросы, что и в п. 1. Например, у студента, имя, отчество и фамилия которого Конрад Карлович Михельсон, выигрыши в буквенном выражении запишутся так:
а в числовой форме они имеют следующий вид:
Задание по теме «Повторяющиеся игры» Имеется следующая матрица, аналогичная матрице игры «Дилемма заключенного»:
Значение а равно остатку от деления суммы кодов букв имени студента на 10, значение b равно 10 плюс остаток от деления суммы кодов букв отчества студента на 10, а значение с равно 20 плюс остаток от деления суммы кодов букв фамилии студента на 10. Построить в нормальной форме игру с двумя повторениями исходной игры и определить в этой игре все равновесия Нэша и показать, какие из них будут совершенными в подыграх равновесиями Нэша (СПРН).
Задание по теме «Статические игры с неполной информацией» Рассмотреть игру «Выбор компьютера» с неполной информацией, где значения полезностей (выигрыши) игроков следует расставить в соответствии с кодами личных данных студента:
Значение а равно 20 плюс остаток от деления суммы кодов букв имени студента на 10, значение b равно остатку от деления суммы кодов букв отчества студента на 10, а значение с равно 10 плюс остаток от деления суммы кодов букв фамилии студента на 10. Исследовать каждый исход игры на предмет того, будет ли он равновесным по Байесу–Нэшу, и если да, то при каких значениях вероятностей π наличия любителей IBM.
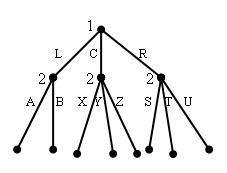
Раздел 4. Задания к зачету Варианты 1–20. В статической игре с полной информацией трех игроков игрок 1 выбирает стратегию из множества
Варианты 21 – 30. В следующей статической игре с полной информацией найти все равновесия Нэша, в том числе в смешанных стратегиях.
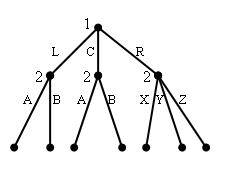
Варианты 31 – 40. В следующий схемах динамических игр с полной информацией (см. рисунки 1-4) выигрыши игроков взять из статических игр вариантов 21–30 соответственно. Провести процесс обратной индукции, представить игру в нормальной форме и найти в ней все совершенные в подыграх равновесия Нэша.
Рис. 1. Схема вариантов 31-33
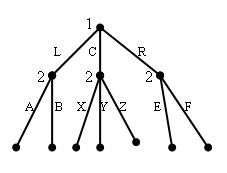
Рис. 2. Схема вариантов 34-36
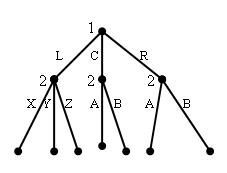
Рис. 3. Схема вариантов 37,38
Рис. 4. Схема вариантов 39,40 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
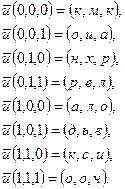

 , игрок 2 – из множества
, игрок 2 – из множества  , а игрок 3 – из множества
, а игрок 3 – из множества  . Найти множество равновесий Нэша, если функции выигрыша игроков заданы следующими парами матриц:
. Найти множество равновесий Нэша, если функции выигрыша игроков заданы следующими парами матриц: