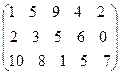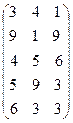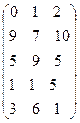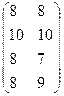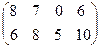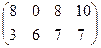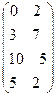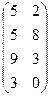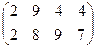|
|
Раздел 1. Практические занятия12 Кафедра статистики и эконометрики Методическая разработка по дисциплине «Теория игр в экономике» для проведения практических занятий, самостоятельной и индивидуальной работы студентов, обучающихся по направлению 080100.62 «Экономика» и по специальности 080105.65 «Финансы и кредит» (с сокращенным сроком обучения)
Казань 2009 Составитель: к.т.н., доцент Костромин А.В. Рецензент: д.т.н., профессор Исмагилов И.И.
Обсуждена на заседании кафедры статистики и эконометрики 24 февраля 2009 г, протокол № 7.
Контроль качества: методист: доцент Белоглазова Л.П. ст. методист: доцент Калинина Т.Н. начальник отдела У и ККО: доцент Андреева Р.Н. Введение В последние три десятилетия наблюдается стремительное повышение интереса к теории игр и значительное возрастание ее роли. Без нее в настоящее время уже немыслима современная экономическая теория, причем область применения теории игр постоянно расширяется. С экономической точки зрения суть теории игр в том, чтобы помочь экономистам понимать и предсказывать то, что может происходить в экономических ситуациях, и сейчас вряд ли можно найти область экономики, где основные концепции теории игр не были бы необходимыми для понимания современной экономической литературы. Данная методическая разработка способствует системному изучению дисциплины «Теория игр в экономике» студентами, обучающимися по направлению 080100.62 «Экономика» и по специальности 080105.65 «Финансы и кредит» (с сокращенным сроком обучения) и включает вопросы для обсуждения, практические задания, контрольные вопросы и задания для самостоятельной работы студентов, список литературы. Практические занятия по данной дисциплине проводятся с целью изучения и усвоения студентами теоретических вопросов, связанных с применением теории игр к различным вопросам экономики. Уровень усвоения студентами теоретического материала проверяется посредством опроса по основным вопросам темы. Решение задач в рамках практических занятий позволяет студентам применить теоретические знания, полученные на лекциях, к анализу различных ситуаций в играх в условиях конфликта или несовпадения интересов. Контрольные вопросы и задания предназначены для проверки качества усвоения лекционного материала. Ответы на контрольные вопросы и задания готовятся студентами самостоятельно и проверяются преподавателями на практических занятиях. Задания для самостоятельной работы призваны закрепить полученные технические навыки решения типовых задач, разобранных на практических занятиях. Задания для индивидуальной работы направлены на углубление практической подготовки студентов и составлены по индивидуальным данным студентов. Они охватывают статические игры с полной информацией, повторяющиеся игры и статические игры с неполной информацией. Выполнение индивидуальных заданий завершается составлением отчета в соответствии с приведенными в данных методических указаниях требованиями. В конце методических указаний даются задания, предъявляемые студентам при сдаче зачета по дисциплине. Раздел 1. Практические занятия Тема 1. Введение в теорию игр (2 занятия) Занятие 1 Вопросы для обсуждения 1. Предмет теории игр и его история. Теория Неймана-Моргенштерна. 2. Поведение субъекта в условиях несовпадения интересов (конфликта). 3. Принятие оптимального решения в условиях конфликта. Практические задания 1. Каждый из двух партнеров, не зная хода другого, называет цифру 1 или 2, причем при совпадении названных цифр второй платит первому одну единицу выигрыша, а в противном случае второй получает от своего противника столько же. Представить игру в матричной форме и пояснить, как влияет решение, принимаемое каждым игроком, на поведение партнера. 2. Игроки выбирают целые числа от 1 до k. Если первый выбрал х, а второй у, то первый получает (х-у) единиц выигрыша, если х≥у, и платит (х+у) единиц выигрыша, если х<у. Рассмотреть случай, когда k=5. Представить игру в матричной форме и определить наиболее выгодные с точки зрения выигрыша ходы игроков. 3. Первый игрок называет одно их чисел 1 или 2, а второй – одно из чисел 1, 2, 3. При этом каждый их партнеров пытается угадать, какое из чисел назовет противник. Если оба партнера угадали или ошиблись одновременно, то игра заканчивается вничью. Если же угадал один из них, то он получает выигрыш, равный числу, названному противником. Представить игру в матричной форме и определить наиболее выгодную тактику каждого игрока с учетом многократного повторения игры. Задания для самостоятельной работы 1. Изучить основные способы формализации предпочтений игроков и функций их полезности. 2. Сформулировать теорему об ожидаемой полезности. 3. Показать, как формулируется полезность денег. 4. Изложить основные положения теории Сэвиджа.
Занятие 2 Вопросы для обсуждения 1. Классификация игр: по характеру получения информации, по виду функции выигрыша, по количеству игроков и стратегий. 2. Развернутая и нормальная формы представления игры. 3. Связь матричной и нормальной форм. Практические задания 1. Предприятие выпускает скоропортящуюся продукцию, которую оно может сразу отправить потребителю (стратегия А), отправить на склад для хранения (стратегия Б) или подвергнуть дополнительной обработке (стратегия В) для длительного хранения. В свою очередь, потребитель может немедленно приобрести эту продукцию (стратегия I), приобрести ее в течение небольшого отрезка времени (II) или затребовать ее после длительного периода времени (III). Если предприятие выберет стратегию А, то дополнительные затраты на хранение и обработку продукции не потребуются. Однако, если при этом потребитель применит стратегию II или тем более III, то предприятие потерпит убытки из-за порчи части продукции. Наоборот, если предприятие выберет стратегию В, а потребитель – стратегию I, то возникнут неоправданные расходы на консервацию продукции. Определить оптимальное соотношение между продукцией, отправляемой потребителю на склад и на дополнительную обработку, руководствуясь «минимаксным критерием» (гарантированный средний уровень убытка), при следующей матрице затрат:
2. Для отопления помещения необходимо приобрести топливо. Однако расход топлива и цены на него зависят от погоды в зимнее время (мягкая, нормальная или суровая зима; см. таблицу): Таблица 1. Потребность в топливе и его цена
В настоящее время уголь может быть приобретен по минимальной цене (10 ден.ед./т), и неиспользованный излишек угля можно реализовать весной по цене 5 ден.ед./т. Можно избрать одну из трех стратегий в закупке угля: 5 т, 10 т и 18 т. Предполагая, что подобных помещений имеется 100, определить оптимальную стратегию в образовании запасов, руководствуясь «минимаксным критерием». 3. Магазин может завезти в различных пропорциях товары трех типов (А, Б и В). Их реализация, а следовательно, и получаемая магазином прибыль зависят от вида товара и состояния спроса. Предполагая, что последний может характеризоваться тремя состояниями (I, II, III) и учитывая, что спрос связан с изменением моды и прогнозирование его невозможно, определить оптимальные пропорции в закупке товаров из условия средней гарантированной прибыли при следующей матрице прибылей:
Контрольные вопросы 1. Что такое ход игрока? 2. Что такое стратегия игрока и чем она отличается от хода? 3. Что называют информационным множеством игрока? 4. В чем состоит задача теории игр? 5. Что является решением игры? Задания для самостоятельной работы 1. Выполнить задание 1 из раздела 2. 2. Выполнить задание 2 из раздела 2. 3. Выполнить задание 3 из раздела 2. Рекомендуемая литература 1. Акимов В.П. Основы теории игр: учеб. пособие / - М.: МГИМО – Университет, 2008.- С.3-5, 8-21. 2. Данилов В.И.Лекции по теории игр: учеб. пособие / - М.: РЭШ, 2002.- C. 7-13, 19-23, 29-32. 3. Меньшиков И.С. Лекции по теории игр и экономическому моделированию. – М.: МЗ Пресс, 2007.- С. 10-11, 30-31. 4. Печерский С.Л., Беляева А.А. Теория игр для экономистов. Вводный курс: учебное пособие – Спб.: Европейский университет, 2001.- C. 9-12, 23-28. Тема 2. Статические игры с полной информацией (1 занятие) Вопросы для обсуждения 1. Определение статистических игр с полной информацией. 2. Доминирование стратегий, строгое доминирование, равновесие в доминирующих стратегиях. Последовательное исключение строго доминируемых стратегий. 3. Равновесие Нэша. 4. Существование равновесия Нэша и смешанные стратегии. Вычисление равновесия Нэша в смешанных стратегиях. Практические задания 1. Три игрока выбирают одну из трех альтернатив: А,В или С. Альтернатива выбирается по правилу простого большинства. Каждый из игроков голосует только за одну альтернативу. Если ни одна из альтернатив не наберет большинства, то будет выбрана альтернатива А. выигрыши игроков в зависимости от выбранной альтернативы следующие:
Найти в этой игре все равновесия Нэша. 2. Формируются два избирательных блока, которые будут претендовать на места в законодательном собрании города. Каждый из блоков может выбрать одну из трех ориентаций: «левую» (L), «правую» (R) или «экологическую» (E). Каждая из ориентаций может привлечь 50%, 30% и 20% избирателей соответственно. Известно, что если интересующая их ориентация не представлена на выборах, то избиратели из соответствующей группы не будут голосовать. Если блоки выберут одну и ту же ориентацию, то голоса соответствующей группы избирателей разделятся поровну между ними. Цель каждого блока – получить наибольшее количество голосов. Составить матрицу игры и найти все равновесия Нэша. 3. Два игрока играют в следующую игру. Каждый называет один из трех предметов: «камень», «ножницы» или «бумага». Игрок, назвавший камень, побеждает игрока, назвавшего ножницы (ножницы тупятся о камень), игрок, назвавший ножницы, побеждает игрока, назвавшего бумагу (ножницы режут бумагу), а игрок, назвавший бумагу, побеждает игрока, назвавшего камень (камень можно завернуть в бумагу). Выигравший игрок получает 1, проигравший получает –1. Если названные предметы совпали, то каждый игрок получает 0. Найти все равновесия Нэша, в том числе в смешанных стратегиях. Контрольные вопросы 1. Как графически отображаются выигрыши покупателей и продавцов при конкурентном равновесии? 2. Что называют рыночной силой участников рынка? 3. В чем состоят задачи участников рынка с точки зрения теории игр? 4. Как записываются выигрыши игроков в дуополии Курно? 5. Что такое условия первого порядка и какую роль они играют в поиске равновесия Нэша? 6. Что такое функция наилучшего ответа игрока на действия партнеров? 7. Как определяется равновесие Нэша в терминах функций отклика? 8. Как учитывается чувствительность к цене конкурента в выигрыше игрока в дуополии Бертрана? 9. Как интерпретируется равновесие Нэша в дуополии Бертрана? Задания для самостоятельной работы 1. Выполнить задание 4 из раздела 2. 2. Изучить основные теоретико-игровые подходы к арбитражным механизмам на рынке труда. 3. Рассмотреть противоречие между индивидуальной и коллективной рациональностью на примере проблемы общин.
Рекомендуемая литература 1. Акимов В.П. Основы теории игр: учеб. пособие / - М.: МГИМО – Университет, 2008.- С. 22-37, 59-80. 2. Данилов В.И.Лекции по теории игр: учеб. пособие / - М..: РЭШ, 2002.- С. 24-28, 33-44. 3. Меньшиков И.С. Лекции по теории игр и экономическому моделированию. – М.: МЗ Пресс, 2007.- С. 9-55. 2. Печерский С.Л., Беляева А.А. Теория игр для экономистов. Вводный курс: учебное пособие – Спб.: Европейский университет, 2001.- С. 30-55, 57-78. Тема 3. Динамические игры с полной информацией (1 занятие) Вопросы для обсуждения 1. Полная и совершенная информация. 2. Алгоритм обратной индукции. 3. Нормальная и развернутая формы представления динамической игры. 4. Совершенное в подыграх равновесие Нэша. Практические задания 1. Пираты делят добычу. У пиратов корабля есть строгая иерархия. Ранг 1 имеет самый «крутой» пират (капитан), ранг 2 - следующий по свирепости пират и т.д. Ранг Как вы думаете, позиция капитана при такой процедуре дележа является сильной или слабой? Запишите свой прогноз до детального исследования игры. Найдите дележ с помощью обратной индукции. Совпал ли ваш прогноз с тем, что получилось в пункте (б)? 1. Предположим, что в последовательных переговорах с бесконечным числом периодов игроки имеют различные факторы дисконтирования:
игроку 2, и тот соглашается. 2. Три олигополиста действуют на рынке с обратной функцией спроса Контрольные вопросы 1. Сколько стратегий имеют игроки в двухходовой динамической игре? 2. Как рациональность игроков проявляется в выборе ходов? 3. Что такое чистая стратегия игрока в динамической игре с полной информацией? 4. Как определяются информационные множества игроков в динамической игре с полной информацией? 5. Что такое подыгра? 6. Чем отличаются равновесие Нэша и совершенное в подыграх равновесие Нэша? 7. Что означают равновесия пустых угроз? 8. Как формируется требование динамической согласованности? 9. Что такое собственная подыгра? 10. Как практически выбрать из всего множества равновесий Нэша совершенные в подыграх равновесие Нэша? Задания для самостоятельной работы 1. Изучить подходы Штакельберга и Гермейера к двухходовой игре. 2. Сформулировать общую модель динамической игры с полной и совершенной информацией. 3. Рассмотреть критику алгоритма обратной индукции. Рекомендуемая литература 1. Акимов В.П. Основы теории игр: учеб. пособие / - М.: МГИМО – Унверситет, 2008.- С. 80-92. 2. Меньшиков И.С. Лекции по теории игр и экономическому моделированию. – М.: МЗ Пресс, 2007.- С. 44-55. 3. Печерский С.Л., Беляева А.А. Теория игр для экономистов. Вводный курс: учебное пособие – Спб.: Европейский университет, 2001.- С. 83-105.
Тема 4. Повторяющиеся игры (2 занятия) Занятие 1 Вопросы для обсуждения 1. Игры с конечным числом повторений. 2. Бесконечно повторяющиеся игры. 3. Народная теорема и ее следствия.
Практические задания 1. Игра с одновременным выбором ходов (см. таблицу 2) повторяется дважды, причем решение, выбранное на первом шаге, становится известным до начала второго шага. Дисконтирование отсутствует. Переменная x больше 4, так что (4,4) не является равновесием в одношаговой игре. Для каких значений x следующая стратегия для каждого игрока соответствует совершенному по подыграм равновесию Нэша? Указание: играем Таблица 2. Матрица выигрышей игроков в задании 1
2. Игра с одновременным выбором ходов (приводимая ниже в таблице 3) повторяется дважды, причем исход первого шага становится известным до начала второго шага. Дисконтирование отсутствует. Можно ли достичь выигрышей (4, 4) на первом шаге при совершенном по подыграм равновесии Нэша в чистых стратегиях? Если это возможно, то опишите стратегию, реализующую это. Если нет, то объясните, почему.
Таблица 3 Матрица выигрышей игроков в задании 2.
Занятие 2 Вопросы для обсуждения 1. Сговор в олигополии Курно. 2. Модель эффективной зарплаты. 3. Денежная политика государства и корпорации. Практические задания 1. Вспомним статическую модель дуополии Бертрана (с однородным продуктом): фирмы объявляют цены одновременно; спрос для фирмы 2. Предположим, спрос изменяется случайно в бесконечно повторяющейся игре Бертрана: в каждом периоде спрос равен
Контрольные вопросы 1. Как определяются стратегии игроков в двукратном повторении дилеммы заключенного? 2. Какая связь существует между равновесием Нэша в статической игре и совершенным в подыграх равновесием Нэша в повторяющейся исходной статической игре? 3. Что такое релейная стратегия? 4. Что означает наказание игрока за отклонение от равновесной релейной стратегии? 5. В чем смысл народной теоремы? 6. Какая связь между совместными смешанными стратегиями и кооперативными траекториями в повторяющейся игре? Задания для самостоятельной работы 1. Изучить кооперативное поведение игроков в повторяющихся играх. 2. Сформулировать понятие равновесия в совместных смешанных стратегиях. 3. Сформулировать арбитражную схему Нэша. 4. Определить смысл стабильности на основе угроз. 5. Выполнить задание 5 из раздела самостоятельной работы. Рекомендуемая литература 1. Акимов В.П. Основы теории игр: учеб. пособие / - М.: МГИМО – Университет, 2008.- С.99-116. 2. Данилов В.И.Лекции по теории игр: учеб. пособие / - М.: РЭШ, 2002.- С.85-91. 3. Меньшиков И.С. Лекции по теории игр и экономическому моделированию. – М.: МЗ Пресс, 2007.- С.85-105. 4. Печерский С.Л., Беляева А.А. Теория игр для экономистов. Вводный курс: учебное пособие – Спб.: Европейский университет, 2001.- С.105-115. Тема 5. Статические игры с неполной информацией (2 занятия) Занятие 1 Вопросы для обсуждения 1. Дуополия Курно с неполной информацией. 2. Условие согласования представлений 3. Семейный спор с малыми случайными параметрами. Практические задания 1. Рассмотрим дуополию Курно для рынка с обратной функцией спроса 2. Рассмотрим дуополию Бертрана с асимметричной информацией и различающейся продукцией. Спрос на продукцию фирмы Затраты будем считать равными нулю для обеих фирм. Чувствительность спроса фирмы
Занятие 2 Вопросы для обсуждения 1. Простой аукцион. 2. Двойной аукцион. 3. Дизайн экономических механизмов. Практические задания 1.Рассмотрите аукцион с закрытыми ставками по первой цене, в котором оценки покупателей независимы и одинаково равномерно распределены на отрезке 2. Рассмотрите аукцион с закрытыми ставками по первой цене, в котором оценки покупателей независимы и одинаково распределены на отрезке 3.Рассмотрим другую интерпретацию двойного аукциона. Пусть имеется фирма и работник, причем фирма знает, какой у нее выигрыш Предположим, что Контрольные вопросы 1. Что называют байесовской игрой? 2. Как определяется равновесие Байеса-Нэша? 3. Что понимается под стратегией игрока в байеской игре? 4. Что такое тип игрока? 5. Что такое пороговые стратегии? 6. Что такое аукцион с закрытыми заявками по первой цене? 7. Как формулируется условие совершенствования сделки в двойном аукционе? 8. Как рассчитывается выигрыши игроков в двойном аукционе? 9. Что называют прямым механизмом? 10. Как формулируется принцип выявления? Задания для самостоятельной работы 1. Изучить, как определяется независимость (некоррелированность) типов в статической игре с неполной информацией. 2. Рассмотреть решение игры «Выбор компьютера» с неполной информацией в симметричном варианте. 3. Изучить игру «Вахтер» как статическую с неполной информацией. 4. Игра «Выбор Компьютера» в несимметричном варианте. Рекомендуемая литература 1. Данилов В.И.Лекции по теории игр: учеб. пособие / - М.: РЭШ, 2002.- С. 98-103. 2. Меньшиков И.С. Лекции по теории игр и экономическому моделированию. – М.: МЗ Пресс, 2007.- С. 121-128, 131-141. 3. Печерский С.Л., Беляева А.А. Теория игр для экономистов. Вводный курс: учебное пособие – Спб.: Европейский университет, 2001.- С. 121-136.
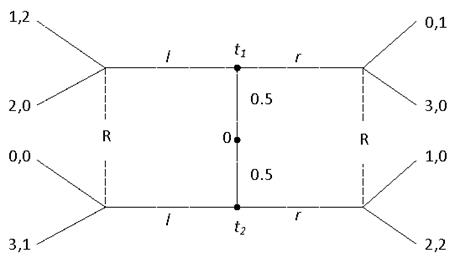
Тема 6. Сигнальные игры (1 занятие) Вопросы для обсуждения 1. Бинарная сигнальная игра. 2. Совершенное байесовское равновесие. 3. Бесплатные сигналы. Бинарная игра с бесплатными сигналами. 4. Непрерывная игра с бесплатными сигналами. Практические задания 1. Найти скрывающее совершенное байесовское равновесие, в котором отправитель любого типа играет r в следующей сигнальной игре:
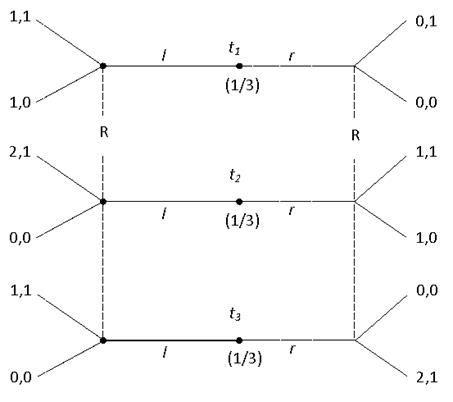
2. Рассмотрим сигнальную игру с тремя типами:
Найти все скрывающие совершенные байесовские равновесия, в которых отправитель любого типа играет l. Контрольные вопросы 1. Что такое сигнал с точки зрения теории игр? 2. Из каких этапов состоит динамический сценарий сигнальной игры с двумя участниками? 3. Как графически изображается бинарная сигнальная игра? 4. Как формулируется алгоритм поиска совершенного байесовского равновесия в бинарной сигнальной игре? 5. Что такое выявляющие и скрывающие стратегии? 6. Что такое скрывающее равновесие? Задания для самостоятельной работы 1. Изучить применение сигналов на рынке труда к модели Спенса. 2. Сформулировать и рассмотреть сигнальную игру «Предприниматель и инвестор». 3. Рассмотреть применение сигналов к моделированию денежной политики государства по отношению к корпорациям. Рекомендуемая литература 1. Акимов В.П. Основы теории игр: учеб. пособие / - М.: МГИМО – Университет, 2008.- С.154-162. 2. Печерский С.Л., Беляева А.А. Теория игр для экономистов. Вводный курс: учебное пособие – Спб.: Европейский университет., 2001.- С.139-167. Раздел 2. Самостоятельная работа Вариант задания следует выбирать как остаток от целого деления на 30 суммы номеров букв фамилии студента. Номера букв брать из таблицы первого индивидуального задания.
Задание 1. Определить верхнюю и нижнюю цену игры и наличие седловой точки в следующих антагонистических играх:
Задание 2.Графически решить игру:
Задание 3. Свести матричную игру к задаче линейного программирования и решить её симплекс – методом (рекомендуется применение компьютерной программы MS Excel с использованием инструмента «Поиск решения»): 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 имеет самый мягкий член шайки. Пиратам удалось ограбить торговый корабль, и им нужно поделить добычу:
имеет самый мягкий член шайки. Пиратам удалось ограбить торговый корабль, и им нужно поделить добычу: 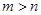 золотых монет. У них принята такая процедура дележа. Первым распределение монет предлагает пират с самым высоким рангом. Если хотя бы половина пиратов (считая предлагающего дележ) согласна с этим предложением, то на этом игра и кончается. Однако, если большинство против выдвинутого предложения, то, следуя своей традиции, они заставляют предлагавшего идти по краю борта с завязанными глазами, пока несчастный не упадет в воду. После этого процедура повторяется. Пираты хотят остаться в живых, но жадны и мстительны: они ценят свою жизнь выше любого количества монет, но если и то, и другое обеспечено, то они хотят увидеть как можно больше своих собратьев, идущих по краю борта с завязанными глазами.
золотых монет. У них принята такая процедура дележа. Первым распределение монет предлагает пират с самым высоким рангом. Если хотя бы половина пиратов (считая предлагающего дележ) согласна с этим предложением, то на этом игра и кончается. Однако, если большинство против выдвинутого предложения, то, следуя своей традиции, они заставляют предлагавшего идти по краю борта с завязанными глазами, пока несчастный не упадет в воду. После этого процедура повторяется. Пираты хотят остаться в живых, но жадны и мстительны: они ценят свою жизнь выше любого количества монет, но если и то, и другое обеспечено, то они хотят увидеть как можно больше своих собратьев, идущих по краю борта с завязанными глазами. для игрока 1 и
для игрока 1 и  – для игрока 2. Докажите на основе обратной индукции, что игрок 1 предлагает в первом периоде решение
– для игрока 2. Докажите на основе обратной индукции, что игрок 1 предлагает в первом периоде решение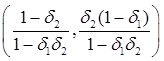
 , где
, где  и
и  – объем выпуска фирмы
– объем выпуска фирмы  . У каждой фирмы предельные затраты c постоянны и нет фиксированных затрат. Фирмы выбирают объем своего выпуска следующим образом: фирма 1 выбирает
. У каждой фирмы предельные затраты c постоянны и нет фиксированных затрат. Фирмы выбирают объем своего выпуска следующим образом: фирма 1 выбирает 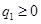 ; фирмы 2 и 3, узнав
; фирмы 2 и 3, узнав  , выбирают одновременно
, выбирают одновременно 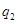 и
и 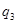 , соответственно. Каково будет совершенное по подыграм равновесие Нэша?
, соответственно. Каково будет совершенное по подыграм равновесие Нэша? на первом шаге. Если исход первого шага –
на первом шаге. Если исход первого шага –  , то играем
, то играем  на втором шаге. Если исход первого шага –
на втором шаге. Если исход первого шага – 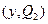 , причем
, причем  , то играем
, то играем  на втором шаге. Если исход первого шага –
на втором шаге. Если исход первого шага – 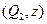 , причем
, причем  , то выберите
, то выберите  на втором шаге. Если решение на первом шаге –
на втором шаге. Если решение на первом шаге –  , причем
, причем  , если
, если  , 0, если
, 0, если  и
и  , если
, если  ; предельные затраты равны
; предельные затраты равны  . Рассмотрим бесконечно повторяющуюся игру, основанную на этой одношаговой игре. Покажите, что фирмы могут использовать релейные стратегии (переключающая при любом отклонении на равновесие Нэша в одношаговой игре), чтобы поддерживать уровень монопольной цены в совершенном по подыграм равновесии Нэша, тогда и только тогда, когда
. Рассмотрим бесконечно повторяющуюся игру, основанную на этой одношаговой игре. Покажите, что фирмы могут использовать релейные стратегии (переключающая при любом отклонении на равновесие Нэша в одношаговой игре), чтобы поддерживать уровень монопольной цены в совершенном по подыграм равновесии Нэша, тогда и только тогда, когда 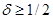 .
. с вероятностью
с вероятностью  и
и  с вероятностью
с вероятностью  ; уровни спроса в разные периоды независимы. Предположим, что в каждом периоде уровень спроса становится известным фирмам до того, как они назначат цены для этого периода. Какие уровни монопольных цен (
; уровни спроса в разные периоды независимы. Предположим, что в каждом периоде уровень спроса становится известным фирмам до того, как они назначат цены для этого периода. Какие уровни монопольных цен (  и
и  ) соответствуют двум уровням спроса? Найдите наименьшее значение
) соответствуют двум уровням спроса? Найдите наименьшее значение  , для которого обе фирмы могут использовать релейные стратегии, чтобы поддерживать уровень монопольной цены (т.е. выбирать
, для которого обе фирмы могут использовать релейные стратегии, чтобы поддерживать уровень монопольной цены (т.е. выбирать  , когда спрос равен
, когда спрос равен  для
для  )в совершенном по подыграм равновесии Нэша. Для каждого значения d между 1/2 и
)в совершенном по подыграм равновесии Нэша. Для каждого значения d между 1/2 и  , чтов совершенном по подыграм равновесии Нэша фирмы могут использовать релейные стратегии, чтобы поддерживать цену
, чтов совершенном по подыграм равновесии Нэша фирмы могут использовать релейные стратегии, чтобы поддерживать цену  , где
, где  –общий спрос на рынке. Обе фирмы имеют одинаковые функции затрат
–общий спрос на рынке. Обе фирмы имеют одинаковые функции затрат  ,но спрос является неопределенным: высоким (
,но спрос является неопределенным: высоким (  )с вероятностью
)с вероятностью  или низким (
или низким (  )с вероятность
)с вероятность 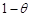 .Информация асимметрична: фирма 1 знает, какой спрос (высокий или низкий), а вторая фирма – нет. Все описание ситуации общеизвестно. Обе фирмы выбирают размер выпуска одновременно. Каково множество стратегий для каждой фирмы? Предположите, что параметры
.Информация асимметрична: фирма 1 знает, какой спрос (высокий или низкий), а вторая фирма – нет. Все описание ситуации общеизвестно. Обе фирмы выбирают размер выпуска одновременно. Каково множество стратегий для каждой фирмы? Предположите, что параметры  и
и  таковы, что равновесные выпуски положительны. Найдите равновесие Байеса-Нэша в этой игре.
таковы, что равновесные выпуски положительны. Найдите равновесие Байеса-Нэша в этой игре. .
. может быть высокой или низкой. Точнее, для каждой фирмы величина
может быть высокой или низкой. Точнее, для каждой фирмы величина 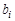 может принимать значение
может принимать значение  с вероятностью
с вероятностью 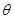 и
и 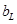 – с вероятностью
– с вероятностью 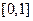 .Покажите, что если число покупателей равно
.Покажите, что если число покупателей равно  , то заявки по цене
, то заявки по цене 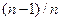 от индивидуальной оценки стоимости составляют равновесие Байеса-Нэша для этого аукциона.
от индивидуальной оценки стоимости составляют равновесие Байеса-Нэша для этого аукциона. .Найдите симметричное равновесие Байеса-Нэша для случая двух участников.
.Найдите симметричное равновесие Байеса-Нэша для случая двух участников. от деятельности работника на данной позиции, а рабочий знает свои альтернативные возможности
от деятельности работника на данной позиции, а рабочий знает свои альтернативные возможности  .Сделка означает, что работник принимается на работу, а цена сделки равна его зарплате
.Сделка означает, что работник принимается на работу, а цена сделки равна его зарплате  .Если сделка заключена, то фирма выигрывает
.Если сделка заключена, то фирма выигрывает  ,а работник выигрывает
,а работник выигрывает