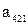|
|
Построение последовательных итераций.Правило работы по методу потенциалов сводится к следующему: 1) находим потенциалы Uk Vl всех поставщиков Аk и потребителей Вl. 2) выбираем какую-нибудь свободную переменную xpq , для которой сумма потенциалов Up + Vq строго больше соответствующей стоимости перевозки (тарифа), это соответствует элементу с отрицательным коэффициентом при этой свободной переменной xpq в правой части выражения функции F. 3) для выбранной в пункте 2 переменной, находим цикл пересчета и производим сдвиг по этому циклу, этот сдвиг приводит к новому допустимому решению. 4) вышеуказанные операции 1-3 повторяются до тех пор, пока не придем к оптимальному базису, т.е. к неотрицательности коэффициентов при свободных переменных в правой части линейной функции F. Получив исходное опорное решение, перейдем к построению новых опорных решений, улучшающих друг друга, применив метод потенциалов. Итак, после построения опорного решения, все переменные разбиты на 2 группы: х kl - базисные переменные х pq - свободные переменные Базисными называются переменные соответствующие занятым клеткам в распределительной таблице. Занятыми клетки становятся в результате занесения в них перевозок по методу северо-западного угла, или методу минимального элемента. Занятых клеток, а, следовательно, базисных переменных всегда должно быть ровно m+n – 1 (m-число строк, а n – число столбцов в таблице). Остальные переменные, соответствующие незанятым клеткам в таблице называются свободными. Используя уравнения (12) и (13) базисные переменные xkl можно выразить через свободные xpq и подставить из в целевую функцию (14). В результате получим выражение F = Для нахождения коэффициентов Uk + Vl = ckl , (16) где ckl - стоимость перевозки единицы груза из пункта Аk в пункт назначения Вl. Доказывается, что совокупность уравнений (16) составленных для всех базисных переменных, образует совместную систему уравнений, причем, значение одной из переменных можно задавать произвольно (обычно задают U1 = 0), и тогда значения остальных переменных находятся из системы однозначно. Обозначим для свободных переменных сумму соответствующих потенциалов через С′ pq , т.е. Up + Vq = С¢ pq и назовем косвенной стоимостью (в отличие от данной стоимости, т.е.тарифа сpq), тогда доказывается, что коэффициенты при свободных переменных в равенстве (15) имеют вид:
Если все величины Воспользуемся изложенными общими понятиями и продолжим решение примеров. Продолжение примера 9. Мы получили исходное опорное решение, следуя методу минимального элемента в виде X1 = Для нахождения потенциалов необходимо использовать систему:
U1 + V2 = c12 = 10 U1 + V3 = c13 = 4 U2 + V2 = c22 = 2 Значение одной из неизвестных зададим произвольно, например U1 = 0, а остальные найдем из системы: V1 = 6, V2 = 10, V3 = 4, U2 = -8 Далее вычисляем косвенные стоимости: С¢21 = U2 + V1 = -8 + 6 = -2 С¢23 = U2 + V3 = -8 + 4 = -4 Подсчитаем теперь разности
тогда F = 1020 + 14 х21 + 12 х23 Среди коэффициентов при переменных в правой части нет отрицательных, следовательно, исходное опорное решение является оптимальным. Таким образом, правило минимального элемента сразу дало оптимальное решение. Продолжение примера 8. Первоначальное опорное решение согласно правилу северо-западного угла имеет вид: X = Для нахождения потенциалов, необходимо решить систему:
U1 + V2 = c12 = 10 U2 + V2 = c22 = 2 U2 + V3 = c23 = 8 Значение одной из неизвестных зададим произвольно, например U1 = 0, а остальные найдем из системы: V1 = 6, V2 = 10, U2 = -8, V3 = 16. Вычисляем косвенные стоимости: С¢13 = U1 + V3 = 0 + 16 = 16 С¢21 = U2 + V1 = -8 + 6 = -2 Затем посчитаем разности
следовательно F= 1860 - 12 х13 + 14 х21 Среди коэффициентов при переменных в правой части есть отрицательный (при х13 ), следовательно, можно попытаться уменьшить значение F, увеличив х13 (сохранив нулевое значение х21). Положим х13 = l Поскольку суммы значений неизвестных (перевозок) по строкам и столбцам должны остаться неизменными, то следует произвести следующий балансовый перерасчет: Таблица 6
Добавление l к х22 компенсируется вычитанием l из х12 , а это в свою очередь, прибавлением к х13 , вычитанием из х23 Мы получим так называемый цикл пересчета. После несложных рассуждений можно заключить, что l = 70. Получаем следующее опорное решение X2 = Как можно видеть (по предыдущему решению) оно является оптимальным.
Задача №4 Условие задачи представляют в табличной форме, а полученную матрицу называют платежной (матрицей игры). При решении игровых задач торговли применяют специальные критерии для анализа ситуации, связанной с принятием решений. Такими критериями являются: 1. Критерий Лапласа, который основан на вероятностях состояния природы. Если эти вероятности не известны, то можно предположить, что эти вероятности равны для всех состояний природы, т.е.
Если при этом 2. Максимальный критерий Вальда основан на осторожном поведении лица, принимающего решение, и заключается в выборе наилучшей ситуации из худших, т.е. выбирается максимальное число из всех выбранных ранее минимальных:
3. Критерий Гурвица охватывает ряд различных подходов к принятию решений от наиболее оптимистического до консервативного, т.е. вместо двух крайностей придерживаться некоторого промежуточного решения. Тогда решению, принятому по критерию Гурвица соответствует:
4. Критерий минимаксного риска Сэвиджа позволяет путем замены платежной матрицы матрицей потерь (риска) определить оптимальную стратегию:
где
Пример 9. Розничное торговое предприятие разработало несколько вариантов плана продажи товаров на предстоящей ярмарке с учетом меняющейся конъюнктуры рынка и спроса покупателей, получающиеся от их возможных сочетаний величины прибыли представлены в виде матрицы выигрышей. Определить оптимальный план продажи товаров.
X=0,6 Таблица 2
1. По критерию Вальда (Таблица №8) мы должны найти 2. Применим критерий Лапласа.
Итак, имеем: Подставив значения из таблицы №7, имеем, что оптимальной стратегией является П2. 3. Применим критерий Гурвица. Вычислим при Подставляя значения из Таблицы №8 получаем Выберем По критерию Гурвица оптимальной является стратегия П2. 4. Построим матрицу риска Сэвиджа по формуле: Таблица 9
Риск необходимо свести к минимуму, т.е. в последнем столбце Таблицы №9 выбираем наименьшее значение Т.к. по 2-м предыдущим критериям выбрали П2, то и здесь П2.
ВОПРОСЫ К ЭКЗАМЕНУ По дисциплине «Методы оптимальных решений» за 1 семестр для заочного отделения по направлению подготовки «Экономика», профилям «Бухгалтерский учет, анализ и аудит», «Финансы и кредит».
1. Системы линейных неравенств. Множество решений системы линейных неравенств. 2. Основная задача линейного программирования. Целевая функция. Макси- мизация и минимизация целевой функции. Ограничения. 3. Общий вид математической постановки задачи линейного программиро- вания. 4. Основная и каноническая формы записи ЗЛП, их взаимосвязь. 5. Графический метод решения ЗЛП. Область допустимых решений. 6. Симплекс-метод. Базисные и свободные переменные. Симплекс-таблица. Построение симплекс-таблицы. 7. Геометрическая интерпретация симплексного метода. Теорема об опорном решении и угловой точке. 8. Достаточные условия существования оптимального решения ЗЛП, признак оптимальности опорного решения. 9. Алгоритм симплекс-метода. 10. Двойственность в линейном программировании, Построение симметрич- ной двойственной задачи. 11. Связь оптимальных решений пары двойственных задач. 12. Теоремы двойственности. 13. Определение двойственных переменных симметричной ЗЛП симплекс- ным методом. 14. Определение двойственных оценок ЗЛП. Экономическая интерпретация двойственных оценок. 15. Транспортная задача. Открытая и закрытая модели. 16. Определение исходного опорного решения по правилу «северо-западного угла». 17. Определение исходного опорного решения по правилу «минимальной стоимости». 18. Построение нового опорного решения с помощью метода потенциалов. 19. Оптимальное решение ТЗ методом потенциалов. Признак оптимальности. 20. Расчет потенциалов и оценок свободных клеток. 21. Понятие цикла. Правило пересчета решения по циклу. 22. Критерий Лапласа. 23. Критерий Гурвица. 24. Критерий Сэвиджа. 25. Критерий Вальда. 26. Роль и место моделирования в исследовании систем. 27. Предмет теории моделирования. 28. Классификация моделей. Оформление контрольной работы Результатом допуска к зачету по дисциплине «Методы оптимальных решений» является решенная контрольная работа со всеми заданиями с отметкой преподавателя «Зачтено». Если решенная работа не зачтена, студенту необходимо устранить замечания и сдать контрольную на повторное рецензирование. Контрольная работа по" методам оптимальных решений" выполняется в тетради, на титульном листе контрольной необходимо написать название дисциплины, наименование факультета (специальность), курс, фамилию, имя и отчество студента. Перед решением каждой задачи полностью записать ее условие. Решение задач сопровождается развернутыми расчетами и краткими пояснениями. Записать ответ. В конце контрольной работы привести список цитируемой литературы, дату и подпись. После получения отрецензированной работы студент должен сделать работу над ошибками. Контрольная работа, выполненная не в соответствии с данными условиями задач, или оформленная на ПК не рецензируется и не зачитывается.
Список использованных источников
1. Интрилигатор М. Математические методы оптимизации и экономическая теория. М.: Изд. Айрис-Пресс, 2002. (гл. 5) 2. Вентцель Е.С. Исследование операций. Задачи, принципы, методология. М.: Высшая школа, 2001. (гл. 3) 3. Фомин Г.П.Математические методы и модели в коммерческой деятельности. М.: «Финансы и статистика», 2010. 4. Глухов В.В., Медников М.Д., Коробко С.Б. Математические методы и модели для менеджмента. СПб.: Лань, 2000. (гл. 8, 9). 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 pq х pq +
pq х pq +  F = 1020
F = 1020 U1 + V1 = c11 = 6
U1 + V1 = c11 = 6
 F = 1860
F = 1860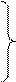 U1 + V1 = c11 = 6
U1 + V1 = c11 = 6
 90 - l
90 - l
 l
l
 20 + l
20 + l
 .
.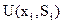 представляет получаемый выигрыш (например, прибыль), то получим решение такое, которое обеспечивает
представляет получаемый выигрыш (например, прибыль), то получим решение такое, которое обеспечивает  .
.
 , где a – показатель оптимизма, величина которого может принимать значения:
, где a – показатель оптимизма, величина которого может принимать значения:  .
. ,
, - элементы матрицы риска,
- элементы матрицы риска, - элементы платежной матрицы
- элементы платежной матрицы -максимальный элемент в k- ом столбце платежной матрицы.
-максимальный элемент в k- ом столбце платежной матрицы. Таблица 7
Таблица 7
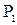



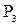





 , т.е.
, т.е. 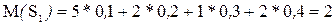 .
. .
. для четырех стратегий.
для четырех стратегий. .
.