
|
|
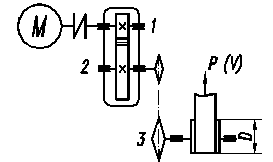
Примеры расчета зубчатых передач12 Пример 1.Рассчитать цилиндрическую прямозубую передачу привода ленточного транспортера. Схема привода
Исходные данные. Усилие на ленте транспортера P=8 кН. Скорость ленты транспортера V=2 м/с. Диаметр барабана D=400 мм. Передаточное число цепной передачи uц=2.5. Срок службы передачи L = 5 лет. Коэффициент использования передачи: в течение года Kг =0.9 в течение суток Kс =0.6. Продолжительность включения ПВ%=25%. Режим работы легкий. Тип привода нереверсивный. Цепная передача закрытая.
1. Выбор электродвигателя и расчет основных параметров привода. 1.1. Выбор электродвигателя Требуемая мощность электродвигателя Pтр= где
здесь Тогда Pтр= По требуемой мощности из табл.11 выбираем асинхронный электродвигатель 4А180М6 с ближайшей большей стандартной мощностью Pэ=18.5 кВт, синхронной частотой вращения nс=1000 об/мин и скольжением S=2.7%.
1.2. Частота вращения вала двигателя n1= nс• (1- 1.3. Требуемая частота вращения барабана nб= 1.4. Общее передаточное число привода uo= 1.5. Передаточное число зубчатой передачи u’= Передаточное число цилиндрической зубчатой передачи редуктора рекомендуется выбирать из диапазона 2.5<u<5. Если это ограничение не выполняется, следует изменить синхронную скорость двигателя и повторить расчет. Если выполняется, то полученное значение u’ округляют до ближайшего стандартного из табл.3. Принимаем u=4. 1.6. Частоты вращения валов (индекс соответствует номеру вала на схеме привода) n1=973 об/мин, n2= n3= 1.7. Мощности, передаваемые валами. P1=Pтр=17.53 кВт, P2=P1 P3=P2 1.8.Крутящие моменты, передаваемые валами. Крутящий момент на валу определяется по формуле Ti=9550 T1=9550 T2=9550 T3=9550
Расчет зубчатой передачи 2.1. Выбор материалов зубчатых колес Определяем размеры характерных сечений заготовок по формулам ( 1 ), принимая, что при передаточном числе зубчатой передачи u > 2.5 шестерня изготавливается в виде вал-шестерни. Тогда Dm1=24• Sm2= 1.2• Диаметр заготовки для колеса равен dк = u•Dm1=4•84.1=336.4 мм. Выбираем для колеса и шестерни сталь 40Х, термообработка улучшение, твердость поверхности зуба шестерни 269…302 НВ, Dm=125 мм > Dm1, твердость поверхности зуба колеса 235…262 НВ, Sm=125 мм > Sm2. Определяем средние значения твердости поверхности зуба шестерни и колеса
НВ1= 0.5•(НВ1min+ НВ1max)= 0.5•(269+302)=285.5, НВ2= 0.5•(НВ2min+ НВ2max)= 0.5•(235+262)=248.5.
2.2. Определение допускаемых напряжений 2.2.1. Допускаемые контактные напряжения
Для определения пределов контактной выносливости используем формулы из табл.5: sHlim1= 2 НВ1 + 70=2•285.5+70=641 МПа, sHlim2= 2 НВ2 + 70=2•248.5+70=567 МПа. Коэффициенты безопасности SH1=1.1, SH2=1.1 (табл.5). Коэффициенты долговечности равны КHLj = Базовые числа циклов при действии контактных напряжений NHO1=23.5•106, NHO2 =16.8•106 (табл.4). Эквивалентные числа циклов напряжений определим по формуле NHE j= где коэффициент эквивалентности для легкого режима работы Суммарное число циклов нагружения равно NSj = 60•nj•c•th , где с=1, суммарное время работы передачи th=L•365•24•KГ•КС•ПВ, здесь ПВ=0.01•ПВ%=0.01•25=0.25. В результате расчетов получим th=5•365•24•0.9•0.6•0.25=5913 ч, NS1 = 60•973•5913=3.45•108, NS2 = 60•243.25•5913=0.863•108, NHE1= 0.125•3.45•108=43.1•106, NHE2= 0.125•0.863•108=10.8•106 . Поскольку NHE1> NHO1, принимаем КHL1=1. КHL2 = Определим допускаемые контактные напряжения для шестерни и колеса
Допускаемые контактные напряжения для прямозубой передачи
2.2.2. Допускаемые напряжения изгиба
Коэффициенты безопасности при изгибе: SF1=1.7, SF2=1.7. Коэффициенты, учитывающие влияние двухстороннего приложения нагрузки, для нереверсивного привода: KFС1=1, KFС2=1. Коэффициенты долговечности, определим по формуле КFLj = где qj - показатель степени кривой усталости q1=6, q2=6 (табл.6), NFO = 4•106 – базовое число циклов при изгибе. Эквивалентное число циклов напряжений при изгибе NFE j= NFE1=0.038•3.45•108=13.11•106, NFE2=0.038•0.863•108=3.278•106
Поскольку NFE1> NFO, принимаем КFL1=1. КFL2 = Определим допускаемые напряжения изгиба для шестерни и колеса:
2.3. Проектный расчет передачи 2.3.1. Межосевое расстояние передачи определим по формуле где Коэффициент ширины зубчатого венца для прямозубых передач принимаем Полученное межосевое расстояние округлим до ближайшего большего стандартного значения (табл.2): 2.3.2. Модуль, числа зубьев колес и коэффициенты смещения Рекомендуемый диапазон для выбора модуля m= Из полученного диапазона выберем стандартный модуль по табл.1: m=2.5 мм. Суммарное число зубьев передачи: Z Число зубьев шестерни: Z1= Число зубьев колеса: Z2= Z Фактическое передаточное число: uф= При u
Учитывая, что Z1> 17, принимем коэффициенты смещения x1=0, x2=0.
2.3.3. Ширина зубчатых венцов и диаметры колес Ширину зубчатого венца колеса определим по формуле: bw2= Округлим bw2 до ближайшего числа из ряда нормальных линейных размеров на с.6: bw2=63 мм. Ширину зубчатого венца шестерни bw1 принимают на 2…5 мм больше чем bw2. Примем bw1=67 мм. Определим диаметры окружностей зубчатых колес: делительные окружности dj=mZj, d1=2.5•32=80 мм, d2=2.5•128=320 мм, окружности вершин зубьев daj = dj+2 m (1+xj), da1 =80+2•2.5=85 мм, da2 =320+2•2.5=325 мм, окружности впадин зубьев dfj = dj-2 m (1.25- xj), df1 =80-2•2.5•1.25=73.75 мм, df2 =320-2•2.5•1.25=313.75 мм.
2.3.4. Окружная скорость в зацеплении и степень точности передачи V= Для полученной скорости назначим степень точности передачи nст=8 (табл.8).
2.4. Проверочный расчет передачи 2.4.1. Проверка контактной прочности зубьев Для проверочного расчета зубьев на контактную прочность используем формулу
где Z Коэффициент контактной нагрузки определим по формуле КН = KHα KHβ КНV, где KHα - коэффициент неравномерности распределения нагрузки между зубьями, KHβ – коэффициент неравномерности распределения нагрузки по ширине колеса, КНV – динамический коэффициент. Коэффициент KHα найдем по формуле: KHα =1+A•(nст-5)•К где А=0.06 для прямозубых передач, К К Тогда KHα =1+0.06•(8-5)•0.32=1.058. Коэффициент KHβ определим по формуле: KHβ = 1+ (K где K
По значению KHβ = 1+ (1.03-1) •0.32=1.01, Коэффициент КНV=1.196 определим методом интерполяции по табл.10. Окончательно найдем КН и КН = 1.058•1.01•1.196=1.278.
Поскольку
2.4.2. Проверка изгибной прочности зубьев Для определения напряжения изгиба в зубе шестерни используем формулу:
Коэффициент формы зуба при xj=0 равен YFj=3.47+ YF1=3.47+ Коэффициент нагрузки при изгибе найдем по формуле: KF = KFα KFβ KFV. Для определения составляющих коэффициентов используем следующие зависимости: KFα =1 для прямозубых передач, KFβ = 0.18+0.82 K KFβ = 0.18+0.82•1.03=1.025, KFV = 1+1.5•(1.196-1)=1.294, KF =1•1.025•1.294=1.326. Тогда Напряжение изгиба в зубьях колеса равно:
2.5. Силы в зубчатой передаче Окружная сила Ft= Распорная сила Fr= Ft•tg2
Пример 2.Рассчитать цилиндрическую косозубую передачу привода ленточного транспортера. Исходные данные взять из примера 1. 1. Выбор электродвигателя и расчет основных параметров привода. См. пример 1. Расчет зубчатой передачи 2.1. Выбор материалов зубчатых колес Определяем размеры характерных сечений заготовок по формулам ( 1 ), принимая, что при передаточном числе зубчатой передачи u > 2.5 шестерня изготавливается в виде вал-шестерни. Тогда Dm1=20• Sm2= 1.2• Диаметр заготовки для колеса равен dк = u•Dm1=4•70.1=286.4 мм. Выбираем для шестерни сталь 40ХН, термообработка улучшение с последующей закалкой ТВЧ, твердость поверхности зуба шестерни 48…53 НRC, Dm=200 мм > Dm1, Выбираем для колеса сталь 45, термообработка улучшение, твердость поверхности зуба колеса 235…262 НВ, Sm=80 мм > Sm2. Определяем средние значения твердости поверхности зуба шестерни и колеса НRC1= 0.5•(НRC1min+ НRC1max)= 0.5•(48+53)=50.5, НВ2= 0.5•(НВ2min+ НВ2max)= 0.5•(235+262)=248.5.
2.2. Определение допускаемых напряжений 2.2.1. Допускаемые контактные напряжения
Для определения пределов контактной выносливости используем формулы из табл.5: sHlim1= 17 HRC1 + 200==17•50.5+200=1058.5 МПа. sHlim2= 2 НВ2 + 70=2•248.5+70=567 МПа. Коэффициенты безопасности SH1=1.2, SH2=1.1 (табл.5). Коэффициенты долговечности равны КHLj = Базовые числа циклов при действии контактных напряжений NHO1=86.9•106, NHO2 =16.8•106 (табл.4). Эквивалентные числа циклов напряжений определим по формуле NHE j= где коэффициент эквивалентности для легкого режима работы Суммарное число циклов нагружения равно NSj = 60•nj•c•th , где с=1, суммарное время работы передачи th=L•365•24•KГ•КС•ПВ, здесь ПВ=0.01•ПВ%=0.01•25=0.25. В результате расчетов получим th=5•365•24•0.9•0.6•0.25=5913 ч, NS1 = 60•973•5913=3.45•108, NS2 = 60•243.25•5913=0.863•108, NHE1= 0.125•3.45•108=43.1•106, NHE2= 0.125•0.863•108=10.8•106 . Вычислим коэффициенты долговечности
КHL1 =
Определим допускаемые контактные напряжения для шестерни и колеса
Допускаемые контактные напряжения для косозубой передачи sHP=0.45 (sHP1+sHP2) sHP=0.45 (991.46+554.8)=695.81 МПа, s Учитывая, что sНР>1.23•sHP2, окончательно принимаем sHP=682.4 МПа.
2.2.2. Допускаемые напряжения изгиба
Коэффициенты безопасности при изгибе: SF1=1.7, SF2=1.7. Коэффициенты, учитывающие влияние двухстороннего приложения нагрузки для нереверсивного привода: KFС1=1, KFС2=1. Коэффициенты долговечности, определим по формуле КFLj = где qj - показатель степени кривой усталости q1=9, q2=6 (табл.6), NFO = 4•106 – базовое число циклов при изгибе. Эквивалентное число циклов напряжений при изгибе NFE j= NFE1=0.016•3.45•108=5.52•106, NFE2=0.038•0.863•108=3.278•106
Поскольку NFE1> NFO, принимаем КFL1=1. КFL2 = Определим допускаемые напряжения изгиба для шестерни и колеса:
2.3. Проектный расчет передачи 2.3.1. Межосевое расстояние передачи определим по формуле где Коэффициент ширины зубчатого венца для косозубых передач принимаем Полученное межосевое расстояние округлим до ближайшего большего стандартного значения (табл.2): 2.3.2. Модуль, числа зубьев колес и коэффициенты смещения Рекомендуемый диапазон для выбора модуля mn= mn=(0.01…0.02)•140=1.4…2.8 мм. Из полученного диапазона выберем стандартный модуль mn=2 мм по табл.1, учитывая, что для силовых передач модуль меньше 2 мм применять не рекомендуется. Суммарное число зубьев передачи: Z Полученное значение Z
Число зубьев шестерни: Z1= Округлим полученное значение до ближайшего целого числа Z1=27. Число зубьев колеса: Z2= Z Фактическое передаточное число: uф= При u
Если Z1> 17, то принимают коэффициенты смещения x1=0, x2=0.
2.3.3. Ширина зубчатых венцов и диаметры колес Ширину зубчатого венца колеса определим по формуле bw2= Округлим bw2 до ближайшего числа из ряда нормальных линейных размеров на с.6: bw2=56 мм. Ширину зубчатого венца шестерни bw1 принимают на 2…5 мм больше чем bw2. Примем bw1=60 мм. Определим диаметры окружностей зубчатых колес: делительные окружности dj= d1= окружности вершин зубьев daj = dj+2 m (1+xj), da1 =55.182+2•2=59.182 мм, da2 =224.817+2•2=228.817 мм, окружности впадин зубьев dfj = dj-2 m (1.25- xj), df1 =55.182-2•2•1.25=50.182 мм, df2 =224.817-2•2•1.25=219.817 мм, 2.3.4. Окружная скорость в зацеплении и степень точности передачи V= Для полученной скорости назначим степень точности передачи nст=8 (табл.8), учитывая, что nст=9 для закрытых зубчатых передач применять не рекомендуется.
2.4. Проверочный расчет передачи 2.4.1. Проверка контактной прочности зубьев Для проверочного расчета зубьев на контактную прочность используем формулу
где Z Коэффициент контактной нагрузки определим по формуле КН = KHα KHβ КНV, где KHα - коэффициент неравномерности распределения нагрузки между зубьями, KHβ – коэффициент неравномерности распределения нагрузки по ширине колеса, КНV – динамический коэффициент. Коэффициент KHα найдем по формуле: KHα =1+A•(nст-5)•К где А=0.15 для косозубых передач, К К Тогда KHα =1+0.15•(8-5)•0.274=1.123. Коэффициент KHβ определим по формуле: KHβ = 1+ (K где K
По значению KHβ = 1+ (1.04-1) •0.274=1.011, Коэффициент КНV=1.056 определим методом интерполяции по табл.10. Окончательно найдем КН и КН = 1.123•1.011•1.056=1.199,
Поскольку
2.4.2. Проверка изгибной прочности зубьев Для определения напряжения изгиба в зубе шестерни используем формулу:
Коэффициент формы зуба при xj=0 равен: YFj=3.47+ ZV1=
YF1=3.47+ Коэффициент, учитывающий влияние угла наклона зуба на его прочность, KF = KFα KFβ KFV. Для определения составляющих коэффициентов используем следующие зависимости: KFα =1+0.15•(nст-5), KFβ = 0.18+0.82 K В результате получим KFα =1+0.15•(nст-5)=1+0.15• (8-5)=1.45, KFβ = 0.18+0.82•1.04=1.033, KFV = 1+1.5•(1.056-1)=1.084, KF =1.45•1.033•1.084=1.62. Тогда Напряжение изгиба в зубьях колеса равно:
2.5. Силы в зубчатой передаче Окружная сила Ft= Распорная сила Fr= Ft• Осевая сила Fа= Ft•tg
Список литературы 1. Дунаев П.Ф., Леликов О.П. Конструирование узлов и деталей машин. М.: Издательский центр “Академия”, 2003. 496 с. 2. Куклин Н.Г., Куклина Г.С., Житков В.К. Детали машин. М.: Илекса, 1999. 392 с. 3. Иосилевич Г.Б. Детали машин М.: Машиностроение, 1988. 367 с.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
,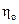 - общий коэффициент полезного действия привода:
- общий коэффициент полезного действия привода:

 =0.98•0.96•0.993=0.913,
=0.98•0.96•0.993=0.913,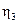 - КПД одной пары подшипников качения, согласно табл.12 примем
- КПД одной пары подшипников качения, согласно табл.12 примем  =17.53 кВт.
=17.53 кВт. )=1000 • (1-
)=1000 • (1-  )=973 об/мин.
)=973 об/мин. =
=  =95.49 об/мин.
=95.49 об/мин. =
=  =10.18.
=10.18. =
=  =4.072.
=4.072. =
=  =243.25 об/мин,
=243.25 об/мин, =
=  =97.3 об/мин.
=97.3 об/мин. =17.53•0.98•0.99 =17.008 кВт,
=17.53•0.98•0.99 =17.008 кВт, =17.008•0.96•0.99=16.164 кВт.
=17.008•0.96•0.99=16.164 кВт. . Тогда
. Тогда =172.05 Н•м,
=172.05 Н•м,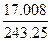 =667.73 Н•м,
=667.73 Н•м, =1586.49 Н•м.
=1586.49 Н•м. = 24•
= 24•  =84.1 мм,
=84.1 мм,
 •
• 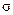 HPj=
HPj=  .
.
 1.
1. h•NΣj, ,
h•NΣj, , =1.077.
=1.077. =582.73 МПа,
=582.73 МПа,  =555.15 МПа, sHPj min=
=555.15 МПа, sHPj min=  HP2.
HP2.
 .
.
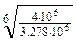 =1.034.
=1.034. =
=  =293.89 МПа,
=293.89 МПа, 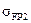 =
=  =264.51 МПа.
=264.51 МПа. =
= 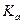 •(u + 1)
•(u + 1)  ,
, =0.315 (ряд на с.1). На этапе проектного расчета задаемся значением коэффициента контактной нагрузки КН=1.2. Тогда
=0.315 (ряд на с.1). На этапе проектного расчета задаемся значением коэффициента контактной нагрузки КН=1.2. Тогда =182.28 мм.
=182.28 мм. =(0.01…0.02)•200=2…4 мм.
=(0.01…0.02)•200=2…4 мм. =
= 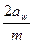 =
=  =160.
=160. =
=  =32.
=32. =
=  =4.
=4. 4.5 отличие фактического передаточного числа от номинального должно быть не больше 2.5%.
4.5 отличие фактического передаточного числа от номинального должно быть не больше 2.5%. u=100
u=100  =100
=100  =0.
=0. =
=  =4.076 м/с.
=4.076 м/с. =
= 

 ,
, = 9600 для прямозубых передач.
= 9600 для прямозубых передач.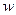 ,
, -1) К
-1) К  :
:
 =501.3 МПа.
=501.3 МПа. =100
=100  =9.7%<15%.
=9.7%<15%. .
. , ZV1=32, ZV2=128,
, ZV1=32, ZV2=128, =3.883, YF2=3.47+
=3.883, YF2=3.47+  =3.573.
=3.573. =3.883
=3.883  =132.2 МПа <
=132.2 МПа <  .
.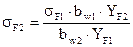 =
=  =129.4 МПа <
=129.4 МПа <  .
. =
=  =4301.3 Н.
=4301.3 Н. =4301.3•0.364=1565.5 Н.
=4301.3•0.364=1565.5 Н. =1.124, КHL2 =
=1.124, КHL2 =  =991.46 МПа,
=991.46 МПа, 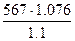 =554.8 МПа, sHPj min=
=554.8 МПа, sHPj min=  =1.23•sHPj min=682.4 МПа.
=1.23•sHPj min=682.4 МПа. =352.9 МПа,
=352.9 МПа,  =
= 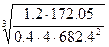 =133.65 мм.
=133.65 мм. =
=  =
= 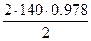 =136.94,
=136.94, = arccos
= arccos  =arccos
=arccos 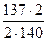 =
=  .
. =
=  =27.4.
=27.4.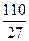 =4.074.
=4.074. =100
=100  =1.85%<2.5%.
=1.85%<2.5%. ,
, =55.182 мм, d2=
=55.182 мм, d2=  =224.817 мм,
=224.817 мм, =2.811 м/с.
=2.811 м/с. ,
, :
: :
:
 =652.09 МПа.
=652.09 МПа.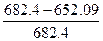 =4.44%<15%.
=4.44%<15%. .
. - эквивалентное число зубьев:
- эквивалентное число зубьев: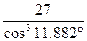 =28.81, ZV2=
=28.81, ZV2=  =117.38,
=117.38, =3.93, YF2=3.47+
=3.93, YF2=3.47+  =3.58.
=3.58. для косозубых передач. Коэффициент нагрузки при изгибе определим по формуле:
для косозубых передач. Коэффициент нагрузки при изгибе определим по формуле: =172.03 МПа <
=172.03 МПа <  =167.9 МПа <
=167.9 МПа <  =6236 Н.
=6236 Н. =6236•
=6236• 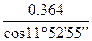 =2319 Н.
=2319 Н. =6236•tg
=6236•tg