
|
|
Расчет зубчатых цилиндрических передач12 Федеральное агентство по образованию ГОУ ВПО “Уральский государственный технический университет – УПИ”
Расчет зубчатых цилиндрических передач
Методические указания по курсам “Детали машин и основы конструирования” и “Прикладная механика” для студентов технических специальностей всех форм обучения (электронная версия)
Составитель профессор, доктор техн. наук Г.Л.Баранов. Научный редактор доц., канд. техн. наук Ю.В.Песин
Введение Цилиндрические зубчатые передачи находят широкое применение в современном машиностроении. Методика прочностного расчета для цилиндрических зубчатых передач внешнего зацепления с эвольвентным профилем зуба регламентирована ГОСТ 21354-87. В соответствии с этим ГОСТом основными видами расчета на прочность таких передач являются: расчет на контактную выносливость для предотвращения усталостного выкрашивания активных поверхностей зубьев и расчет на выносливость при изгибе для предотвращения усталостного излома зуба. Расчет на контактную выносливость позволяет определить межосевое расстояние зубчатой передачи, а расчет на выносливость при изгибе позволяет определить модуль. Основными параметрами цилиндрической зубчатой передачи являются: модуль, передаточное число, межосевое расстояние и коэффициент ширины зубчатого венца. Модуль m выбирается по табл.1.
Таблица 1. Модули по ГОСТ 9563-60
Межосевое расстояние awвыбирается по табл.2.
Таблица 2
Межосевые расстояния по ГОСТ 2185-66
Передаточное число uвыбирается по табл.3
Таблица 3.
Передаточные числа по ГОСТ 2185-66.
Коэффициент ширины зубчатого венца yba выбирается из стандартного ряда: 0.16 0.25 0.315 0.4 0.5 0.63 0.8 1.0 по ГОСТ 2185-66. При выборе основных параметров первый ряд следует предпочитать второму.
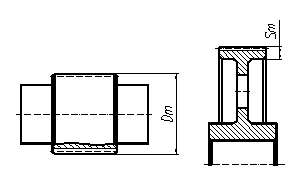
1. Выбор материалов зубчатых колес и способов термообработки Наибольшее применение в редукторах находят стальные зубчатые колеса. Механические характеристики сталей, рекомендуемых для изготовления зубчатых колес, приведены в табл.4. В таблице приняты следующие обозначения: способы термообработки Н – нормализация, У – улучшение, З – закалка, Ц - цементация; Dm - наружный диаметр заготовки вал-шестерни, Sm – характерный размер заготовки для насадного зубчатого колеса (рис.1). Таблица 4 Механические характеристики сталей
. Рис.1. Характерные размеры сечения заготовки Для ориентировочного определения Dm и Sm используются следующие формулы: Dm=(20…24) где T1 – крутящий момент на шестерне в Н•м, u – передаточное число зубчатой передачи. Коэффициент 20 в формуле для Dm используется при расчете косозубых и шевронных передач, для прямозубых передач принимается коэффициент 24. Величина Dm определяется при проектировании вал-шестерни, Sm – при проектировании насадных зубчатых колес. Для зубчатых передач рекомендуются следующие варианты материалов и термообработок (ТО): 1- Марки сталей одинаковы для колеса и шестерни 40, 45, 40Х, 40ХН и 35ХМ. Термообработка – улучшение. Твердость зуба шестерни 269…302 НВ, твердость зуба колеса 235…262 НВ. 2- Марки сталей одинаковы для колеса и шестерни 40, 45, 40Х, 40ХН и 35ХМ. Термообработка зуба шестерни– улучшение с последующей закалкой ТВЧ, твердость поверхности зуба шестерни 45…50 НRC, или 48…53 НRC. Термообработка зуба колеса – улучшение, твердость зуба колеса 235…262 НВ. 3- Марки сталей одинаковы для колеса и шестерни 40, 45, 40Х, 40ХН и 35ХМ. Термообработки колеса и шестерни одинаковы – улучшение с последующей закалкой ТВЧ, твердость поверхности зуба шестерни и колеса 45…50 НRC, или 48…53 НRC. 4- Марки сталей для колеса 40Х, 40ХН и 35ХМ. Термообработка колеса – улучшение с последующей закалкой ТВЧ, твердость поверхности зуба колеса 45…50 НRC, или 48…53 НRC. Марки сталей для шестерни 20Х, 20ХНМ и 18ХГТ. Термообработка шестерни – улучшение с последующей цементацией и закалкой, твердость поверхности зуба шестерни 56…63 НRC. Ориентировочно диаметр заготовки зубчатого колеса определяется по формуле dк = u•Dm. Если диаметр заготовки колеса dк > 500 мм, то в качестве материала для колеса рекомендуется использовать стальное литье из сталей марок 35Л и 45Л.
2. Расчет допускаемых напряжений 2.1.Расчет допускаемых контактных напряжений Допускаемые контактные напряжения определяются по формуле
где j=1 для шестерни, j=2 для колеса, sHlim j - предел контактной выносливости, КHLj - коэффициент долговечности, SHj - коэффициент безопасности. Предел контактной выносливости и коэффициент безопасности зависят от способа термической или химико-термической обработки и твердости поверхности зуба. Формулы для определения sHlim, значения SH и KHmax приведены в табл.5. Средняя твердость поверхности зуба равна НВ = 0.5 (НВmin + НВmax) или HRC = 0.5 (HRCmin + HRCmax).
Таблица 5 Данные для расчета допускаемых контактных напряжений
Коэффициент долговечности определяется по формуле КHLj = где NHOj – базовое число циклов при действии контактных напряжений; NHEj – эквивалентное число циклов напряжений. Должно выполняться условие КHLj Значения базового число циклов, рассчитанные по формуле NHO = 30 •HB2.4 NHE j= где
Таблица 6 Характеристики типовых режимов нагружения
При постоянной частоте вращения NΣj определяется по формуле
NSj = 60•nj•c•th , ( 3 )
где nj - частота вращения колеса в об/мин, с – число зацеплений за один оборот колеса, th – суммарное время работы передачи в часах; th = L•365•24•KГ•КС•ПВ; здесь Kг – коэффициент использования передачи в течение года; Kс – коэффициент использования передачи в течение суток; L – срок службы передачи в годах; ПВ – относительная продолжительность включения. Расчет допускаемых контактных напряжений для зубьев шестерни и колеса sHP1 и sHP2 выполняется по формуле ( 2 ). Допускаемые контактные напряжения передачи равны sHP=sHPjmin - для прямозубой передачи, sHP=0.45 (sHP1+sHP2) здесь sHPj min- меньшее из допускаемых контактных напряжений для шестерни и колеса.
2.2.Расчет допускаемых напряжений изгиба
Допускаемые напряжения изгиба определяются по формуле
где sF lim j - предел изгибной выносливости зубьев, SFj - коэффициент безопасности, KFСj - коэффициент, учитывающий влияние двухстороннего приложения нагрузки, KFLj - коэффициент долговечности, определяемый по формуле: КFLj = здесь qj - показатель степени кривой усталости (табл.6), NFO = Должно выполняться условие КFLj Формулы для определения sF lim и значения SF, KFLmax и KFС для реверсивного привода приведены в табл.7. Для нереверсивного привода KFС=1. Эквивалентное число циклов напряжений при изгибе равно: NFE j= где NΣj определяется по формуле ( 3 ), (табл. 6).
Таблица 7
Данные для расчета допускаемых напряжений изгиба
3.Проектный расчет передачи Межосевое расстояние передачи определяют из расчета на выносливость по контактным напряжениям по формуле где T1 – крутящий момент на шестерне в Н•м, КН – коэффициент контактной нагрузки, Коэффициент ширины зубчатого венца выбирают из ряда по ГОСТ 2185-66: при симметричном расположении шестерни относительно опор Коэффициент контактной нагрузки вычисляют по формуле КН = KHα KHβ КНV, ( 5 ) где KHα - коэффициент неравномерности распределения нагрузки между зубьями, KHβ – коэффициент неравномерности распределения нагрузки по ширине колеса, КНV – динамический коэффициент. Для определения этих коэффициентов необходимо знать размеры передачи. Поскольку на данном этапе проектного расчета размеры не известны, то рекомендуется задавать приближенное значение КН=1.2. Полученное по формуле ( 4 ) значение Z где Полученное значение Z Далее определяют число зубьев шестерни Z1= Если Z1 Z1< Z1min , то коэффициент смещения шестерни определяют по формуле x1= Ширину венца колеса определяют по формуле bw2= Ширину венца шестерни bw1 принимают на 2…5 мм больше чем bw2. Определяют диаметры окружностей зубчатых колес, принимая далее для непрямозубых колес m=mn: делительные окружности прямозубых колес dj=mZj, косозубых колес окружности вершин зубьев daj = dj+2 m (1+xj), окружности впадин зубьев dfj = dj-2 m (1.25- xj). Вычисляют окружную скорость в зацеплении: V= По табл.8 назначают степень точности передачи.
Таблица 8 Степень точности передачи.
Степень точности nст=9 для закрытых зубчатых передач применять не рекомендуется.
4.Проверочный расчет передачи Условие контактной прочности передачи имеет вид напряжения
где Z КН - коэффициент контактной нагрузки, определяется по формуле ( 5 ). Коэффициент неравномерности распределения нагрузки между зубьями равен KHα =1+A•(nст-5)•К где А=0.06 для прямозубых и А=0.15 для косозубых и шевронных передач, К Таблица 9 Коэффициент K
Таблица 10 Значения коэффициента KHV
Примечание: в числителе значения для прямозубых передач, в знаменателе для непрямозубых.
Для плохо прирабатывающихся зубчатых колес с твердостью поверхности зуба НВ2>350 принимают К К где V-окружная скорость в зацеплении. Динамический коэффициент КНV определяется по табл.10 . Коэффициент неравномерности распределения нагрузки по ширине колеса равен KHβ = 1+ (K где K В таблице значение K Допускается перегрузка по контактным напряжениям не более 5%, рекомендуемая недогрузка до 15%. Если указанные условия не выполняются, то следует либо изменить межосевое расстояние передачи, либо изменить Условия изгибной прочности передачи имеют вид sFj
где YFj - коэффициенты формы зуба, КF - коэффициент нагрузки при изгибе, Yb - коэффициент, учитывающий влияние угла наклона зуба на его прочность, Yb=1 для прямозубых передач, Yb=0.52 для косозубых передач и Yb=0.48 для шевронных передач. Напряжение изгиба в зубьях колеса равно:
Коэффициенты формы зуба даны в ГОСТ 21354-87 в виде графиков, которые аппроксимируются зависимостью: YFj=3.47+ где ZVj - эквивалентное число зубьев, для прямозубых передач ZVj= Zj, для непрямозубых передач ZVj= Коэффициент нагрузки при изгибе определяют по формуле: KF = KFα KFβ KFV. Коэффициенты, входящие в эту формулу, имеют такой же физический смысл, что и коэффициенты в формуле для КН. Для их определения используют следующие зависимости: KFα =1 для прямозубых передач, KFα=1+A•(nст-5) для непрямозубых передач, KFβ = 0.18+0.82 K Допускается перегрузка по напряжениям изгиба не более 5%, недогрузка не регламентируется. Если перегрузка более 5% следует увеличить модуль передачи и повторить расчет.
5. Силы в зацеплении Окружная сила Ft= Приложения Таблица 11 Электродвигатели асинхронные серии 4А, закрытые обдуваемые (по ГОСТ 19523-81)
Таблица 12 Значения КПД механических передач
Примечание: КПД пары подшипников качения

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , Sm= 1.2•
, Sm= 1.2• 
 , ( 1 )
, ( 1 )
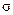 HPj=
HPj=  ,
, 
 1, ( 2 )
1, ( 2 ) KHLmax, значения KHLmax даны в табл 5.
KHLmax, значения KHLmax даны в табл 5. h•NΣj, ,
h•NΣj, , ,
,
 106 – базовое число циклов при изгибе, NFEj – эквивалентное число циклов напряжений при изгибе.
106 – базовое число циклов при изгибе, NFEj – эквивалентное число циклов напряжений при изгибе. =
= 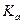 •(u + 1)
•(u + 1)  , ( 4 )
, ( 4 ) - коэффициент ширины зубчатого венца.
- коэффициент ширины зубчатого венца. и округляют до стандартного значения по табл.1. Модуль меньше 2 мм для силовых передач применять не рекомендуется. В косозубых передачах стандартизован нормальный модуль mn. Далее определяют суммарное число зубьев. Для прямозубых передач Z
и округляют до стандартного значения по табл.1. Модуль меньше 2 мм для силовых передач применять не рекомендуется. В косозубых передачах стандартизован нормальный модуль mn. Далее определяют суммарное число зубьев. Для прямозубых передач Z  =
= 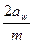 . Рекомендуется сочетание
. Рекомендуется сочетание  =
= 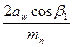 ,
, =12
=12  для косозубых передач и
для косозубых передач и  = arccos
= arccos  .
. и округляют его до ближайшего целого числа. Находят число зубьев колеса Z2= Z
и округляют его до ближайшего целого числа. Находят число зубьев колеса Z2= Z  . Значение uф не должно отличаться от номинального более чем на 2.5% при u
. Значение uф не должно отличаться от номинального более чем на 2.5% при u  . Для прямозубых передач Z1min=17, для непрямозубых - Z1min=17•cos3
. Для прямозубых передач Z1min=17, для непрямозубых - Z1min=17•cos3 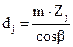 ,
, .
.

 ,
, = 9600 для прямозубых и Z
= 9600 для прямозубых и Z 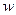 ,
, для одноступенчатых редукторов
для одноступенчатых редукторов

 ,
,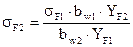 .
. +0.092•
+0.092•  ,
, .
. . Распорная сила: в прямозубых передачах Fr= Fttg
. Распорная сила: в прямозубых передачах Fr= Fttg  , в непрямозубых передачах Fr= Ft•
, в непрямозубых передачах Fr= Ft•  . Осевая сила в косозубых передачах Fа= Ft•tg
. Осевая сила в косозубых передачах Fа= Ft•tg  .
. =0.99.
=0.99.