
|
|
Модель оптимального экономического ростаРрассмотрим траекторию экономического роста с точки зрения аспекта потребления. По существу, экономическая траектория - это кривая изменения (фазового) состояния экономики во времени под воздействием различных управляемых и неуправляемых факторов. Если не принимать во внимание существование непредсказуемых факторов, то можно говорить, что рычаги управления экономикой принадлежат ее участникам: одни - потребителям, вторые - производителям, третьи - государству. Каждый управляет своими рычагами, исходя из собственного интереса. Под воздействием управляющих параметров вектор состояния экономики приходит в движение, т.е. описывает некоторую кривую в фазовом пространстве (в пространстве состояний). Причем каждому «положению» этих рычагов соответствует своя траектория. Задача экономического управления (планирования) заключается в том, чтобы была реализована наиболее эффективная (оптимальная) траектория. Известно достаточно много желательных условий, которые можно предъявить к экономической траектории. Это и конкурентная равновесность, это и соответствие максимальному сбалансированному темпу роста (т.е. «магистральность»), это и оптимальность в смысле максимизации или минимизации какой-либо целевой функции. Актуальность исследования моделей роста должна будет подняться на новый уровень в связи со становящейся все более популярной в последнее время концепцией устойчивого развития человеческого общества. Суть устойчивого развития можно пояснить, как стремление общества к удовлетворению потребностей ныне живущих людей без лишения возможности будущих поколений удовлетворять свои потребности. Учет этой концепции при разработке долгосрочного экономического плана развития предполагает разрешение дилеммы, связанной с распределением благ на настоящее и будущее потребление. Обеспечение будущего потребления принято называть инвестициями или капитальными вложениями. С точки зрения настоящего момента более высокий уровень потребления предпочтительнее более низкого. Однако высокий уровень потребления влечет меньшие капитальные вложения (на будущее потребление). Поэтому вдоль траектории экономического роста возникает задача выбора оптимальной политики потребления. Так мы приходим к задаче об оптимальном с точки зрения потребления экономическом росте. Ее мы будем формализовать как динамическую оптимизационную модель и анализировать с помощью понятий математической теории оптимального управления. По своей сути задача об оптимальных пропорциях потребления и инвестиций больше относится к макроэкономике, т.е. к агрегированным моделям. Поэтому ее мы смоделируем для экономики, производящей один (национальный) продукт с использованием двух основных факторов производства - труда и капитала (основных производственных фондов). На таком макроуровне все величины представляются в их стоимостном измерении. Поэтому валовый продукт ассоциируется с национальным доходом, а потребление и инвестиции составляют национальные расходы. Можно представить следующую схему распределения национального дохода:
Рис. 6.1 Схема распределения национального дохода
Введем необходимые обозначения. Согласно общепринятой традиции для агрегированных моделей Для упрощения модели будем предполагать, что в рассматриваемом (планируемом) периоде времени Пусть валовый выпуск определяется с помощью агрегированной производственной функции
Отсутствие технического прогресса означает, что производственная функция F инвариантна во времени. Относительно нее будем предполагать выполненными закон об убывающей доходности (см. (3.2.2), (3.2.3)) и свойство однородности первой степени, т.е.
Бюджетный баланс требует, чтобы в каждый год t выполнялось равенство
Равенство (6.3.2) отражает соответствие расходов общества его доходам и показывает, что на макроуровне ежегодно весь национальный доход делится на потребление и инвестиции, т.е. между настоящим и будущим потреблением. Обозначим через
Как следует из рис.6.1, валовые капитальные вложения, в свою очередь, идут на увеличение наличного капитала с целью приращения основных фондов (чистые капитальные вложения) и на замещение изношенного капитала, т.е. на восстановление изношенной части основных производственных фондов (амортизационные отчисления). Предположим, что основные фонды изнашиваются с темпом
Отсюда получаем динамику чистого капитального вложения (уравнения движения основных фондов)
где Для построения требуемой модели оптимального экономического роста в виде задачи оптимального управления нам нужно ввести понятия фазового состояния экономики, управляющих параметров, построить уравнение движения, определить начальное состояние и критерий качества (целевой функционал). Такую модель называют неоклассической моделью оптимального экономического роста. Чтобы определить перечисленные элементы модели, оперируют «экономическими нормами», приходящимися на одного рабочего (на одну единицу трудовых ресурсов). Для перехода к новой терминологии, связанной с нормами на одного рабочего, положим коэффициент однородности
Отношение Обозначим объем валового выпуска и фондовооруженность, приходящиеся на одного рабочего, соответственно через
и введем новую производственную функцию
Тогда вместо (6.3.1) можно написать Соответствующим образом введем величину потребления и инвестиций, приходящиеся на одного рабочего:
В новых обозначениях баланс (6.3.2) примет вид
а равенство (6.3.3) для валовых инвестиций –
(здесь мы положили Подставляя в (6.3.4) выражение для инвестиций (6.3.5), получаем
Равенство (6.3.6) показывает, что выпуск продукции, приходящийся на одного рабочего, распределяется на три составные части: потребление на данного рабочего, поддержание (амортизацию) его капиталовооруженности на прежнем уровне и чистый прирост капиталовооруженности рабочего. Уравнение (6.3.6) называется основным (разностным) уравнением неоклассической модели экономического роста. Приведем геометрическую интерпретацию основного уравнения (рис. 6.2). Перепишем основное уравнение в виде
Рис. 6.2 Геометрическая иллюстрация основного уравнения
На рис. 6.2 график функции Случай a) не имеет экономически осмысленной интерпретации и приводится для полноты математических рассуждений, как один из крайних случаев распределения национального дохода, предполагающий направление всего дохода на инвестиции. В случае b) максимальный уровень потребления
и называется уровнем золотого правила накопления. При этом максимальный уровень потребления
(когда В неоклассических моделях роста под состоянием экономики (фазовой координатой системы) принято понимать фондовооруженность на одного рабочего
Получили закон изменения фондовооруженности во времени. Предположим, что в начальный момент
С точки зрения макроэкономического управления, управляющим параметром является потребление на одного рабочего
Заметим, что слева берется нестрогое неравенство ради замкнутости множества значений управляющего параметра в каждый момент времени, без чего оптимальное управление может и не существовать. Множество всех допустимых управлений обозначим символом Для окончательного построения оптимизационной модели остается сконструировать соответствующий содержанию рассматриваемой задачи функционал качества, оценивающий уровень достижения той или иной экономической цели. С учетом агрегированности модели такая цель должна быть глобальной и нацеленной на повышение благосостояния общества. Так как попытка определения совокупной функции полезности для общества в целом сопряжена с рядом сложностей, о которых подробно говорилось в разделе 4.2, то в качестве целевого функционала в макромодели рассматривают функцию полезности u, оценивающую уровень потребления одного (обобщенного) рабочего. Целевой функционал обычно задается на множестве допустимых траекторий системы (6.3.8)-(6.3.10). Однако такое определение здесь не учитывает специфику понятия полезности применительно к долгосрочному планированию. Действительно, для динамической системы (6.3.8)-(6.3.10) введем понятие терминального множества, которое обозначим буквой Допустимой траекторией динамической системы (6.3.8)-(6.3.9) называется всякая последовательность
Теперь можно формализовать выбор оптимального управления системой (6.3.8)-(6.3.9) следующим образом. Планирующий орган выбирает некоторое допустимое управление
Из этого множества траекторий представляют интерес только те, которые приводят систему в заранее заданное терминальное множество
Оптимальной траекторией системы (6.3.8)-(6.3.10) называется такая траектория Задание функции полезности вдоль допустимой траектории означает, что
где С учетом того, что потребление Коэффициент дисконтирования отражает предпочтительность близких во времени потреблений. Согласно схеме дисконтирования, функцию полезности от потребления нужно определить в каждый год и в качестве целевого функционала, оценивающего уровень потребления на всем интервале
где Окончательно неоклассическая модель агрегированной задачи оптимального экономического роста в целом имеет вид:
Эту же модель иногда называют задачей рационального ведения хозяйства. Допустимое управление
а

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 будет означать валовый выпуск в год
будет означать валовый выпуск в год  ,
,  - объем потребления,
- объем потребления, 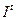 - инвестиции (валовые капитальные вложения),
- инвестиции (валовые капитальные вложения),  - трудовые ресурсы,
- трудовые ресурсы, 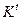 - капитал (основные фонды).
- капитал (основные фонды).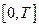 импорта и экспорта нет, и технический прогресс отсутствует. Подчеркнем, что обобщение модели с учетом этих важных условий функционирования экономики не составляет труда, но загромождает модель.
импорта и экспорта нет, и технический прогресс отсутствует. Подчеркнем, что обобщение модели с учетом этих важных условий функционирования экономики не составляет труда, но загромождает модель. :
: (6.3.1)
(6.3.1)
 (6.3.2)
(6.3.2) долю инвестиций в национальном доходе в год
долю инвестиций в национальном доходе в год 

 , т.е. за год
, т.е. за год  единиц основных фондов. В силу обозначений
единиц основных фондов. В силу обозначений  характеризуют основные фонды в начале и в конце периода
характеризуют основные фонды в начале и в конце периода  . Следовательно, приращение основных фондов за год есть
. Следовательно, приращение основных фондов за год есть  Поэтому объем инвестиций должен удовлетворять условию
Поэтому объем инвестиций должен удовлетворять условию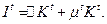 (6.3.3)
(6.3.3)

 - начальные вложения в основные фонды, а
- начальные вложения в основные фонды, а  - горизонт планирования. Это есть аналог основного уравнения экономического роста в агрегированных показателях.
- горизонт планирования. Это есть аналог основного уравнения экономического роста в агрегированных показателях. производственной функции
производственной функции  , т.е.
, т.е.  . Это число можно определить как «доля одного рабочего от целого» в момент
. Это число можно определить как «доля одного рабочего от целого» в момент  или
или
 называется, (см. раздел 3.3), фондовооруженностью или капиталовооруженностью и показывает долю основных фондов или долю капитала, приходящуюся на одного рабочего.
называется, (см. раздел 3.3), фондовооруженностью или капиталовооруженностью и показывает долю основных фондов или долю капитала, приходящуюся на одного рабочего. и
и  :
:

 :
:



 (6.3.4)
(6.3.4) (6.3.5)
(6.3.5) ).
). (6.3.6)
(6.3.6) (6.3.7)
(6.3.7)
 получен как разность графиков функций
получен как разность графиков функций  и
и  В точке
В точке 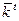 достигается максимальное значение этой функции, а в точке
достигается максимальное значение этой функции, а в точке  она равна нулю. Благодаря предположению об убывающей доходности относительно функции
она равна нулю. Благодаря предположению об убывающей доходности относительно функции  )нулевой уровень потребления на одного рабочего
)нулевой уровень потребления на одного рабочего  ; b) максимальный объем потребления на одного рабочего (
; b) максимальный объем потребления на одного рабочего (  ); c) потребление рабочего на фиксированном уровне
); c) потребление рабочего на фиксированном уровне 

 соответствует точке
соответствует точке 

 ) и называется уровнем золотого правила потребления. В промежуточном случае c) линия потребления на одного рабочего
) и называется уровнем золотого правила потребления. В промежуточном случае c) линия потребления на одного рабочего  и
и  . Это есть два состояния «равновесия», из которых наиболее предпочтительным является
. Это есть два состояния «равновесия», из которых наиболее предпочтительным является  . Поэтому уравнение движения должно быть построено относительно этого параметра. Нужный закон движения получим из основного уравнения экономического роста (6.3.6), переписав его в виде
. Поэтому уравнение движения должно быть построено относительно этого параметра. Нужный закон движения получим из основного уравнения экономического роста (6.3.6), переписав его в виде
 (6.3.8)
(6.3.8) эта величина задана и равна
эта величина задана и равна 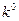 :
: (6.3.9)
(6.3.9) По правилам теории оптимального управления необходимо определить класс допустимых управлений для системы (6.3.8)-(6.3.9). Допустимым управлением будем называть любую последовательность
По правилам теории оптимального управления необходимо определить класс допустимых управлений для системы (6.3.8)-(6.3.9). Допустимым управлением будем называть любую последовательность  которая в каждый момент t удовлетворяет условию
которая в каждый момент t удовлетворяет условию

 . Это подмножество фазового пространства
. Это подмножество фазового пространства  системы (6.3.8) -(6.3.9), состоящее из тех его точек, в которые желательно привести состояние экономики к плановому горизонту
системы (6.3.8) -(6.3.9), состоящее из тех его точек, в которые желательно привести состояние экономики к плановому горизонту  удовлетворяющая уравнению (6.3.8) и такая, что
удовлетворяющая уравнению (6.3.8) и такая, что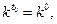

 Подставляя это управление и начальное состояние (6.3.9) в правую часть уравнения движения (6.3.8), находим соответствующую траекторию
Подставляя это управление и начальное состояние (6.3.9) в правую часть уравнения движения (6.3.8), находим соответствующую траекторию  Каждому управлению соответствует своя траектория. Таким образом, множеству допустимых управлений соответствует множество всех траекторий системы (6.3.8)-(6.3.9):
Каждому управлению соответствует своя траектория. Таким образом, множеству допустимых управлений соответствует множество всех траекторий системы (6.3.8)-(6.3.9):

 вдоль которой функционал качества (функция полезности) принимает максимальное значение.
вдоль которой функционал качества (функция полезности) принимает максимальное значение. (или в более общем случае
(или в более общем случае  ), так что
), так что 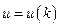 , где
, где  Так как требуется с помощью функции
Так как требуется с помощью функции 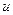 оценить потребление (а не фондовооруженность), то, во-первых, мы должны определить ее на множестве
оценить потребление (а не фондовооруженность), то, во-первых, мы должны определить ее на множестве  допустимых управлений:
допустимых управлений: т.е.
т.е. 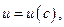
 Во-вторых, и это самое главное, полезность
Во-вторых, и это самое главное, полезность  не учитывает несовпадение оценок полезностей от потребления товаров в различные моменты времени. Поскольку план развития экономики составляется в начальный момент времени
не учитывает несовпадение оценок полезностей от потребления товаров в различные моменты времени. Поскольку план развития экономики составляется в начальный момент времени  на весь период
на весь период  . Для этого надо дожить до момента
. Для этого надо дожить до момента  с точки зрения начального момента
с точки зрения начального момента 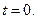
 т.е. через
т.е. через  (в момент
(в момент  Из этой формулы получаем
Из этой формулы получаем  Это есть оценка потребления в момент
Это есть оценка потребления в момент 
 (6.3.11)
(6.3.11)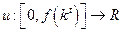 - определенная на множестве допустимых уровней потребления в год
- определенная на множестве допустимых уровней потребления в год  (6.3.12)
(6.3.12) соответствующее максимальному значению функционала (6.3.11), называется оптимальным управлением. Оно определяет оптимальный уровень потребления
соответствующее максимальному значению функционала (6.3.11), называется оптимальным управлением. Оно определяет оптимальный уровень потребления  Поэтому для каждого фиксированного значения
Поэтому для каждого фиксированного значения  трудовых ресурсов можно найти оптимальные пропорции
трудовых ресурсов можно найти оптимальные пропорции 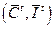 потребления и инвестиций, где
потребления и инвестиций, где
 задачи (6.3.12).
задачи (6.3.12).