
|
|
Модель регулирования цен и устойчивость конкурентного равновесияДоказав существование конкурентного равновесия в математической модели рынка, ответим на вопрос: как найти конкурентное равновесие и, прежде всего, равновесные цены? Поиск равновесия, в отличие от ранее рассмотренных вопросов, по существу, является динамическим (развернутым во времени) действием. Процесс последовательного приближения к равновесной цене называется регулированием цен. Кто и с какой целью регулирует цены? Ответ заключается в том, что, благодаря законам спроса и предложения, в условиях конкуренции рынок сам приспосабливает цены к вариациям спроса и предложения во времени. Ранее была обнаружена геометрическая картина такого приспособления. В данном случае задача состоит в обнаружении аналитической формулы регулирования для численного вычисления равновесных цен. Итеративный процесс поиска равновесных цен должен обладать свойством сходимости, т.е., в конечном счете, должен привести к искомым ценам с любой предзаданной точностью. В этом случае процесс регулирования цен (или собственно конкурентное равновесие) называется устойчивым. Таким образом, задача регулирования цен преследует цель определения условий, заставляющих цены, как функций времени, сходиться к равновесным значениям. Математически эта задача сводится к нахождению условий устойчивости решений специально построенных рекуррентных по времени уравнений. Такое уравнение называется динамической моделью регулирования цен. Эта модель может быть как непрерывной, так и дискретной. В первом случае, на основе предположения о непрерывном изменении цен, модель выражается с помощью дифференциальных уравнений. Во втором случае предполагается дискретный характер изменения цен, т.е. фиксируется изменение цен в отдельные моменты времени (или через определенные промежутки времени). Поэтому модель регулирования цен имеет вид разностных уравнений. Непрерывные модели предпочтительны в теоретическом плане. Их преимущество состоит в возможности применения удобного аппарата дифференцирования. В дальнейшем будем рассматривать только дискретный случай. Для определенности процесс регулирования рассмотрим в модели Эрроу-Дебре. Предварительно уточним некоторые предпосылки и ряд дополнительных сведений. Во-первых, цены будем снабжать параметром времени Во-вторых, будем предполагать дискретное изменение времени, т.е. будем рассматривать отдельные моменты времени В-третьих, вместо пространства товаров Для некоторого вектора цен
Величина Для равновесного вектора цен имеем (см. (4.3.7), (4.3.8))
Если предположить что все цены строго положительными, т.е.
Так как это равенство понимается покомпонентно Функция F обычно предполагается положительно однородной нулевой степени, т.е. для любых Рассмотрение функции избыточного спроса связано с ее применением в модели регулирования цен. В основе построения искомой формулы итеративного процесса вычисления равновесных цен лежит идея о том, что скорость изменения цен пропорциональна изменению величины избыточного спроса. Действительно, возрастание (убывание) функции избыточного спроса во времени равносильно более быстрому (медленному) росту спроса по сравнению с предложением (см. (4.5.1)), а это, согласно закона спроса, сопровождается увеличением (уменьшением) цен товаров. Математически это можно выразить формулой
или в координатной форме
где Из последнего уравнения по определению производной (см. (2.2.3)) получаем:
Отсюда для достаточно малых
Принимая величину
или в векторной форме:
Получили рекуррентное уравнение, когда последующее (по времени) значение цены вычисляется с помощью предыдущего значения. Для его последовательного решения нужно иметь начальное условие. Им является значение цены Для того чтобы в уравнении (4.5.5) было учтено условие положительности цен, можно написать
Таким образом, динамика процесса регулирования цен описана. Процесс регулирования можно проводить в нормированных ценах или без нормирования цен. В первом случае вектор Устойчивость конкурентного равновесия, т.е. сходимость итеративного процесса (4.5.6) к равновесной цене, можно изучать на двух уровнях - на уровне локальной устойчивости и на уровне глобальной устойчивости. Равновесие называется локально устойчивым, если итеративный процесс сходится при начальной точке Одним из условий сходимости процесса (4.5.6) является так называемая строгая валовая зависимость. Говорят, что для ненормированного процесса регулирования цен имеет место строгая валовая зависимость, если для каждого k функция избыточного спроса Приведём без доказательства теорему сходимости для уравнения (4.5.6), которая предполагает ненормированный процесс регулирования и содержит критерий глобальной устойчивости. Теорема 4.3.Пусть 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
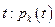 - цена k-го товара в момент t.
- цена k-го товара в момент t.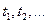 Причем для упрощения формул будем считать, что
Причем для упрощения формул будем считать, что  Это дает возможность вместо последовательности
Это дает возможность вместо последовательности 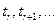 рассматривать последовательность моментов
рассматривать последовательность моментов  начиная с
начиная с 
 будем рассматривать пространство
будем рассматривать пространство 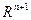 , где дополнительная
, где дополнительная  -ая координата соответствует особому виду товара - деньгам. Таким образом, размерность всех векторов спроса и предложения будет равна
-ая координата соответствует особому виду товара - деньгам. Таким образом, размерность всех векторов спроса и предложения будет равна  . Причем дополнительная
. Причем дополнительная 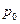 будет интерпретироваться как цена денег.
будет интерпретироваться как цена денег. и соответствующих ему векторов совокупного спроса
и соответствующих ему векторов совокупного спроса  и совокупного предложения
и совокупного предложения  обозначим
обозначим (4.5.1)
(4.5.1) имеет смысл избыточного спроса при ценах p (противоположная величина
имеет смысл избыточного спроса при ценах p (противоположная величина  имеет смысл избыточного предложения). Рассматривая эту величину для всех
имеет смысл избыточного предложения). Рассматривая эту величину для всех  , (4.5.2)
, (4.5.2) (4.5.3)
(4.5.3) то равенство (4.5.3) будет иметь место только в случае строгого равенства в (4.5.2) , т.е.
то равенство (4.5.3) будет иметь место только в случае строгого равенства в (4.5.2) , т.е. (4.5.4)
(4.5.4)
 , где
, где  - функция избыточного спроса для товара k), то условие (4.5.3) становится следствием равенства (4.5.4). Поэтому в случае положительных цен конкурентное равновесие определяется одним условием (4.5.4) .
- функция избыточного спроса для товара k), то условие (4.5.3) становится следствием равенства (4.5.4). Поэтому в случае положительных цен конкурентное равновесие определяется одним условием (4.5.4) . и постоянного числа
и постоянного числа 
 Это свойство означает, что на функцию избыточного спроса изменение масштаба цен не влияет, а существенны лишь относительные цены.
Это свойство означает, что на функцию избыточного спроса изменение масштаба цен не влияет, а существенны лишь относительные цены.

 - коэффициент пропорциональности,
- коэффициент пропорциональности,  - функция избыточного спроса для товара k . Здесь предполагается, ради простоты, что пропорциональность изменения цены и избыточного спроса по всем товарам одинакова (и равна числу
- функция избыточного спроса для товара k . Здесь предполагается, ради простоты, что пропорциональность изменения цены и избыточного спроса по всем товарам одинакова (и равна числу 
 можно принять приблизительно
можно принять приблизительно
 как следующий за t момент времени, для дискретного случая мы приходим к следующему закону изменения цен:
как следующий за t момент времени, для дискретного случая мы приходим к следующему закону изменения цен:
 (4.5.5)
(4.5.5) в начальный момент времени
в начальный момент времени 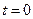 , которое считается известным.
, которое считается известным.
 нормируется с помощью какого-то выделенного товара (например, нулевого), и получается новый вектор
нормируется с помощью какого-то выделенного товара (например, нулевого), и получается новый вектор  компоненты которого
компоненты которого  являются относительными ценами. В ненормированном процессе все товары являются равноправными. С математической точки зрения ненормированный процесс усложняется множественностью равновесных векторов цен, так как все точки луча
являются относительными ценами. В ненормированном процессе все товары являются равноправными. С математической точки зрения ненормированный процесс усложняется множественностью равновесных векторов цен, так как все точки луча  будут равновесными векторами цен.
будут равновесными векторами цен. , достаточно близкой к
, достаточно близкой к 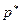 . Если устойчивость имеет место независимо от местонахождения начальной точки
. Если устойчивость имеет место независимо от местонахождения начальной точки  Экономический смысл этого условия состоит в том, что при повышении цены
Экономический смысл этого условия состоит в том, что при повышении цены  -го товара и постоянстве других цен можно ожидать увеличения спроса на остальные (взаимозаменимые) товары.
-го товара и постоянстве других цен можно ожидать увеличения спроса на остальные (взаимозаменимые) товары. , что для всех
, что для всех  система цен
система цен  , удовлетворяющая уравнению (4.5.6), сходится к равновесному вектору цен.
, удовлетворяющая уравнению (4.5.6), сходится к равновесному вектору цен.