
|
|
Экономическое равновесие. Содержательный аспектГлава 4. Математическая теория конкурентного равновесия
Экономическое равновесие. Содержательный аспект
Рассмотрим взаимодействие субъектов микроэкономики – потребителя и фирмы в процессе образования более крупной структуры - рынка. Взаимодействие между складывающимися на рынке готовой продукции потребительским спросом и предложением фирм приводит к понятию равновесия. Равновесие в общепринятом в экономике смысле, как равенство спроса и предложения, было определено при рассмотрении основных рыночных категорий. Это наиболее важная, но все же узкая (частная) трактовка понятия равновесия, предполагающая наличие уравнивающих друг друга факторов. О равновесии можно говорить в общем случае, как о характеристике состояния любой системы, на которую воздействуют различные стороны (в частности, только одна сторона), каждая со своими интересами. В таком общем смысле равновесие - это такое состояние системы, которое устраивает всех заинтересованных в ее состоянии сторон, за неимением ничего лучшего. Приведем несколько конкретных понятий равновесия. 1. Равновесие в задачах принятия решения со многими участниками. Предположим, что интересы участников (лиц, принимающих решения) не противоположны, но и не совпадают. Однако степень достижения своей цели каждым из них зависит как от его собственных решений, так и от действий всех остальных участников. Под равновесным состоянием данной системы понимается такая ситуация (совокупность выбранных решений), когда отклонение от этой ситуации только ухудшает положение уклониста (при условии, что остальные участники придерживаются этой ситуации). Равновесная ситуация не обеспечивает участникам наилучшее достижение цели, но, если такая ситуация существует, то, в условиях отсутствия обмена информациями участникам ничего другого не остается, как придерживаться ее (во избежании худшего). Это так называемое равновесие по Нэшу. Оно широко применяется в теории игр - разделе исследования операций, посвященном математическим моделям задач принятия решения в условиях конфликта и неопределенности. 2. Равновесные действия противоборствующих сторон. Такая ситуация предполагает наличие двух лиц, принимающих решения, с прямо противоположными интересами (например, две конкурирующие фирмы, выпускающие один и тот же товар, имеющие один и тот же рынок сбыта). Здесь каждая сторона выбирает лучшее из тех решений, которые разрешены ее противником. Равновесным является то состояние, одностороннее отклонение от которого невыгодно уклонисту. Такое равновесие называется седловой точкой и, если оно существует, то противники вынуждены ее придерживаться. Очевидно, седловая точка является частным случаем равновесия по Нэшу. 3. Равновесие на основе угроз. Этот принцип применяется в задачах принятия решения с обменом информацией. Равновесным называется такое состояние системы, когда любое мотивированное предложение (угроза) одних участников, направленное на изменение данного состояния системы, встречает мотивированное возражение (контругрозу) со стороны других участников. 4. Равновесие в задаче потребителя.Как известно, наилучшее состояние потребителя описывается точками, в которых бюджетные линии касаются соответствующих кривых безразличия. Эти точки характеризуют спрос, во-первых, как платежеспособную потребность в товарах, во-вторых, как набор товаров, максимизирующий полезность потребителя. Отклоняясь от них в своем выборе, потребитель нарушает одно из условий оптимальности. Поэтому данные точки и отражают равновесное состояние потребителя. Аналитически это состояние характеризуется равенством между отношением цен товаров и предельной нормой замещения (см. (2.4.10)). 5. Равновесие в задаче фирмы. Условия равновесия в задаче фирмы концептуально схожи с соотношениями, формируемыми в теории спроса. Цель фирмы - максимизация прибыли (или минимизация издержек) при ограниченных ресурсах (при фиксированном уровне выпуска). Набор затрат ресурсов, удовлетворяющих этим условиям, и отражает равновесное состояние производства. Реализация других объемов затрат может привести лишь к нарушению условий оптимальности. Аналитически состояние равновесия фирмы выражается равенством между отношением цен на соответствующие факторы производства и готовый продукт и предельной нормой замещения. Характерным свойством равновесий в приведенных примерах является их устойчивость против отклонения. Присуще ли это свойство экономическому равновесию? Для ответа на этот вопрос, рассмотрим рынок одного товара, относительно которого будем говорить о совокупном спросе потребительского сектора и о совокупном предложении производственного сектора, не уточняя пока эти категории и оставляя их понимание на интуитивном уровне. Пусть цена товара фиксирована. Это положение соответствует условиям совершенной конкуренции, когда отдельные участники экономики не влияют на цену товара. Пусть имеет место равновесие: Рассмотрим сначала неценовые причины (вызванные влиянием сезонности, моды, изменением экономической политики и т.д.). Предположим, что при неизменном предложении потребитель сознательно отклоняется от равновесия, увеличивая или уменьшая спрос: a) Если при фиксированном спросе от равновесия отклоняется производитель, то соответственно придем к одному из двух неравенств: c) В этих соотношениях случаи a) и c) приводят к дефициту (см. Рис. 1.2), т.е., в конечном счете, к повышению цены, что выгодно производителю и невыгодно потребителю. Следовательно, в случаях a) и c) неценовые причины вызывают изменение равновесной.
Рис. 4.1 Устойчивость равновесия против колебания цен
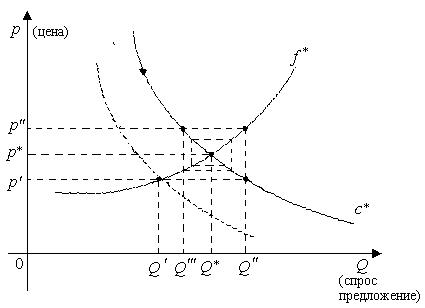
цены. Случаи b) и d) приводят к излишкам (см. Рис.1.2), т.е., в конечном счете, к снижению цены, что выгодно потребителю и невыгодно производителю. Следовательно, в случаях b) и d) неценовые причины также вызывают изменение равновесной цены. Исходя из таких рассуждений, можно было бы заключить, что потребителю выгодно отклонение от равновесия в сторону снижения спроса, а производителю - в сторону снижения предложения. Однако для достоверности таких утверждений необходимо ответить на следующие вопросы. На сколько нужно уменьшить спрос, чтобы соответствующее снижение цены действительно было выгодно для потребителя, т.е. чтобы сэкономленные средства с остатком компенсировали ущерб от уменьшения спроса? Каким должен быть этот остаток? Аналогичные вопросы возникают и для определения конкретной выгоды производителя. Ответы на эти вопросы можно дать, применяя понятие предельной нормы замещения. Очевидно, по отношению к экономическому равновесию однозначно нельзя утверждать о его устойчивости против отклонения. Но зато эти рассуждения помогают обнаружить устойчивость другого характера - тенденцию экономического равновесия к устойчивости против колебания цены, какой бы причиной оно ни было вызвано. Поясним это положение. Будем исходить из того факта, что экономическое равновесие может быть нарушено как по ценовым, так и по неценовым причинам. Пусть на уровне цен
т.е. спрос стал больше предложения. Цене Для того чтобы точка Обсудим ценовую причину. Пусть цена товара упала до величины В результате можно сделать вывод о том, что экономическое равновесие устойчиво против ценовых возмущений. Паутинообразная модель описывает приспособление цены во времени к вариациям спроса и предложения. Опишем ее детально на примере линейных функций. Пример 4.1. Для рынка одного товара выведем формулу паутинообразного регулирования цены при условии, что функции спроса и предложения линейно зависят от цены, и предложение реагирует на изменение спроса с временным лагом (с опозданием на некоторый промежуток времени). Линейность функций спроса и предложения означает, что их можно представить в виде:
Рис. 4.2 Паутинная модель
Пусть Отсюда получаем искомую рекуррентную формулу приспособления цены к уровням спроса и предложения:
Зная начальную цену Заметим, что когда

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
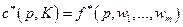 , где
, где  - совокупный спрос,
- совокупный спрос,  - совокупное предложение, p - цена товара, k - доход потребительского сектора,
- совокупное предложение, p - цена товара, k - доход потребительского сектора, 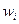 - цены затрат. Формально это равновесие может быть нарушено либо по воле рынка, который распоряжается ценой товара, либо по воле покупателя (управляющего спросом, например, посредством изменения величины дохода) или производителя (управляющего предложением, например, посредством изменения объемов затрат). В первом случае говорят о ценовых причинах нарушения равновесия, во втором - о неценовых причинах.
- цены затрат. Формально это равновесие может быть нарушено либо по воле рынка, который распоряжается ценой товара, либо по воле покупателя (управляющего спросом, например, посредством изменения величины дохода) или производителя (управляющего предложением, например, посредством изменения объемов затрат). В первом случае говорят о ценовых причинах нарушения равновесия, во втором - о неценовых причинах. b)
b) 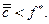
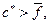 d)
d) 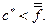
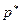 имеет место равновесие
имеет место равновесие 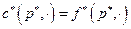 (точки здесь заменяют прочие, в частности, неценовые, переменные). Допустим, что по какой-то неценовой причине повысился спрос до уровня
(точки здесь заменяют прочие, в частности, неценовые, переменные). Допустим, что по какой-то неценовой причине повысился спрос до уровня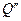 . Как следует Рис. 4.1 , спрос
. Как следует Рис. 4.1 , спрос 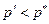 . Поэтому
. Поэтому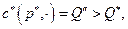
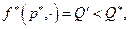
 соответствуют две точки:
соответствуют две точки: 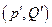 и
и 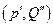 . Естественно поставить вопрос: может ли цена
. Естественно поставить вопрос: может ли цена 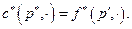 Содержательно, бюджет потребителя должен уменьшиться ровно на величину
Содержательно, бюджет потребителя должен уменьшиться ровно на величину 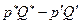 , и тогда бюджетная линия в пространстве товаров параллельно сместится от точки
, и тогда бюджетная линия в пространстве товаров параллельно сместится от точки 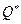 до точки
до точки 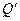 . Такое изменение ситуации приведет к уменьшению дохода производителя
. Такое изменение ситуации приведет к уменьшению дохода производителя  , и оно вызвано двумя причинами: снижением цены
, и оно вызвано двумя причинами: снижением цены 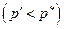 и выпуска
и выпуска 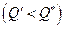 . Что может противопоставить этому производитель? При данных неизменных технологических условиях - ничего, так как нежелание снизить цену своего товара или объема выпуска приведет к еще худшему результату. Таким образом, неценовые причины могут привести к переходу в новое состояние равновесия, и это свидетельствует о неустойчивости равновесия против неценовых возмущений в экономике.
. Что может противопоставить этому производитель? При данных неизменных технологических условиях - ничего, так как нежелание снизить цену своего товара или объема выпуска приведет к еще худшему результату. Таким образом, неценовые причины могут привести к переходу в новое состояние равновесия, и это свидетельствует о неустойчивости равновесия против неценовых возмущений в экономике.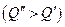 , что влечет повышение цены товара. Но до какого уровня? Если предложение подтягивается до нового уровня спроса, т.е. до величины
, что влечет повышение цены товара. Но до какого уровня? Если предложение подтягивается до нового уровня спроса, т.е. до величины  . Но такой цене соответствует спрос
. Но такой цене соответствует спрос 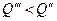 . Продолжая эти рассуждения, можно заметить, что цена последовательно приближается к равновесному значению
. Продолжая эти рассуждения, можно заметить, что цена последовательно приближается к равновесному значению 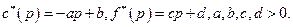
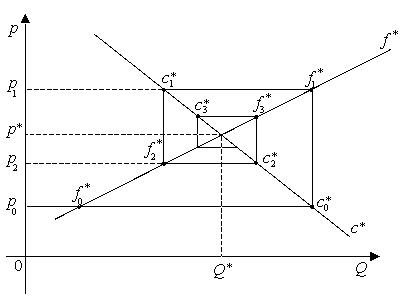
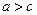 , т.е. наклон кривой спроса больше, чем наклон кривой предложения. Для отражения последовательного изменения значений, величины
, т.е. наклон кривой спроса больше, чем наклон кривой предложения. Для отражения последовательного изменения значений, величины 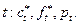 Моменты изменения их значений (моменты регулирования) обозначим через
Моменты изменения их значений (моменты регулирования) обозначим через 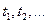 Для простоты положим
Для простоты положим 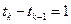 , т.е.
, т.е. 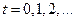 Пусть в начальный момент времени
Пусть в начальный момент времени 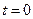 спрос
спрос  соответствует уровню цены
соответствует уровню цены 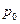 (см. Рис. 4.2) и превышает предложение, т.е.
(см. Рис. 4.2) и превышает предложение, т.е. 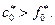 Предложение подтягивается к уровню
Предложение подтягивается к уровню 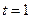
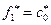 и соответствует уровню цены
и соответствует уровню цены  . Но этой цене в момент
. Но этой цене в момент  , который вынуждает цену уменьшиться до уровня
, который вынуждает цену уменьшиться до уровня  . Далее предложение снижается до уровня
. Далее предложение снижается до уровня 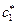 к моменту t=2
к моменту t=2 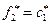 и т.д. Продолжая эти построения, мы приходим к общей закономерности:
и т.д. Продолжая эти построения, мы приходим к общей закономерности: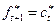 или
или 
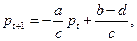
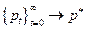 сходится для любых
сходится для любых 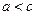 , т.е. наклон кривой спроса меньше, чем наклон кривой предложения, процедура расходится.
, т.е. наклон кривой спроса меньше, чем наклон кривой предложения, процедура расходится.