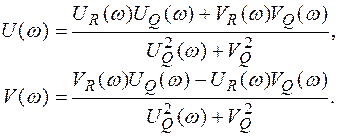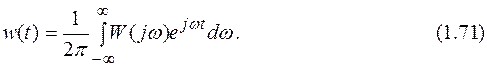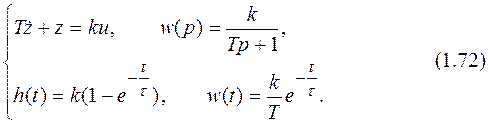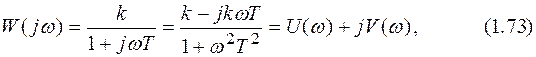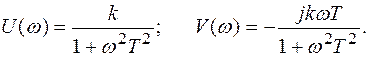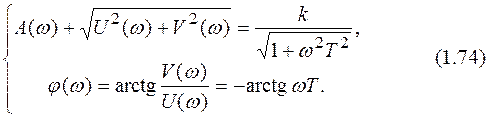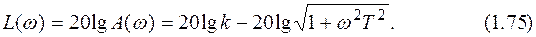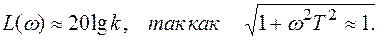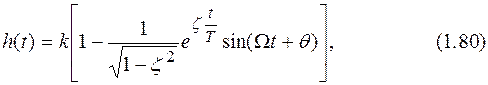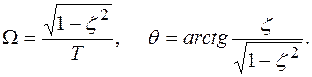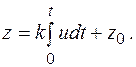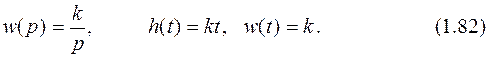|
|
Апериодическое (инерционное) звеноГЛАВА 1. ОПИСАНИЕ ОБЪЕКТА УПРАВЛЕНИЯ
Непрерывные модели
1.1.1. Построение модели простого объекта
Рассмотрим простейший объект - грузик, расположенный на горизонтальной плоскости и прикрепленный пружиной к вертикальной стенке. Между горизонтальной плоскостью и грузиком находится жидкая (или не очень) смазка (рис. 1).
Грузик первоначально находился в положении равновесия (его центр масс совпадал с координатой 0 по оси Х). Под действием внешней силы F грузик переместился на величину y. При этом пружина растянулась на эту же величину. В результате на грузик стала действовать возвратная сила пружины fпр, направленная в сторону, противоположную растяжению пружины. Кроме того, при движении грузика на него действует сила трения, направленная против направления его движения, и пропорциональная скорости движения. Грузик, как и любое физическое тело подчиняется второму закону Ньютона: где: m - масса грузика, a - ускорение движения грузика, x - результирующая сила, действующая на грузик.
Сила, обусловленная пружиной (предполагается, что она работает в пределах упругой деформации), пропорциональна жесткости пружины и деформации, и направлена в сторону, обратную деформации:
Сила жидкого трения, действующая на грузик, пропорциональна скорости его движения v и направлена против движения:
Здесь k – коэффициент трения. Результирующая сила, действующая на грузик, определяется алгебраической суммой всех сил – трения fтр, пружины fпр и внешней F.
Подставляя в (4) выражения (1) – (3), получаем:
Если учесть, что скорость и ускорение являются соответственно первой и второй производной от смещения
получаем окончательный вид уравнения движения грузика:
или
Результат ¾ обыкновенное линейное дифференциальное уравнение второго порядка. Обыкновенное дифференциальное уравнение получилось из-за того, что мы рассматривали абсолютно жесткий объект, который может быть заменен точкой массой m, а в пружине не учитывали конечной скорости распространения волны движения. Линейным уравнение получилось из-за того, что мы рассматриваем поведение пружины в пределах диапазона упругости. При нарушении указанных условий, дифференциальное уравнение может стать нелинейным, могут появиться частные производные и т. д. Таким образом, мы получили математическую модель объекта, изображенного на рис. 1, в виде дифференциального уравнения второго порядка. Получив решение этого уравнения, можно получить описание движения этого объекта, зависящее от начальных условий и от внешних воздействий. При решении дифференциальных уравнений удобнее иметь дело не с уравнениями высокого порядка (выше первого), а с системой уравнений первого порядка. Известно, что дифференциальное уравнение порядка n может быть преобразовано в систему из n уравнений первого порядка. Для преобразования получившегося уравнения второго порядка (9) заменим наблюдаемую переменную y на переменную состояния x1:
Тогда уравнение (9) примет следующий вид:
Если уравнение (11) проинтегрировать по времени, получим уравнение первого порядка
где
или иначе
В итоге получилось два уравнения первого порядка (12) и (14), дающие систему:
Полученная система дифференциальных уравнений первого порядка описывает динамику объекта, а уравнение (10) представляет собой уравнение наблюдения. В матричном виде эти уравнения имеют следующий вид:
Здесь буквами А, В и Н обозначены матрицы коэффициентов
х – вектор состояния, размерности 2, u – в данном случае, скалярное управление (в общем случае это тоже вектор), а y – в данном случае, также скалярное наблюдение (в общем случае – также вектор). Для решения системы уравнений (16) не хватает начальных условий, которые, конечно же, существуют, но не обязательно известны исследователю. Будем считать, что начальные условия известны, и они заданы в одной точке:
Уравнения (16) вместе с начальными условиями (18) дают, так называемую, задачу Коши:
характерной особенностью которой является задание системы дифференциальных уравнений в нормальной форме (разрешенных относительно первой производной) и заданием граничных (начальных) условий в одной точке. О решении этой задачи речь пойдет ниже. Здесь же надо сказать о том, что, рассмотрев объект, изображенный на рис. 1, мы смогли на основании общих физических соображений построить его математическую модель в достаточно общей форме. Контрольные вопросы к разделу 1.1.1 1. Что такое объект с точки зрения теории управления? 2. Что такое математическая модель? 3. Как построить математическую модель объекта? 4. Как перейти к системе дифференциальных уравнений первого порядка? 5. Как описать известные физические свойства объекта? 6. Что такое начальные условия? 7. Что такое задача Коши?
1.1.2. Непрерывная модель общего вида
В достаточно общем случае объект управления может быть описан дифференциальным уравнением вида:
или, учитывая общепринятое обозначение
где: х – вектор состояния, размерности n, u – вектор управления, размерности m, q – вектор параметров, размерности k, w – вектор случайных возмущений, размерности l, t – время, f – вектор-функция, размерности n. Одновременно с уравнением движения объекта (1.22) рассматривают уравнение наблюдения
где: z – вектор наблюдения размерности s, j - вектор-функция размерности s, v – вектор помехи измерения размерности р. Для большинства технологических объектов (различные промышленные печи, автоклавы, гальванические ванны и т. д.) и для многих движущихся объектов описание можно упростить. Для этих объектов характерны достаточно гладкие функции f и j, малые изменения вектора состояния, вектора управляющих воздействий и вектора возмущений относительно некоторых рабочих значений x, u, w, v, а также относительное постоянство параметров на рассматриваемых интервалах времени. В этих условиях описание объекта (1.22) и (1.23) можно заменить описанием движения объекта относительно этих рабочих значений – уравнениями в приращениях. Пусть переменные x, u, w и v в уравнениях (1.22) и (1.23) получили малые приращения, а вектор параметров постоянен:
Учитывая предполагаемую гладкость функций f и j, уравнения (1.24) можно разложить в ряд Тейлора относительно рабочей точки (x, u, w, v):
В формулах (1.25), (1.26) использованы обозначения: 0(×) – все остальные члены ряда (бесконечно малые относительно членов первого порядка малости),
Для упрощения записи введем обозначения:
Заменяя приращения переменных их прямым обозначением (в дальнейшем мы будем иметь дело только с приращениями), получаем компактную запись описания объекта:
Помеха измерения v в уравнении (1.28) не измеряется, а матрица F чаще всего неизвестна, поэтому второе слагаемое в этом уравнении обычно заменяют эквивалентной помехой
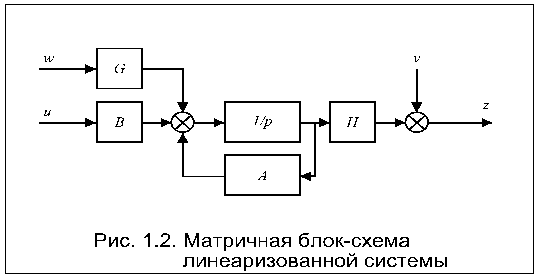
Систему уравнений (1.27), (1.29) можно представить в виде матричной блок-схемы (рис. 1.2).
Матрицы A, B, G, H в уравнениях (1.27) и (1.29) постоянны, если система стационарна (ее параметры не зависят от времени), или являются функциями времени, если система нестационарна. Пример. Имеется система:
Уравнения в приращениях линеаризованной системы согласно уравнениям (1.25), (1,26) будут иметь вид:
Не следует забывать, что все вычисленные выше производные берутся в точке разложения – рабочей точке.
Контрольные вопросы к разделу 1.1.2 1. Каково общее описание непрерывного объекта? 2. Какие параметры нужны для задания описания объекта? 3. Какие переменные входят в описание объекта? 4. В каком случае можно заменить общее описание объекта линейным? 5. Что такое уравнение в приращениях? 6. Что такое уравнение динамики? 7. Что такое уравнение наблюдения? 8. Что такое переменная состояния?
1.1.3. Нахождение траектории движения объекта
Рассмотрим систему, описываемую линейным дифференциальным уравнением
Здесь x – вектор размерности n, u – вектор размерности m, z – вектор наблюдений размерности k, A, B, H – матрицы коэффициентов размерности, соответственно, n ×n, n ×m, k ×n. Отметим, что первое уравнение в (1.30) определяет, так называемую, задачу Коши. Главным признаком задачи Коши является задание граничных условий на переменные в одной точке (не принципиально, в конце или в начале интервала). Если граничные условия для разных координат вектора состояния задаются в нескольких точках, то задача называется многоточечной граничной, или просто граничной. Важным случаем граничной задачи является двухточечная граничная задача (ДГЗ), которая возникает почти всегда при решении задач оптимизации, о чем еще будет разговор ниже. Для получения решения уравнения динамики объекта - первого уравнение в (1.30) – рассмотрим сначала однородное уравнение
Известно [4], что для уравнения (1.31) существует матрица Х(t,t0), которая называется фундаментальной матрицей системы (1.31) и является решением матричного дифференциального уравнения
где I – единичная матрица. Фундаментальная матрица Х(t,t0) обладает следующими свойствами [4,6]:
Свойство d) означает, что система, сопряженная с (1.31), имеет фундаментальную матрицу X(t0,t). Зная фундаментальную матрицу X(t,t0), можно записать решение уравнения (1.30):
Решение (1.36) называется решением в форме Коши. В решении (1.37) выделяют две составляющие – свободное движение (первое слагаемое) и вынужденное движение (второе слагаемое). Почему они так называются – достаточно очевидно: свободная составляющая присутствует только в том случае, если имеют место ненулевые начальные условия, и определяется она только начальными условиями и характеристиками системы (фундаментальной матрицей). Вынужденная составляющая присутствует только при наличии в системе внешних воздействий (в данном случае - вектора управления u), и определяется только внешними воздействиями и характеристиками системы (фундаментальной матрицей и матрицей В). Следует также отметить, что свободное движение никак не зависит от внешних воздействий, а вынужденная составляющая – от начальных условий. Выражение для выходной переменной z(t) имеет вид:
Если начальные условия нулевые (x(t0)=0), то выражение для выходной переменной примет вид:
или
где: W(t, t)=HTX(t, t)B(t) – весовая или импульсная переходная матрица размерности k ×m, W(t, t)={wij(t, t)}, wij(t, t) – реакция i-той выходной переменной в момент времени t на импульс (d-функцию), приложенный к j-тому входу в момент времени t. Если система (1.30) является стационарной, то есть, матрицы А, В, Н постоянны, то фундаментальная матрица становится функцией только одного аргумента
и может быть вычислена как экспоненциал матрицы
который определяется как степенной ряд [1,4]
В соответствии с (1.40) решение уравнения динамики стационарной системы имеет вид:
а для выходной переменной:
Весовая матрица W(t, t) в этом случае также является функцией одного аргумента
Применение к весовой матрице преобразования Лапласа дает передаточную матрицу
где: W(p)={wij(p)} – матрица передаточных функций, wij(p) – отношение изображения по Лапласу i-го выхода к изображению j-го входа при нулевых начальных условиях. Передаточную матрицу можно получить также, применяя преобразование Лапласа непосредственно к уравнению (1.30), считая начальные условия нулевыми
где x, u и z – изображения x(p), u(p) и z(p). Из первого уравнения (1.47) получаем:
Принимая во внимание второе уравнение в (1.47), получаем:
или
где W(p)=HT(Ip-A)-1B – передаточная матрица системы (1.30).
Пример. Пусть объект описывается системой уравнений:
Передаточная матрица определяется из выражений (1.50) и (1.51).
По найденной передаточной матрице можно записать дифференциальное уравнение для z.
Окончательно:
Это же уравнение можно получить из исходной системы дифференциальных уравнений.
Учитывая, что z=x1+2x2, получим:
что совпадает с ранее полученным уравнением.
Контрольные вопросы к разделу 1.1.3 1. Как решить задачу Коши? 2. Что такое фундаментальная матрица? 3. Решение в форме Коши. 4. Свободная составляющая движения. 5. Вынужденная составляющая движения. 6. Что такое весовая матрица? 7. Что такое передаточная матрица? 8. Что такое экспоненциал матрицы?
1.1.4. Переходные и частотные характеристики объекта
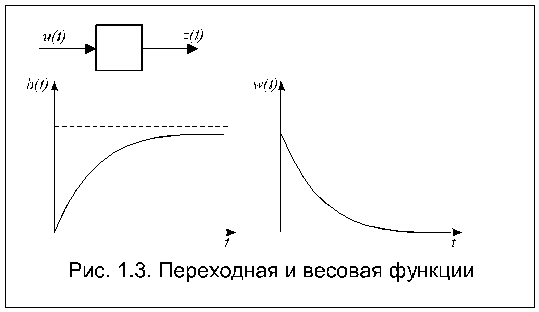
Часто для анализа систем автоматического управления используют разбиение всей системы на элементарные звенья. Под элементарным звеном обычно понимают часть системы управления не выше второго порядка, имеющую один вход и один выход. Динамические свойства элементарных звеньев могут описываться не только уравнениями и передаточными функциями, часто используют также переходные и частотные характеристики. Эти характеристики могут быть связаны экспериментально или построены по уравнению звена или по его передаточной функции. Возможно и обратное – по экспериментально построенным характеристикам составить уравнение звена или его передаточную функцию. Переходная характеристика (функция) представляет собой реакцию на выходе звена, вызванную подачей на его вход единичного ступенчатого воздействия. Единичное ступенчатое воздействие (единичная функция) – это воздействие, которое мгновенно возрастает от нуля до единицы и далее остается неизменным:
Кроме переходной функции применяется также весовая функция (импульсная переходная функция). Эта характеристика представляет собой реакцию звена на d-функцию (единичный импульс). d-функция (единичный импульс) – это импульс, площадь которого равна единице при длительности, равной нулю, и высоте, равной бесконечности:
Согласно определению d-функции справедливо:
Связь d-функции с единичной функцией достаточно проста (следует, конечно, иметь в виду, что соотношение символическое, так как производная от d-функции, строго говоря, не существует):
Из соотношения (1.55) следует аналогичная связь между переходной и весовой функциями:
Зная переходную или весовую функцию, можно определить реакцию звена на произвольное входное воздействие при нулевых начальных условиях:
Примерный вид переходной и весовой функций приведен на рис. 1.3.
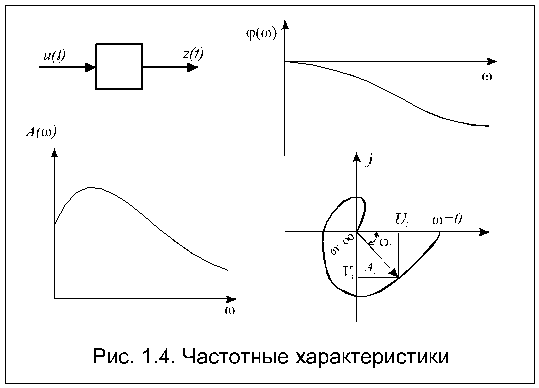
Частотные характеристики описывают установившиеся вынужденные колебания на выходе звена, вызванные гармоническим воздействием на входе. Если на вход звена подать гармонический сигнал
где umax – амплитуда сигнала, а wt – его угловая частота, то по окончании переходного процесса на выходе звена будет гармоническое колебание с той же частотой, что и входные колебания, но с другой амплитудой и фазой:
где zmax – установившаяся амплитуда выходного сигнала, а j – фазовый сдвиг между выходным и входным сигналом. Если на вход подавать сигнал с постоянной амплитудой и изменяющейся частотой, то изменение амплитуды и сдвига фазы выходного сигнала будут определяться динамическими свойствами звена. Если для различных частот, начиная с нулевой, измерить значения отношения амплитуд A=zmax/umax и сдвиг фаз j сигналов, получаются частотные характеристики звена: A(w) – амплитудно-частотная характеристика (АЧХ) и j(w) – фазо-частотная характеристика (ФЧХ). Примерный вид этих характеристик для простейшего звена представлен на рис. 1.4.
На рисунке показано, что в силу инерционности звена его частотная характеристика падает с ростом частоты (в пределе до нуля). Фазовая характеристика у обычных звеньев отрицательна (это значит, что выходной сигнал отстает от входного). При исследовании систем автоматического управления частотные характеристики удобнее рассматривать в логарифмических координатах. Во-первых, это позволяет удобно рассматривать достаточно большой диапазон частот, во-вторых, построение самих характеристик обычно упрощается. Кроме того, из определения амплитудных частотных характеристик непосредственно следует, что амплитудная частотная характеристика последовательно соединенных звеньев равна произведению амплитудных частотных характеристик отдельных звеньев [18]:
Если (1.59) прологарифмировать, получится:
Из соотношения (1.60) наглядно видно одно из преимуществ использования логарифмических частотных характеристик – вместо умножения характеристик последовательно соединенных звеньев надо складывать их логарифмы. То, что сложение проще, чем умножение, знают даже младшие школьники. Обычно используют амплитудную характеристику в виде зависимости 20lgA(lgw), называемой логарифмической амплитудно-частотной характеристикой (ЛАЧХ). Фазовую характеристику в виде зависимости j(lgw) называют логарифмической фазочастотной характеристикой (ЛФЧХ). Величина 20lgA обозначается L и измеряется в децибелах (1децибел = 0,1 бела). 1бел соответствует усилению сигнала по мощности в 10 раз, 2 бела – в 100 раз, 3 бела - в 1000 раз и т.д. Так как обычно измеряют не мощность сигнала, а его амплитуду, а мощность сигнала пропорциональна квадрату амплитуды, то усилению сигнала по мощности в 10 раз будет соответствовать lgA2=1 или 2lgA=1. Соответственно, усиление сигнала в децибелах, выраженное через отношение амплитуд равно 20lgА. При построении фазочастотной характеристики используют логарифмический масштаб по оси абсцисс и натуральный по оси ординат. Логарифмический масштаб по оси ординат не используют потому, что фазовый сдвиг при последовательном соединении звеньев итак складывается. Если на одних и тех же осях построить амплитудно-фазочастотную характеристику (АФЧХ), используя A(w) и j(w) в качестве полярных координат, то каждой точке этой характеристики в прямоугольной комплексной системе координат будут соответствовать действительная и мнимая часть вектора А. Частотные характеристики легко могут быть получены из передаточной функции звена. Запишем передаточную функцию звена в виде отношения полиномов от р (не будем забывать, что р=d/dt – оператор Лапласа):
Для удобства запишем входной и выходной гармонические сигналы в экспоненциальной форме:
Из (1.62) можно записать:
Подставим в уравнение (1.63) выражения для входной и выходной переменных (1.62), учитывая при этом, что
Так как слева и справа в (1.63) стоят суммы производных различного порядка, то, с учетом предыдущего замечания, получим:
Обозначим частотную характеристику звена через W(jw):
Учитывая, что umax/zmax = A, окончательно получаем:
Из соотношений (1.61) и (1.64) следует, что частотную характеристику можно получить из передаточной функции формальной заменой оператора Лапласа р на jw. Этот факт объясняется тем, что формулы преобразования Лапласа и преобразования Фурье имеют одинаковый вид. Если записать частотную характеристику W(jw) в алгебраической форме
где U(w) и V(w) представляют собой действительную и мнимую координаты частотной характеристики, показанные на рис. 1.4, можно связать алгебраическое представление частотной характеристики с представлением в полярных координатах:
Для вычисления частотных характеристик по передаточной функции достаточно подставить в передаточную функцию jw вместо р [18]:
Освободившись от мнимости в знаменателе, получаем:
В заключение осталось записать выражения, связывающие частотную характеристику с весовой функцией. Для этого запишем выражения аналогичные выражениям, связывающим передаточную функцию с весовой функцией, заменив преобразование Лапласа преобразованием Фурье:
Выражение (1.70) определяет частотную характеристику звена через его весовую функцию, а (1.71) – весовую функцию через частотную характеристику.
Контрольные вопросы к разделу 1.1.4 1. Что такое единичная функция? 2. Что такое дельта-функция? 3. Что такое весовая характеристика (функция)? 4. Что такое переходная характеристика (функция)? 5. Что такое частотная характеристика? 6. Как построить частотную характеристику? 7. Амплитудно-частотная характеристика. 8. Фазо-частотная характеристика. 9. Логарифмические частотные характеристики. 10. Как получить частотную характеристику из передаточной?
1.1.5. Типовые элементарные звенья
Апериодическое (инерционное) звено Дифференциальное уравнение этого звена, его передаточная, переходная и весовая функции имеют соответственно вид:
Примером апериодического звена может служить кирпич, положенный на конфорку кухонной плиты, если в качестве входа рассматривать, например, температуру конфорки, а в качестве выхода - температуру кирпича. Другим примером может служить двигатель постоянного тока, если в качестве входа рассматривать напряжение, поданное на двигатель, а в качестве выхода - скорость вращения якоря двигателя. Характеристики звена изображены на рис. 1.5.
Значение постоянной времени Т определяет инерционность звена: чем оно больше, тем дольше длится переходный процесс. Обычно считается, что переходный процесс завершается при достижении 0,95 от установившегося значения (теоретически экспоненциальный процесс не завершается никогда). Для апериодического звена длительность переходного процесса составляет примерно 3Т. Про частотные характеристики следует сказать более подробно. Частотная характеристика апериодического звена имеет вид:
где
Амплитудно-частотная и фазочастотная характеристики выражаются из алгебраического представления частотной характеристики (1.73):
Логарифмическая амплитудно-частотная характеристика получается из (1.74):
Логарифмические амплитудно-частотные характеристики звеньев обычно изображаются не в точном соответствии с (1.74) (на рис. 1.5. эта характеристика изображена кривой без излома), а в виде асимптотических характеристик (на рис. 1.5. асимптотическая характеристика изображена ломаной линией). Асимптоты определяются для малых значений частоты (w <<1/T) и для больших значений частоты (w >>1/T). При малых значениях частоты выражение (1.75) принимает вид:
То есть, для малых значений частоты характеристика представляет собой прямую, параллельную оси абсцисс на уровне 20 lg k. При больших частотах выражение (1.75) принимает другой вид:
То есть, для больших значений частоты характеристика представляет собой прямую, имеющую наклон – 20dB/dec. Обе асимптоты пересекаются в точке, соответствующей частоте w=1/T, называющейся частотой среза. Нетрудно определить, насколько асимптотическая характеристика отличается от истинной в точке, соответствующей частоте среза w=1/T:
Колебательное звено Дифференциальное уравнение звена имеет вид:
Параметры уравнения: Т – называется постоянной времени (1/Т = w0 – собственной частотой или частотой колебаний), z- коэффициентом затухания. Собственно колебательное звено имеет параметр z < 1. В этом случае характеристическое уравнение, соответствующее (1.76)
имеет комплексные корни:
При z ³ 1 в (1.78) получается два действительных корня, и колебательное звено превращается в апериодическое звено второго порядка (два апериодических звена первого порядка, соединенных последовательно). Передаточная функция колебательного звена, соответствующая дифференциальному уравнению (1.76), имеет вид:
Переходная функция, являющаяся решением уравнения (1.76) при единичном входном сигнале, имеет вид:
где: Из соотношений (1.80) видно, что коэффициент затухания z определяет форму огибающей, причем, чем меньше его значение, тем слабее затухание, а при равенстве его нулю, затухание отсутствует вовсе (незатухающие колебания). Частота колебаний W также зависит от z. Чем ближе значение z к единице, тем сильнее отличается W от w0. При z=0 частота колебаний совпадает с собственной частотой звена. Сдвиг фазы выходного сигнала относительно входного равен нулю при z=0, и стремится к бесконечности при приближении z к единице. Весовая функция получается дифференцированием выражения (1.80). Построение частотной характеристики производится так же, как и для апериодического звена. Отличие заключается в следующем: асимптотическая амплитудная характеристика имеет наклон после частоты среза не –20, а –40 дБ/дек, так как порядок звена равен двум, фазовая характеристика при увеличении частоты стремится не к –90о, а к –180о по той же причине, Вид характеристик колебательного звена показан на рис. 1.6. Типичным примером колебательного звена является грузик на пружинке, рассмотренный в начале главы.
Интегрирующее звено Это звено описывается уравнением
или в интегральной форме:
Передаточная, переходная и весовая функции звена
Примеры интегрирующего звена: – двигатель постоянного тока, где в качестве входа рассматривается напряжение, поданное на двигатель, а в качестве выхода – угол поворота ротора двигателя, – цилиндрический стакан, стоящий под струей воды, текущей из крана, где в качестве входа рассматривается угол поворота крана, а в качестве выхода – уровень воды в стакане. Следует отметить, что пример со стаканом, форма которого отлична от цилиндрической, не является интегрирующим звеном, так как объект становится нелинейным – приращение уровня воды в единицу времени зависит от самого уровня. Частотные характеристики интегрирующего звена строятся стандартным способом. Графическое представление характеристик интегрирующего звена представлено на рис. 1.7.
Дифференцирующее звено Это звено описывается уравнением
Передаточная и переходная функции дифференцирующего звена имеют вид:
Весовую функцию дифференцирующего звена трудно себе представить (производная от d-функции !), хотя при желании ее можно было бы описать. Частотные характеристики дифференцирующего звена строятся аналогично характеристикам для интегрирующего звена. Характеристики дифференцирующего звена в графическом виде представлены на рис. 1.8. На рисунке видно, что амплитудно-частотная характеристика растет с ростом частоты. Даже интуитивно понятно, что дифференцирующее звена в чистом виде (1.83) не существует, так как очень слабые высокочастотные наводки на входе звена должны были бы давать на выходе сигнал большой (вплоть до бесконечности) амплитуды. Реальные элементы, которые могут быть описаны дифференцирующим звеном, представляют собой как минимум последовательное соединение дифференцирующего и апериодического звена. При определенном ограничении рассматриваемой полосы частот объект можно описать дифференцирующим звеном. По мере увеличения частоты в реальном объекте проявляются апериодические звенья все более высокого порядка. примером дифференцирующего звена может служить тахогенератор постоянного тока (двигатель постоянного тока, якорь которого крутят, а с коллектора снимают генерируемое напряжение). Напряжение, измеряемое на коллекторе тахогенератора, пропорционально частоте вращения или производной от угла поворота. То есть, его можно описать дифференцирующим звеном, входом которого является угол поворота якоря, а выходом – измеряемое на коллекторе напряжение. При увеличении частоты входного сигнала в тахогенераторе начинает сказываться инерционность, обусловленная индуктивностью обмотки возбуждения. При дальнейшем увеличении частоты, начинает сказываться индуктивность обмотки якоря и т.д.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
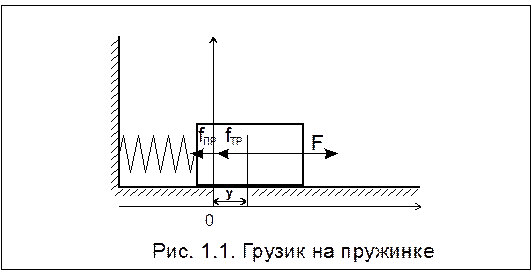





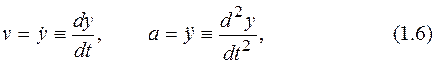











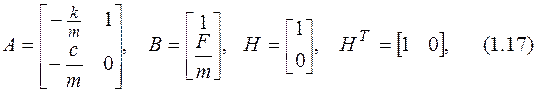

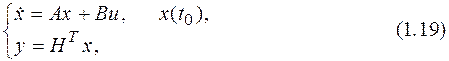






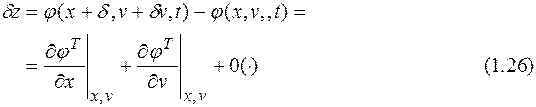
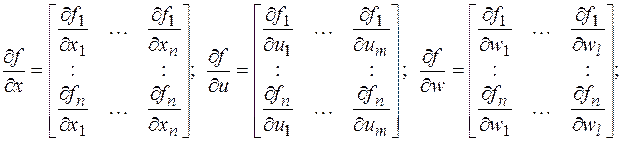






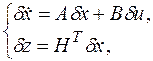



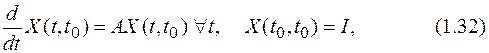


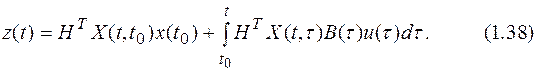
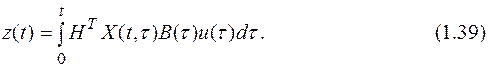



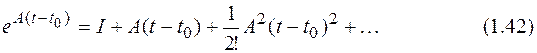
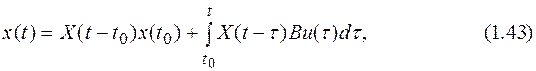
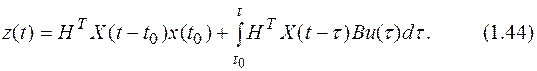
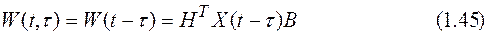





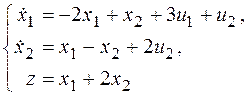
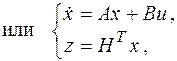

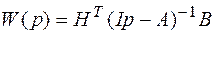
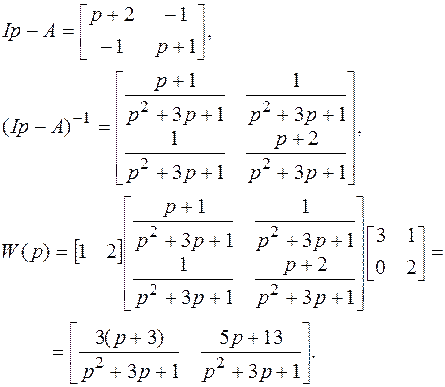
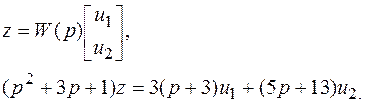

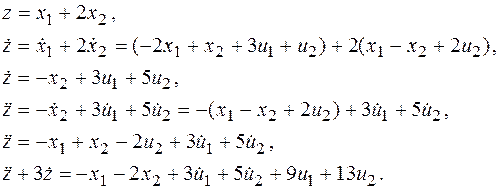
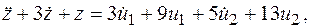
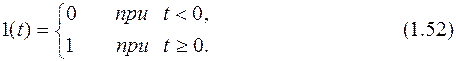
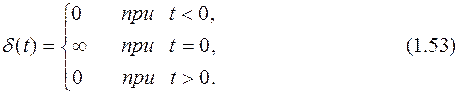





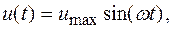

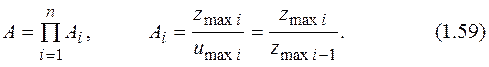

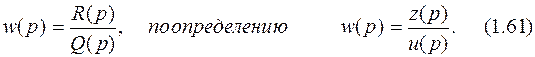
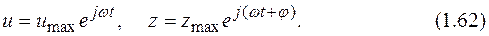

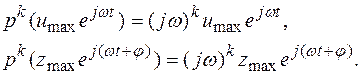
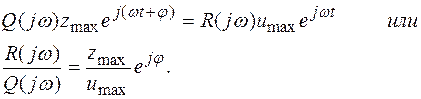



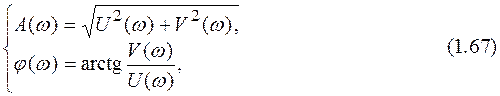


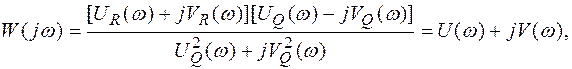 где:
где: