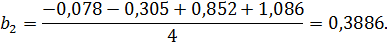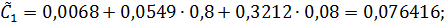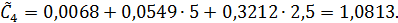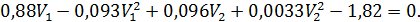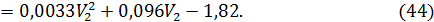|
|
Метод неопределенных множителей Лагранжа решения нелинейных задач оптимизации12
К классическим методам поиска экстремумов целевых функций относятся аналитические методы исследования функций с применением аппарата дифференциального исчисления. Как правило, эти методы позволяют найти лишь безусловные экстремумы. Для непрерывной функции F(xi, ..., xn), имеющей непрерывные производные первого и второго порядков, необходимым условием экстремума в точке пространства управляемых параметров
Решив систему уравнений, находят координаты всех стационарных точек целевой функции. Однако остается неясным вопрос о характере стационарной точки. Это может быть либо максимум, либо минимум, либо точка вовсе не является экстремальной, а лишь точкой перегиба. Теоретически достаточное условие максимума имеет вид:
а условие минимума –
В некоторых случаях характер стационарной точки ясен из физического смысла задачи. Аналитические методы исследования функций в общем случае не позволяют находить условные экстремумы. Но в случае ограничений-равенств задача условной оптимизации может быть сведена к задаче безусловной оптимизации методом неопределенных множителей Лагранжа. Заметим, что ограничения-равенства в задаче оптимизации означают, что область допустимых значений представляет собой границу той области, которая бы была задана неравенствами. Часто из анализа характера целевой функции становится ясно, что внутри области допустимых значений, задаваемой ограничениями-неравенствами, целевая функция не имеет локальных экстремумов и, следовательно, ее экстремальное значение будет находиться на границе этой области. Таким образом, во многих случаях, предварительный анализ характера целевой функции позволяет заменить ограничения-неравенства на ограничения-равенства в модели оптимизационной задачи. Если же целевая функция имеет экстремумы внутри области допустимых значений, то задача, по сути, является задачей безусловной оптимизации и может быть решена классическими методами исследования функций на максимум-минимум. Пусть в общем случае заданы целевая функция W(
Здесь величины λj, (j = 1, ..., m) называются неопределенными множителями Лагранжа и выступают как новые независимые переменные наравне с xi, (i = 1, ..., n). Взяв производные
и приравняв их к нулю, получим систему из n + m уравнений. Ее можно решить либо аналитически, либо численно. В точке условного экстремума
Расчет курсовой работы
Рассмотрим задачу моделирования и оптимизации процесса резания древесины. К процессам резания мы отнесем точение, сверление, пиление, фрезерование, шлифование и др. операции. Этот вопрос в течение длительного времени исследовался Ф.Р. Фергиным. Им было выведено эмпирическое уравнение для себестоимости обработки 1 погонного метра заготовки, которое имеет вид:
где V1 – скорость подачи заготовки (величина посылки), измеряемая в мм; V2 – стойкость режущего инструмента, км; A и B – коэффициенты, зависящие от затрат, соответственно первой и второй статьи. К первой статье затрат относятся затраты на оплату труда рабочих, техническое обслуживание станка, электроэнергию. Ко второй статье затрат относятся затраты на замену режущего инструмента, его переточку, здесь же учитываются простои станка в период смены инструмента. Коэффициенты А и В определяются методом математического моделирования по результатам экспериментов. Уравнение (32) может быть переписано в следующем виде:
где u1 = 1/V1, u2 = 1/(V1V2). Пусть допустимый диапазон параметров V1 и V2 определяется неравенствами:
тогда нетрудно установить, что диапазон изменения факторов u1 и u2 определяются неравенствами:
Значения u10 = (0,8 + 5)/2 = 2,9 и u20 = (0,08 + 2,5)/2 = 1,29 естественно принять за центр плана, а отклонения от этих значений до границ допустимого диапазона – за интервалы варьирования: δ1 = 2,1 и δ2 = 1,21. Совершив операцию приведения переменных по формуле (8), приходим от (33) к уравнению
Значения откликов С, полученных в результате эксперимента при варьировании х1 и х2 на двух уровнях, приведены в задании. Рассчитаем критерий Кокрена G по формуле (12) (наибольшая дисперсия в третьей строке)
Критическое значение критерия Кокрена, которое находим из приложения II, равно Gкр = 0,906 (n = 4, ƒ = 1, a = 0,05). Полученное значение G меньше критического и, следовательно, можно принять гипотезу однородности. То есть задача нахождения коэффициентов регрессии (36) при полученных значениях откликов поставлена корректно и мы можем приступить к ее решению. Рассчитаем усредненную оценку дисперсии воспроизводимости по формуле (14)
Дисперсия величин
Число степеней свободы (15) при этом составит
Теперь можно перейти к расчету коэффициентов регрессии по формуле (10). Поскольку коэффициент b0 определяется через фиктивную переменную x0 (x01 = x02 = x03 = x04 = 1), то
Аналогично рассчитываем b1 и b2:
Таким образом, получим
заменяя нормированные факторы x1 и x2 на u1 и u2 по формуле (9), получим Для проверки гипотезы о значимости коэффициентов регрессии рассчитаем дисперсию коэффициентов регрессии по формуле (17)
Из таблиц критерия Стьюдента (приложение II) находим t = 2,78 (ƒ = 4; а = 0,05), а затем доверительный интервал для коэффициента b1 (18):
Таким образом, коэффициенты регрессии, меньшие по абсолютной величине, чем 6,06·10–3 , можно считать незначимыми. Все коэффициенты уравнения значимы. Математическая модель останется в полученном виде:
Вычислим по этой формуле значение отклика для каждой строки матрицы планирования:
Остаточная дисперсия вычисляется для одной степени свободы (см. формулу (21): ƒ= n – p = 4 – 3 = 1) по формуле (20)
Критерий Фишера (22) равен
Критическое значение Fкр по уровню а = 0,05 (ƒ1 = 1, ƒ2 = 4) равно 7,71 (приложение II). Полученное значение критерия Фишера меньше критического, следовательно, уравнение адекватно. Таким образом, результатом математического моделирования явилось определение коэффициентов А = 0,0549 и B = 0,3212 в уравнении (32) для определения себестоимости С обработки 1 пог. м заготовки. При постановке задачи оптимизации параметров процесса резания древесины естественно принять себестоимость С в качестве целевой функции
Но при этом должны учитываться требования к качественным характеристикам продукции (технологически допустимый диапазон параметров процесса резания нами уже определен в виде неравенства (34)). В частности, в качестве требования к качественным характеристикам продукции мы можем наложить ограничение на величину разнотолщинности материалов обработки. Величина разнотолщинности материалов для процесса пиления древесины дисковыми пилами определяется по формуле
где t – толщина пил, мм; Q – постоянная, зависящая от высоты пропила, числа зубьев пилы, диаметра пилы, кинетического угла встречи. Примем t = 2,2 мм, Q = 11,4 и в качестве допустимого максимального значения разнотолщинности – Dmax = 2 мм. Тогда область допустимых значений будет определяться системой неравенств:
Графическая интерпретация задачи (39) представлена на рис. 1. (стрелкой g обозначено направление убывания целевой функции), в табл. 1 представлены данные для решения задачи.
Таблица 1 – Данные для решения задачи
Исходя из характера целевой функции C – монотонного убывания к верхней границе области допустимых решений, можно утверждать, что оптимум лежит на этой границе либо в вершинах 2 или 3 многоугольника 01234, либо в некоторой точке между ними на границе, описываемой уравнением (38) при D = Dmax . Нахождение значений целевой функции C и значений V1, V2 в точках 2 и 3 не представляет трудностей. Эти значения могут быть получены из решений соответствующих систем уравнений границ области допустимых решений.
Рисунок 1 – Графическая интерпретация задачи
Проанализируем решение в точке на границе (38). Координаты этой точки найдем, используя метод множителей Лагранжа.
Взяв частные производные по V1, V2, λ, получим
Исключая последовательно неизвестные λ, преобразуем эту систему уравнений к виду
где
Обозначения (43) и (44) введены для компактности записи системы (42). Эта система уравнений может быть решена численно-графическим способом. Так, из первого уравнения системы (42) рассчитываются значения V1, соответствующие заданным значениям V2, а из второго – значения функции Ф(V1, V2). Такие расчеты приведены в таблице 2.
Таблица 2 – Расчет значений V1 и Ф(V1, V2)
Затем строятся графики зависимостей Ф(V1) и Ф(V2), показанные на рисунке 2. Пересечение графика функции Ф(V1, V2) с осями V1 и V2 даст действительные корни уравнения Ф(V1, V2) = 0, а следовательно, и решение системы (42). Очевидно, что это решение и есть минимальное значение функции Лагранжа на границе (3.7). Из графиков рис. 2 находим V1 = 1,9 и V2 = 4,45. При этом C = 0,0688. Как видно из рис. 1, в точке с координатами V1 = 1,9 и V2 = 4,45 уровень целевой функции C = 0,0688 касателен к границе (3.7).
Рисунок 2 – Графики зависимостей Ф(V1) и Ф(V2)
Однако, полученное решение находится вне области допустимых решений задачи оптимизации, поскольку при использовании метода Лагранжа не учитывались ограничения на V1 и V2. Найденное значение V1 превышает верхний допустимый предел: V1 = 1,9 > 1,25. Анализируя значение целевой функции в ближайшей принадлежащей области допустимых решений точке 3, расположенной по границе (3.7), находим оптимальное решение: V1* = 1,25; V2* = 7,221; C = 0,079.
Заключение
В ходе курсовой работы была разработана математическая модель технологического процесса резания древесины, был проведен её анализ и оптимизация параметров процесса. При проверке гипотез о значимости коэффициентов регрессии и адекватности полученного уравнения исследуемого процесса было выявлено три значимых коэффициента регрессии и получено адекватное уравнение исследуемого процесса, что позволило сформулировать математическую модель задачи оптимизации параметров процесса резания. Задача была решена графическим методом, проанализировав который можно выявить возможное положение экстремума, который находится в точке касания графика С = 0,0688 с графиком ограничения по величине разнотолщинности материалов для процесса пиления древесины дисковыми пилами. Координаты этого экстремума были определены методом множителей Лагранжа: V1 = 1,9 и V2 = 4,45. Однако, данный экстремум не входит в область допустимых решений задачи оптимизации, поэтому в качестве оптимального решения данной задачи была выбрана точка с координатами V1* = 1,25; V2* = 7,221, находящаяся в вершине 3 области допустимых решений, для которой целевая функция равна C = 0,079.
Библиографический список
1. Моделирование и оптимизация процессов в деревообработке [Текст]: методические указания к курсовой работе/ – Воронеж: ФГБОУ ВО «ВГЛТУ», 2015 – 34 с. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 служит равенство нулю в этой точке частных производных по всем переменным. Другими словами, для поиска экстремума берут частные производные от целевой функции по всем переменным, и полученные уравнения приравнивают к нулю:
служит равенство нулю в этой точке частных производных по всем переменным. Другими словами, для поиска экстремума берут частные производные от целевой функции по всем переменным, и полученные уравнения приравнивают к нулю:

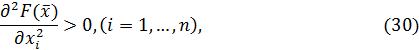


 будем иметь G(
будем иметь G(  ) = W(
) = W( 


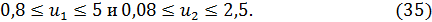



 j, вычисляемая по (16), составит
j, вычисляемая по (16), составит