
|
|
Построение математических моделей процессов методом наименьших квадратов по экспериментальным данным12 Задание
Вариант 9
Реферат
Курсовая работа заключается в разработке математической модели технологического процесса резания древесины, ее анализе и оптимизации параметров процесса. Курсовая работа включает выполнение следующих видов работ: 1) разработку математической модели технологического процесса резания древесины в виде линейного, относительно коэффициентов, уравнения регрессии методом наименьших квадратов; 2) проверку гипотез о значимости коэффициентов регрессии и адекватности полученного уравнения исследуемому процессу; 3) формулировку математической модели (целевой функции и ограничений) задачи оптимизации параметров процесса резания древесины; 4) графический анализ характера целевой функции и области допустимых решений оптимизационной задачи с целью определения возможного положения экстремума; 5) формулировку, на основе проведенного графического анализа, задачи безусловной оптимизации путем введения новой целевой функции с неопределенными множителями Лагранжа; 6) решение задачи оптимизации параметров технологического процесса резания древесины методом множителей Лагранжа; 7) анализ полученного решения и формулировку выводов о проделанной работе. Пояснительная записка содержит: 28 листов; 2 рисунка; 2 таблицы; 44 формулы.
Содержание
Введение. 5 1 Построение математических моделей процессов методом наименьших квадратов по экспериментальным данным. 6 2 Методика планирования эксперимента для построения математических моделей в виде линейных уравнений регрессии. 9 3 Методика проверки гипотез в планированном эксперименте. 12 4 Математическая формулировка оптимизационных задач. 15 5 Метод неопределенных множителей Лагранжа решения нелинейных задач оптимизации 18 6 Расчет курсовой работы.. 20 Заключение. 28 Библиографический список. 29
Введение
На современном этапе развития производства, особенно в условиях реформирования экономики, всестороннее повышение качества управления производством, его технологическими объектами является определяющим фактором жизнеспособности предприятий. Деревообрабатывающие производства насыщаются в настоящее время автоматизированными системами различных уровней, функционирующими на базе современных средств вычислительной техники. Автоматизация осуществляется на основе математических методов моделирования и оптимизации производственных и технологических процессов, успешному внедрению которых способствует применение ЭВМ. Использование методов моделирования и оптимизации позволяет выполнять многовариантный анализ решений при проектировании и управлении технологическим процессом и выбирать наилучшее по тем или иным критериям. Это значительно повышает качество и эффективность управления производством, позволяет оптимально организовать технологический процесс, обеспечить наилучшее использование сырья, энергоресурсов и рабочей силы, сделать процесс гибким, способным оперативно адаптироваться к изменяющимися условиям производства. Поэтому современный специалист деревообрабатывающей отрасли должен обладать знаниями методов моделирования и оптимизации и уметь их применять на практике. Выпускник факультета технологии деревообработки для этого должен научиться разрабатывать математические модели технологических процессов деревообработки, проводить их анализ, ставить и решать задачи оптимизации этих процессов. Для приобретения таких навыков студенты выполняют курсовую работу.
Построение математических моделей процессов методом наименьших квадратов по экспериментальным данным
Метод наименьших квадратов играет важную роль при решении обратных задач моделирования, то есть задач определения неизвестных параметров (коэффициентов) b0, b1, ..., bp в математическом описании заданного вида некоторого процесса
где (x1, x2, ..., xk) – вектор контролируемых факторов, y – отклик. Задача состоит в том, чтобы по опытным данным наилучшим образом определить значения параметров b математической модели. Примем, что опытные значения факторов x задавались точно, но значения отклика y получались со случайными ошибками. Метод наименьших квадратов сводится к следующему: наилучшими будут те значения параметров b, при которых сумма квадратов отклонений, рассчитанных по модели величин ỹ, от опытных y окажется наименьшей. Запишем условия совокупности n опытов по определению отклика y в виде матрицы плана эксперимента
Здесь каждая строка – условия одного опыта; каждый столбец – значения одного фактора в разных опытах; xij – значение i-го фактора в j-м опыте. Рассмотрим также вектор-столбец результатов эксперимента
Приведенное выше определение метода наименьших квадратов может быть записана в виде формулы:
где ỹj – расчетное значение отклика для j-той строки матрицы Те значения b, при которых S окажется минимальной, и будут наилучшими. Проще всего расчет методом наименьших квадратов осуществляется, когда уравнение (1) линейно относительно коэффициентов b. В этом случае функцию (1) можно записать в виде:
где xi – известные заранее значения контролируемых факторов. В формулу (5) для симметрии введена величина x0i , она всегда равна 1, то есть b0x0 = b0. Поэтому x0 называют фиктивной переменной. Для рассматриваемого случая матрица
Решение уравнения (4) в матричных обозначениях имеет вид:
где верхний индекс T обозначает транспонирование матрицы, а верхний индекс -1 есть символ обращения матрицы;
Для нахождения коэффициентов b по формуле (7) необходимо, чтобы число опытных точек n было не меньше числа рассчитываемых параметров. Иначе число степеней свободы, равное разности между числом точек и числом параметров, окажется отрицательным, а расчет невозможным. Матрица
2 Методика планирования эксперимента для построения математических моделей в виде линейных уравнений регрессии
Идея планирования эксперимента – предусмотреть изменение всех влияющих факторов в опытах так, чтобы обеспечить максимум точности и минимум корреляции. Для построения математических моделей в виде полиномов 1-й степени (линейных уравнений регрессии) служат многофакторные ортогональные планы 1-го порядка. Наиболее распространен следующий порядок построения планов. Выбирается центр исследуемой области (центр плана), то есть значения регулируемых факторов ui0 в центре факторного пространства. В центр плана переносится начало координат. Затем выбирается интервал варьирования по каждому фактору δi – расстояние по данной оси в факторном пространстве до экспериментальной точки. Выбор центра плана и интервала варьирования лежит вне математической теории. Этот этап задачи решается экспериментатором на основе знания исследуемых процессов. В последующих экспериментах наибольшее значение каждого из факторов (верхний уровень) равно ui0 + δi, а наименьшее (нижний уровень) равно ui0 – δi. Оптимальными свойствами обладают планы 1-го порядка, в которых каждый фактор принимает лишь два значения – варьируется на двух уровнях, верхнем и нижнем. На следующем этапе совершают операцию приведения (кодирования) переменных. Она заключается в том, что все координаты центра плана приравниваются нулю, а интервалы варьирования принимаются за 1. Переход от натуральных значений переменных ui к кодированным xi и обратно производится по формулам:
и соответственно
Если ui – на нижнем уровне, то xi = -1; если ui – на верхнем, то xi = +1 (в центре плана xi = 0). Для двух факторов x1 и x2 в приведенных координатах матрица планирования имеет вид:
-1 0 1 x1
-1
Рассмотренный план построен так, что каждый фактор варьируется на двух уровнях, причем в опытах перебираются все возможные комбинации двух уровней факторов. Такой план называют планом полного факторного эксперимента (ПФЭ) на двух уровнях. Нетрудно показать, что все недиагональные элементы
где k – число факторов. Простота расчета коэффициентов b методом наименьших квадратов для ПФЭ на двух уровнях обусловлена ортогональностью матрицы планирования. Это означает, что все векторы (столбцы матрицы) удовлетворяют соотношению:
Сам план также называют ортогональным. Простота расчета для ортогонального плана является заметным преимуществом, но не очень существенным в связи с широким применением ЭВМ. Важно следующее: ортогональность двух столбцов означает полное отсутствие корреляции соответствующих факторов. Следовательно, и оценки параметров оказываются некоррелированными. Некоррелированность позволяет легко проверить гипотезу о значимости факторов, а если какой-либо член окажется незначимым, то он просто исключается из уравнения, и это никак не сказывается на величине остальных параметров.
3 Методика проверки гипотез в планированном эксперименте
Интерпретация результатов эксперимента обычно проводится в терминах проверки гипотез. Обычно проверяются следующие гипотезы: 1) об однородности оценок дисперсий, полученных для разных строк матрицы планирования; 2) о значимости коэффициентов регрессии; 3) об адекватности уравнения. Однородность оценок дисперсий проверяют потому, что могут быть случаи, когда в разных частях пространства факторов точность опытов разная. В случае неоднородных дисперсий вся дальнейшая обработка окажется некорректной. Для возможности проверки гипотезы однородности оценок дисперсий предусматривается проведение параллельных опытов, то есть получение в каждой точке плана эксперимента нескольких значений откликов. Для сравнения ряда дисперсий известно несколько критериев. Наиболее прост критерий Кокрена G. Однако пользоваться им можно, только если все дисперсии S2j рассчитаны по одному и тому же числу степеней свободы, то есть количество параллельных опытов для каждой строки матрицы эксперимента должно быть одинаковым. Критерий равен отношению наибольшей из дисперсий к сумме их всех;
где дисперсии S2j определяется по формуле
где m – число параллельных опытов в серии, n – число серий. Критическое значение Gкр зависит от числа степеней свободы ƒ при оценке каждой из S2j (ƒ = m – 1), от числа дисперсий n и от уровня значимости а (а ~ 0,01 ÷ 0,1). Если G < Gкр, то гипотеза однородности с выбранным уровнем значимости а принимается. Если дисперсии однородны, дисперсия воспроизводимости находится усреднением:
а число степеней свободы при этом составит
При дальнейшей обработке, например, расчете коэффициентов по формуле (10), целесообразно подставить в формулу (10) и в другие расчетные формулы в качестве yj средние арифметические
Гипотеза о значимости коэффициентов регрессии проверяется следующим образом. Рассчитывают дисперсию коэффициента регрессии. Для факторных планов на двух уровнях она равна
Затем находят доверительный интервал для коэффициента – тот интервал, в пределах которого коэффициент, в действительности равный нулю, может отклониться от истинного значения с данной малой вероятностью. Доверительный интервал dbi составляет
где t находят по таблицам критерия Стьюдента для выбранного уровня значимости. Если для какого-либо коэффициента окажется, что
то данный член можно считать незначимым и исключить из уравнения регрессии. Гипотезу адекватности проверяют следующим образом. Для каждой j-й строки матрицы плана вычисляют расчетное значение ỹj. Предварительно из уравнения регрессии вычеркивают незначимые члены. Затем находят остаточную дисперсию
где
n – число строк матрицы плана; p – число значимых коэффициентов регрессии. Проверку адекватности проводят по критерию Фишера
Уравнение адекватно, если F < Fкр, где Fкр находят по таблицам критерия Фишера для выбранного уровня значимости в зависимости от количества степеней свободы числителя (21) и знаменателя (15). При неадекватности уравнения переходят к более сложной модели.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|




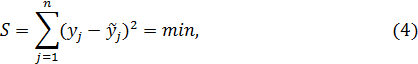
 .
.


 – вектор искомых параметров b.
– вектор искомых параметров b. в уравнении (7) – квадратная. Это значит, что если определитель этой матрицы не равен нулю, то имеется единственное решение уравнения (7), т.е. единственный набор коэффициентов. В случае, когда этот определитель равен нулю, матрица вырождена, и система имеет бесконечно много решений, тогда по данным опытным точкам нельзя однозначно определить параметры модели. Вырождение матрицы связано с взаимной корреляцией факторов. Исключения корреляции факторов добиваются специальным выбором опытных точек, что реализовано в ортогональных планах экспериментов.
в уравнении (7) – квадратная. Это значит, что если определитель этой матрицы не равен нулю, то имеется единственное решение уравнения (7), т.е. единственный набор коэффициентов. В случае, когда этот определитель равен нулю, матрица вырождена, и система имеет бесконечно много решений, тогда по данным опытным точкам нельзя однозначно определить параметры модели. Вырождение матрицы связано с взаимной корреляцией факторов. Исключения корреляции факторов добиваются специальным выбором опытных точек, что реализовано в ортогональных планах экспериментов.










 x2
x2





 , полученные в каждой строке. Тогда дисперсия величин
, полученные в каждой строке. Тогда дисперсия величин 





