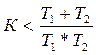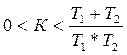|
|
Структурные схемы систем управления
Условные обозначения Система управления разбивается на блоки, имеющие вход и выход: объект, регулятор, привод, измерительная система. Для того, чтобы показать взаимосвязи этих блоков используют структурные схемы. На них каждый элемент изображается в виде прямоугольника, внутри которого записывается его передаточная функция. Вход и выход блока показывают соответственно входящей и выходящей стрелками.
  Х - вход Y- выход Х - вход Y- выход
Еще в структурных схемах используются суммирующие элементы (сумматоры - представляют собой круг, разбитый на 4 сектора) для суммирования (вычитания) сигналов и точки разветвления сигналов.
(-) Х Х3
Правила преобразования Многие методы исследования систем управления основаны на использовании передаточных функций. для построении передаточной функции системы в целом или передаточной функции между любым входом и выходом системы необходимо преобразовать структурную схему так, чтобы в итоге остался всего один блок с известной передаточной функцией. Для этого используют правила преобразования структурных схем. Передаточные функции параллельного и последовательного соединения равны соответственно сумме и произведению исходных передаточных функций:
Для последовательного соединения:
Y(s) = W2(s) Y1(s) = W2(s) W1(s) X(s)
Для параллельного соединения:
Y(s) = Y1(s) + Y2(s) = W1(s) X(s) + W2(s) X(s) = [W1(s) + W2(s)] X(s)
Соединения с обратной связью: положительная обратная связь
 Х е Y X Y Х е Y X Y
f
отрицательная обратная связь
 X e Y X Y X e Y X Y
f (-)
Доказательство: Y(s) = W1(s) E(s) ; E(s) = X(s) ± F(s) = X(s) ± W2(s) Y(s)
Y(s) = W1(s) [X(s) ± W2(s) Y(s)] ; Y(s)[1
Звено можно переносить через сумматор как вперед, так и назад. Чтобы при этом передаточные функции не изменились, перед сумматором необходимо поставить дополнительное звено:
f
X Y <=> X Y
f
 f f
<=>
 
Звено можно также переносить через точку разветвления, сохраняя при этом передаточную функцию:
  <=> X Y1 <=> X Y1
Y2
 Y2 Y2
Типовая одноконтурная система Для указанного ниже примера применим приемы вычисления и преобразования передаточных функций:
 Х e u d y Х e u d y
(-) g
m
В представленной системе три входа: X (вход системы), g (возмущение), m (шум измерений); и три выхода: y (выход системы), u (сигнал управления), e (ошибка регулирования). Таким образом, всего можно записать девять передаточных функций, соединяющие все возможные пары вход-выход. Кроме того, на схеме обозначены: d - управляющее воздействие на объект управления; C(s) - регулятор; R(s) - привод; P(s) - объект управления; H(s) - измерительная система (датчик (-и)). Найдем передаточные функции от входа Х ко всем выходам, для этого все остальные входы будем считать нулевыми и удалим их со схемы:
 X Y X Y
(-)
Принимая в качестве выходов управление u и ошибку е, получим такие схемы и передаточные функции:
Передаточная функция по управлению u от входа Х равна Wu(s):
 X е u X е u
(-)
Передаточная функция по ошибке е от входа Х равна We(s):
(-)
Используя этот подход, легко найти передаточные функции для других входов.
Анализ систем управления При управлении системами ставятся следующие цели: · точность – в установившемся режиме система должна поддерживать заданное значение входа, причем ошибка (разница между заданным и фактическим значением) не должна превышать допустимую величину; · устойчивость – система должна оставаться устойчивой во всех режимах; · качество переходных процессов - при смене заданного значения система должна переходить в нужное состояние по возможности быстро и плавно; · робастность – система должна сохранять устойчивость и приемлимое качество даже в том случае, если динамика объекта и свойства внешних возмущений отличаются от используемых при проектировании. 4.1. Точность Точность системы обычно оценивается для одного из эталонных сигналов: Единичный скачок
Линейно-возрастающий сигнал
Гармонический сигнал
Точность системы в установившемся режиме определяется ошибкой e(t) или ее изображением E(s). Для исследования точности используют передаточную функцию по ошибке We(s), которая связывает изображения ошибки и входного сигнала:
регулятор объект
(-)
E(s) = We(s) * X(s) Разложим функцию We(s) в ряд, получим:
где: Представим передаточные функции C(s) и P(s), изображение входа X(s) в виде отношения полиномов:
С учетом этого передаточная функция по ошибке из представленной схемы равна:
где: Δ(s) = dc(s) d(s) + nc(s) n(s) – характеристический полином замкнутой системы. Рассмотрим реакцию системы на единичный ступенчатый сигнал, изображение которого равно: Сигнал ошибки определяется полюсами передаточной функции We(s) (корнями Δ(s) и полюсами изображения X(s)). Все полюса We(s) должны иметь отрицательные вещественные части (иначе система будет неустойчивой), нулевых полюсов у функции We(s) тоже нет. Тогда [1]:
где: Y0(s) – полюса только с отрицательной вещественной частью;
Для того чтобы сделать нулевую ошибку достаточно обеспечить: dc(0) = 0 регулятор содержит интегратор; d(0) = 0 объект содержит интегратор. Таким образом, для любых незатухающих входных сигналов ошибка стремится к нулю в том случае, если их полюса сократились в произведении:
Это возможно только тогда, когда они являются корнями полинома dc(s)d(s). Например, для точного отслеживания ступенчатого сигнала нужно, чтобы объект или регулятор содержали интегрирующее звено (с передаточной функцией 1/s). Тогда произведение dc(s)d(s) имеет сомножитель s и полюс X(s) в точке s=0 сократится в произведении We(s) X(s). Таким образом, если передаточная функция разомкнутого контура C(s)P(s) содержит множитель s в знаменателе, обеспечивается нулевая ошибка слежения за постоянным сигналом (нулевая статическая ошибка). Такая система называется астатической. Для отслеживания линейно возрастающего сигнала в таком контуре должно уже быть два интегратора (нужно сократить двойной полюс X(s) в точке s=0). Такая система обладает астатизмом 2-го порядка. В общем случае система, в которой:
где: ν > 0 натуральное число; функция G(s) не имеет нулей и полюсов в точке s=0; называется астатической системой ν-го порядка. Такая система в установившемся режиме без ошибки отслеживает сигнал вида:
Казалось бы, для повышения точности системы можно поставить множество интеграторов и проблемы воспроизведения без ошибки входного сигнала любого вида будут решены. Однако добавление каждого нового интегратора в систему ухудшает качество переходных процессов, осложняет стабилизацию системы, снижает ее быстродействие.
4.2. Повышение точности систем управления Известны следующие общие методы повышения точности систем [1]: 1. Увеличение коэффициента передачи разомкнутой системы. 2. Повышение порядка астатизма. 3. Управление производными по ошибке Первый метод является наиболее универсальным и эффективным: как результат его применения является уменьшение ошибок практически во всех режимах. Однако увеличение коэффициента передачи ограничивается устойчивостью системы. При повышении коэффициента передачи переходные процессы в системе приобретают колебательный характер, при предельном значении возникают незатухающие колебания. На практике повышение коэффициента передачи обычно производится только при повышении запаса устойчивости системы, что осуществляется при помощи корректирующих средств (звеньев). Второй метод используется для устранения установившихся ошибок в различных типовых режимах (введением интегрирующих звеньев) [1]:
 g x y g x y
Пример
Характеристический полином замкнутой системы равен: Т1Т2s4 + (Т1+Т2)s3 + s2 + К*Ки
Как видно, при s слагаемое в полиноме отсутствует (т.е. а3 = 0), значит, система структурно неустойчива, необходимо изменить структуру системы только при помощи корректирующих средств.
Кроме интегрирующих звеньев в этом методе используется введение изодромных устройств.
Вернемся к предыдущему примеру. Передаточная функция разомкнутой системы в случае введения изодромного звена равна:
Характеристический полином замкнутой системы равен: Т1Т2s4 + (Т1+Т2)s3 + s2 + К*КиТиs + К*Ки Коэффициенты ошибок равны: с0 = с1 = 0
Третий метод повышения точности – управление производными по ошибке – заключается в ведении дифференцирующего элемента:
Введение дифференцирующего элемента не влияет на первый, отличный от нуля, коэффициент ошибки, но зато уменьшает последующие коэффициенты [1]. На практике наиболее эффективное снижение ошибки в системе заключается в одновременном использовании изодромных (не более трех) и дифференцирующих (не более двух) элементов. 4.3. Анализ устойчивости линейных непрерывных систем управления Понятие устойчивости является особенно важным, поскольку данное свойство системы определяет факт ее работоспособности или неработоспособности. Линейные системы управления обладают особенностями, которые во многих случаях упрощают анализ устойчивости: · устойчивость - это свойство линейной системы, а не отдельного положения равновесия: или все движения системы устойчивы, или все движения неустойчивы; · устойчивость линейной системы не зависит от вида и характера изменения задающего и возмущающих воздействий. Для того, чтобы получить условия устойчивости рассмотрим уравнение движения линейной системы, на которую не действуют возмущения. передаточная функция системы имеет следующий вид:
где: n(s), Δ (s) - полиномы; αi (i=1,...n) - простые (некратные) полюса (корни знаменателя). Из теории дифференциальных уравнений известно, что при отсутствии возмущений выход такой системы можно представить в виде:
где: αi (i=1,...n) - постоянные, определяющиеся начальными условиями. Процесс y(t) затухает при любых начальных условиях тогда и только тогда, когда все корни αi имеют отрицательные вещественные части. В этом случае система асимптотически устойчива [1]. Таким образом, устойчивость линейной системы управления определяют корни полинома Δ (s) - знаменателя передаточной функции. Этот полином называется характеристическим полиномом системы. Так как все коэффициенты полинома Δ (s) вещественные, комплексные корни всегда будут парными. Если один из корней αi полинома Δ (s) равен нулю, а остальные корни устойчивы, это значит, что система содержит интегрирующее звено:
здесь все слагаемые затухают с течением времени, а постоянная составляющая αi остается, в этом случае система нейтрально устойчива. Если характеристический полином имеет пару чисто мнимых корней: α1= jω α2= - jω, то система содержит консервативное звено (генератор колебаний). На выходе получится:
Эти составляющие дают незатухающие колебания, система в этом случае нейтрально устойчива. Если в характеристическом полиноме имеется хотя бы один корень с положительной вещественной частью, то система неустойчива. Критерии устойчивости На практике обычно пользуются критериями устойчивости - правилами, позволяющими оценить устойчивость без вычисления корней. Критерии устойчивости классифицируют на алгебраические и частотные. Алгебраические критерии позволяют определить устойчивость системы при помощи только алгебраических процедур над коэффициентами характеристического уравнения. К ним относятся критерии устойчивости Рауса, Гурвица и другие. Частотный критерий устойчивости, впервые сформулированный Найквистом, был применен для устойчивости систем управления А.В. Михайловым. Кроме того, последний сформулировал другой частотный критерий, названный его именем. Достоинством частотных критериев является их наглядность, а также возможность использовать частотные характеристики, полученные экспериментально, когда неизвестны дифференциальные уравнения системы или его элементов. Наибольшее распространение получил алгебраический критерий устойчивости, сформулированный Гурвицем. Для характеристического полинома (уравнения) системы:
составим квадратную матрицу Hn, содержащую n строк и n столбцов.
Первая строка содержит коэффициенты с нечетными номерами (a1,a3,a5,....) - оставшиеся элементы матрицы заполняются нулями. Вторая строка содержит коэффициенты с четными номерами (a0,a2,a4,....) - оставшиеся элементы матрицы заполняются нулями. Третья и четвертая строки получаются сдвигом первой и второй строк на одну позицию вправо и т.д. Например, для системы пятого порядка такая матрица H5 имеет вид:
Критерий Гурвица: все корни полинома Δ (s) имеют отрицательные вещественные части тогда и только тогда, когда все n главных миноров матрицы Hn (определителей Гурвица) положительны: Δ n = an Δn-1 > 0. Система находится на границе устойчивости, когда Δ n = 0: при an =0 - апериодическая граница устойчивости; при Δn-1=0 - колебательная граница устойчивости. Определители Гурвица составляются по следующему правилу:
Δ1 = a1 > 0
Δ2 = Δ3 = Раскрывая определители, фигурирующие в общей формулировке критерия, можно получить в виде частных случаев критерии устойчивости для систем: 1-го, 2-го, 3-го и более высоких порядков. Для систем 1-го порядка: a0 s + a1 ; a0 >0 Δ1 = a1 > 0 Для систем 2-го порядка: a0 s2 +a1 s + a2 ; a0 >0 Δ1 = a1 > 0 Δ2 = a1a2 > 0 a2 > 0 Для систем 3-го порядка: a0 s3 +a1 s2 + a2 s +a3 ; a0 > 0 a1 > 0 a2 > 0
Δ3 = a3
a1 a2 - a3 a0 >0 a1 a2 > a3 a0
Как видно, помимо положительности всех коэффициентов характеристического полинома с ростом порядка системы возникают другие условия. Как правило, использование критерия Гурвица ограничивается уравнениями четвертого порядка. Критерий Гурвица не дает для высоких порядков характеристического уравнения ответа на вопрос, каким образом надо изменять параметры системы, чтобы она была устойчивой. Пример
регулятор объект
(-)
При каких значениях К система будет устойчивой по критерию Гурвица?
Δ(s) = Т1Т2s3 + (Т1+Т2)s2 + s + К
Условия устойчивости: К > 0 ; Т1*Т2 > 0 ; Т1+Т2 > 0
(Т1+Т2) * 1 > К * Т1Т2 Отсюда:
С учетом того, что постоянные времени Т1 и Т2 всегда больше нуля, система устойчива при следующих значениях К:
Критерий Найквиста Это графоаналитический критерий, в котором вывод об устойчивости или неустойчивости замкнутой системы делается в зависимости от вида частотной характеристики разомкнутой системы. Кроме того, при помощи этого критерия можно оценить качественные показатели замкнутой системы (например, запас устойчивости). Критерий Найквиста позволяет определить устойчивость замкнутой системы, построив частотную характеристику разомкнутой системы:
(-)
L(s) – передаточная функция разомкнутой системы; L(jω) – частотная характеристика разомкнутой системы. Для каждой частоты ω значение L(jω) – это комплексное число, которое можно изобразить на комплексной плоскости. При изменении частоты от 0 до ∞, из этих точек складывается годограф Найквиста – кривая, начинающаяся при значении L(0) и заканчивающаяся в начале координат (так как L(s) – строго правильная функция, степень числителя меньше степени знаменателя). Система устойчива тогда и только тогда, когда годограф не охватывает точку (-1,0). 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 Х1
Х1 Х Х
Х Х


 Х2 Y = Х1 + Х2 - Х3
Х2 Y = Х1 + Х2 - Х3









 X Y1 Y X Y
X Y1 Y X Y




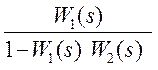












 W1(s)W2(s)] = W1(s) X(s)
W1(s)W2(s)] = W1(s) X(s)
 f
f






 X Y
X Y







 Y2
Y2





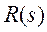










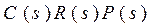



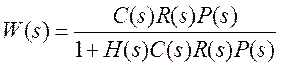














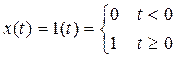
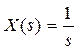













 . . .
. . . 





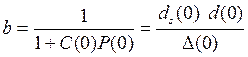


 при любых xi (i=0, 1, …, ν-1).
при любых xi (i=0, 1, …, ν-1).




 (-)
(-)

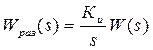
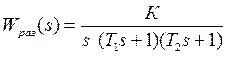 введем интегрирующее звено, получим:
введем интегрирующее звено, получим:
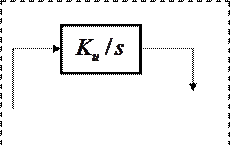





 (-)
(-)









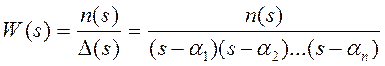

 при всех t, получаем:
при всех t, получаем: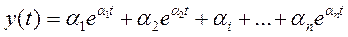



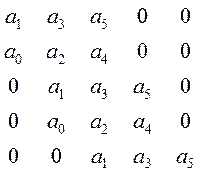
 > 0
> 0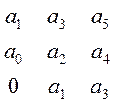 > 0
> 0