|
|
Типовые динамические звенья систем управленияВведение
Множество задач управления в современном мире связано с техническими системами (автомобили, самолеты, корабли, космические аппараты и станции, станки, производственное оборудование, горные машины и др.). Например, необходимо поддерживать: заданную высоту самолета, частоту вращения электродвигателя, курс корабля и т.д. Эти задачи решаются без участия человека. Принципы управления можно применять не только в технике, но и в других науках. Процессы управления и обработки информации в системах любой природы изучает наука – кибернетика. Один из ее разделов, связанных с техническими системами, называется теорией автоматического управления (теорией автоматического регулирования). Теория автоматического управления занимается классическими задачами регулирования, оптимизацией законов управления, вопросами адаптации и др.
Состав системы управления В задачах управления имеется два объекта: · управляемый объект (объект управления) – двигатель, корабль, самолет и т.д.; · управляющий объект (регулятор) – электрическая (электронная) схема или устройство, микропроцессорный контроллер, компьютер. Регулятор действует на объект управления не прямо, а через исполнительные механизмы, которые могут усиливать и (или) преобразовывать сигнал управления. Для того, чтобы оценить фактическое состояние объекта управления, регулятору необходимы сигналы с датчиков. В состав системы управления, как правило, входят следующие элементы: 1. Объект управления. 2. Регулятор. 3. Привод (исполнительный механизм) 4. Датчики. 5. Канал связи для обмена информацией между элементами системы (электрический ток, воздух, жидкость, компьютерные сети). Взаимосвязь указанных элементов является системой, которая обладает за счет связей особыми свойствами. Кроме того: · на объект управления действует окружающая среда в виде внешних возмущений. Они непредсказуемы и имеют случайный характер; · датчики измеряют параметры неточно, а с некоторой ошибкой (шум измерений). В системах управления есть обратная связь (ОС): регулятор использует информацию о состоянии объекта для выработки управления. Системы с ОС называются замкнутыми системами. Замкнутая система управления:
управление внешние задание возмущения
ОС
Система с управлением по ошибке (по отклонению):
ОС
Разомкнутая система управления (система программного управления):
управление внешние
Классификация систем управления Системы управления классифицируются по следующим признакам: 1. По степени участия человека: · автоматические (без участия человека); · автоматизированные (человек управляет и принимает решения). 2. По типу описываемых операторов: · линейные; · нелинейные. 3. По задачам управления: · системы стабилизации (поддержание заданного режима работы, не меняющегося длительное время); · системы программного управления (задание изменятся по известной программе); · системы слежения (воспроизведение на выходе неизвестного задающего сигнала). 4. По количеству входов и выходов: · одномерные (один вход, один выход); · многомерные (несколько входов и (или) несколько выходов). 5. По характеру сигналов: · непрерывные (аналоговые): описываются дифференциальными уравнениями – все сигналы – это функции непрерывные во времени, определенные на некотором временном интервале; · дискретные (импульсные, цифровые): описываются разностными уравнениями – все сигналы дискретные (последовательности чисел), определенные только в отдельные моменты времени; · непрерывно-дискретные: в них имеются как и аналоговые, так и дискретные сигналы. 6. По изменению характеристик объекта со временем: · стационарные: все параметры не изменяются во времени; · нестационарные: параметры изменяются с течением времени. 7. По изменению характеристик внешних воздействий и объекта управления: · детерминированные (все параметры определены точно); · стохастические (параметры изменяются случайным (вероятностным) образом). 8. Особые классы систем: · оптимальные (экстремальные: обеспечивают минимум или максимум критерия качества); · адаптивные (самонастраивающиеся: не могут быть нестационарными или стохастическими); · системы искусственного интеллекта; · системы управления, основанные на принципах нечеткой логики.
Математические модели Для исследования системы управления необходимо построить ее модель. Модель – объект, используемый для изучения другого объекта (оригинала). Любой объект взаимодействует с внешней средой при помощи входов и выходов. Входы – возможные воздействия на объект, выходы – сигналы, которые можно измерить. При изменении информации на входе меняется внутренне состояние объекта и, следовательно, меняется информация на выходах.
Оператор – правило преобразования вход Х в выход Y. Математические модели могут быть получены: · из законов физики (закон сохранения массы, закон сохранения энергии, закон сохранении импульса и др.); · в результате наблюдении за объектом при различных входных сигналах, при этом внутренне устройство объекта неизвестно. На практике используется смешанный способ: структура модели определяется из теории, а коэффициенты находят опытным путем. Кроме того, практикуется упрощение модели с целью несложной реализации закона управлении в реальной системе путем отбрасывания некоторых деталей.
Линейность и нелинейность Из математики известно, что проще всего решать линейные уравнения. Среди операторов линейные операторы саамы простые, они обладают следующими свойствами: · умножение на константу: U [a * X] = a * U [X], где: a - const; · принцип суперпозиции: U[X1 + X2] = U[X1] + U[X2] Используя линейные модели можно точно решать большинство практических задач управления, однако все модели реальных систем нелинейны. Методы исследования нелинейных операторов математически очень сложны: точные решения известны только для узкого круга задач. С целью решения этой проблемы, сначала проводят линеаризацию нелинейной модели объекта (построение приближенной линейной модели на основе реальной нелинейной), затем на основе этой модели проектируют закон управлении, применяя точные метод исследовании линейных систем, в итоге проверяют полученный регулятор (закон регулирования) на полной нелинейной модели при помощи компьютерного моделирования. Линеаризация заключается в подборе касательной к некоторой рабочей точке прямой с наклоном К и записи нелинейного уравнения модели в виде уравнений в отклонениях от точки, которой определялся наклон касательной. Реальные объекты не могут мгновенно изменять свое состояние, для их исследования используют динамические модели, описывающиеся дифференциальными уравнениями, которые включают в себя производные (скорости изменении сигналов). Дифференциальные уравнения точных моделей также нелинейны и для них требуется линеаризация. Принцип линеаризации в системах управления заключается в том, что сигналы в установившемся режиме мало отклоняются от рабочей точки и их производные равны нулю. Поэтому достаточно использовать линейную модель в отклонениях от этой рабочей точки (это справедливо только при малых отклонениях от рабочей точки).
Математические модели линейных объектов В качестве примера рассмотрим модель электродвигателя постоянного тока. Входом является напряжение якоря U(t); выходом является угол поворота вала двигателя θ(t) и угловая скорость вращения вала ω(t), при этом известно, что:
R
e U
Уравнение вращательного движения имеет вид:
где: J – суммарный момент инерции якоря и нагрузки; М(t) – вращающий момент; Mн(t) – момент нагрузки (возмущение).
ЭДС якоря определяется:
где: С ω – коэффициент; Ф – магнитный поток обмотки возбуждения.
Вращающий момент равен:
где: С м – коэффициент; i(t) – ток якоря.
Напряжение якоря определяется:
где: R – сопротивление якорной цепи.
Введем следующие коэффициенты: К 1 = С м Ф К 2 = С ω Ф
Получим и обозначим следующие уравнения:
Подставим уравнение (2) в выражение (4), учитывая уравнение 3, и выразим из него i(t), получим:
Полученное выражение подставим в уравнение (1) и перейдем к θ(t):
Полученное дифференциальное уравнение 2-го порядка является уравнением вход-выход и связывает вход U(t), выход θ(t) и нагрузку Mн(t). Необходимо отметить, что порядок модели соответствует порядку дифференциального уравнения. Модели в пространстве состояний Для того, чтобы упростить исследование модели объекта, желательно привести ее к некоторому стандартному виду, для которого уже есть готовые решения. Таким стандартом в теории управления считается система дифференциальных уравнений первого порядка, называемая нормальной формой Коши [1]. Вернемся к уже рассмотренному примеру – модели электродвигателя постоянного тока. Считаем: Mн(t) = 0, зная, что:
Запишем эту систему уравнений в матричной форме:
где: θ(t), ω(t) – переменные состояния;
В теории управления принято вектор состояния записывать X(t), вход объекта – через U(t), тогда модель «вход-состояние» (связывает вход U(t) и вектор состояния X(t)) имеет вид:
X’(t) = A * X(t) + B * U(t)
где:
Полная модель объекта в пространстве состояний содержит еще одно уравнение – уравнение выхода (оно показывает, как формируется выход объекта y(t)). Модель «вход-состояние-выход» имеет вид:
X’(t) = A * X(t) + B * U(t) y(t) = C * X(t) +D * U(t) В нашем примере: y(t) = θ(t) = [1 0]
Если y(t) = ω(t), то С = [0 1]. Изменяя матрицы C и D можно за выход принять любую линейную комбинацию переменных состояния. Так как величины J,R,K1 и K2 не зависят от времени, то матрицы A,B,C и D в модели постоянные и объект стационарен.
Переходная функция Один из методов построения моделей «вход-выход» является определение реакции объекта на некоторый стандартный сигнал. Один из простейших сигналов – единичный ступенчатый сигнал (скачок) 1(t):
Реакция объекта на единичной скачок называется переходной функцией. Объект должен иметь нулевые начальные условия (находиться в состоянии покоя). Если начальные условия ненулевые, то для построения сигнала выхода при любом входе нужно использовать дифференциальные уравнении объекта или модель в пространстве состояний. Переходная характеристика h(t) дает меньше информации, чем исходные уравнения. Ступенчатый сигнал нетрудно получить на практике и поэтому переходную характеристику можно получить экспериментально.
Импульсная характеристика (весовая функция) Импульсная функция – реакция системы на единичный импульс (дельта-функцию, функцию Дирака) δ(t):
Связь между импульсной и переходной функцией:
Импульсная характеристика – производная от переходной характеристики и, наоборот, переходная функция – интеграл от импульсной функции в интервале от 0 до t.
Передаточная функция Пусть модель объекта задана линейным дифференциальным уравнением второго порядка, связывающим вход x(t) и выход y(t):
где: ai, bi – постоянные. Введем оператор дифференцирования:
С учетом этого уравнение примет следующий вид:
Отсюда получим:
W(p) – передаточная функция объекта. Она полностью описывает связи между выходом и входом объекта при нулевых начальных условиях, но не учитывает его внутренние свойства. Правильная передаточная функция - степень ее числителя не больше степени знаменателя. Строго правильная передаточная функция – степень числителя меньше степени знаменателя. Неправильная передаточная функция – степень числителя больше степени знаменателя. Нули передаточной функции – корни числителя, полюса передаточной функции – корни знаменателя.
Преобразование Лапласа Для упрощения процедуры решения дифференциальных уравнений имеется преобразование, позволяющее заменить решение дифференциальных уравнений алгебраическими вычислениями (операциями с полиномами и рациональными функциями). Для функции f(t) вводится преобразование Лапласа:
где: F(s) – изображение функции-оригинала f(t), s – комплексная переменная. Обратное преобразование Лапласа имеет вид:
где: σ - постоянная; Часто на практике вместо этих интегралов используют готовые таблицы, по которым сразу определяют изображение по оригиналу и наоборот. Например:
Свойства преобразования Лапласа 1. Принцип суперпозиции :
2. Изображение для производной функции f(t) равно:
где: f(0) – значение f(t) при t=0. Аналогично, при нулевых начальных условиях i-ой производной изображение функции умножается на si.
4. При нулевых начальных условиях изображение выхода линейного объекта равняется произведению передаточной функции на изображение входного сигнала. Следовательно, передаточная функция определяется отношением изображения выходного сигнала к изображению входного сигнала при нулевых начальных условиях.
Передаточная функция и пространство состояний Модель «вход-состояние-выход» имеет вид:
X’(t) = A * X(t) + B * U(t) y(t) = C * X(t) +D * U(t) где: x(t) – вектор состояния.
Применим к этой модели преобразование Лапласа, получим: s * X(s) = A * X(s) + B * U(s) Y(s) = C * X(s) +D * U(s) X(s) (s*I – A) = B * U(s), где: I – единичная матрица (по главной диагонали в ней единицы, остальные элементы - нули).
X(s) = (s*I - A)-1 *B * U(s) Y(s) = C * (s*I - A)-1 *B * U(s) + D * U(s) = [C * (s*I - A)-1 *B + D]*U(s)
Передаточная функции равна:
Обратный переход (от передаточной функции к модели в пространстве состояний) более сложен, так как каждой передаточной функции соответствует множество моделей в пространстве состояний.
Частотные характеристики Гармонический сигнал (синус, косинус) является популярным эталонным сигналом при исследовании систем. Пусть на входе имеется гармонический сигнал вида: x(t) = sin ωt, где: ω – угловая частота, рад / с.
На выходе линейной системы в установившемся режиме будет синус той же частоты, но с другой амплитудой А и сдвигом фазы φ: y(t)= A(ω) sin [ωt+ φ(ω)]
Зная передаточную функцию системы W(s) и заменив комплексную переменную s на jω, при этом A(ω) = |W(j ω)| Для каждой частоты ω:
Функция W(j ω) является частотной характеристикой, она характеризует выход системы при гармонических сигналах разной частоты. A(ω) – амплитудно-частотная характеристика (АЧХ); φ(ω) – фазово-частотная характеристика (ФЧХ). Если на частоте ω: A(ω) > 1 – сигнал усиливается, A(ω) < 1 – сигнал ослабляется. Частотные характеристики можно получить экспериментально, если объект устойчивый.
Логарифмические частотные характеристики Применяются для проектирования регуляторов систем с помощью ручных вычислений и построений. Вместо A(ω) используется логарифмическая АЧХ (ЛАЧХ) L(ω):
Амплитуда L(ω) отображается на оси ординат, на оси абцисс отображается значение lgω. В логарифмической ФЧХ на оси ординат отображается фаза φ(ω), а на оси абцисс - lgω. Единица отсчета на логарифмической оси – декада, диапазон на котором частота увеличивается в 10 раз, а ее логарифм увеличивается на единицу. Для произведения передаточных функций W1(s) и W2(s) логарифмические характеристики представляют сумму характеристик каждого звена:
Типовые динамические звенья систем управления
Для исследования процессов в реальных системах пользуются идеализированными схемами, которые точно описываются математически и приближенно характеризуют реальные звенья систем в заданном диапазоне частот сигналов [1]. В общем случае передаточная функция системы может быть представлена в виде:
Звеном называют математическую модель элемента, соединения элементов или любой части системы. Обычно система управления состоит из отдельных блоков, каждый из которых, чаще всего, описывается обыкновенными линейными дифференциальными уравнениями не выше второго порядка. Рассматривая характеристики звеньев независимо от их назначения, физического принципа действия, мощности и скорости передаваемых сигналов, выделяют ряд типовых элементарных звеньев.
Усилительное (пропорциональное) звено Уравнение звена:
где: x(t) - выход звена; u(t) - входное воздействие; K - коэффициент усиления (статический коэффициент передачи) звена. С помощью усилительного звена передача сигнала от входа u(t) к выходу x(t)происходит мгновенно без какой-либо инерции. Поэтому усилительное звено называют еще пропорциональным, или безынерционным [1]. Передаточная функция усилительного звена:
Производя замену комплексной переменной s на jω, получим частотную характеристику усилительного звена:
Модуль выражения для W(jω) дает амплитудно-частотную характеристику (АЧХ) усилительного звена:
Поскольку мнимая часть в выражении для W(jω) равна нулю, то фазовая частотная характеристика (ФЧХ) будет равна нулю при всех частотах входного сигнала:
Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) усилительного звена равна:
Интегрирующие звенья
Идеальное интегрирующее звено Звено описывается дифференциальным уравнением первого порядка следующего вида:
где: k - коэффициент пропорциональности (усиления) звена. Коэффициент k численно равен скорости изменения выходной величины при единичном значении входной величины. Решая представленное выше дифференциальное уравнение получим:
Если начальные условия равны нулю, то, переходя к преобразованию Лапласа, получим передаточную функцию идеального интегрирующего звена:
Частотная характеристика интегрирующего звена равна:
АЧХ интегрирующего звена - это модуль частотной передаточной функции W(jω), т.е.:
ЛАЧХ интегрирующего звена:
При изменении частоты на одну декаду значение ЛАЧХ изменится на -20дБ. График ЛАЧХ представляет собой прямую линию с отрицательным наклоном. ФЧХ интегрирующего звена равна:
Интегрирующее звено с замедлением Звено описывается следующим дифференциальным уравнением [1]:
где: Т, k - постоянные параметры звена. Передаточная функция звена равна:
Частотная характеристика звена равна:
АЧХ звена определяется выражением:
ЛАЧХ звена строится по выражению:
ФЧХ звена равна:
Изодромное звено Дифференциальное уравнение изодромного звена имеет следующий вид [2]:
где: Т, k - постоянные параметры звена. Передаточная функция звена равна:
Частотная характеристика звена равна:
АЧХ звена равна:
ЛАЧХ изодромного звена равна:
ФЧХ звена определяется как:
Дифференцирующие звенья
Идеальное дифференцирующее звено Звено описывается следующим дифференциальным уравнением:
где: k - коэффициент пропорциональности (усиления) звена. Выходная величина x(t) дифференцирующего звена пропорциональна скорости изменения входной величины u(t). Передаточная функция идеального дифференцирующего звена:
Частотная характеристика звена равна:
Амплитудно-частотная характеристика звена:
ЛАЧХ дифференцирующего звена:
При изменении частоты на одну декаду значение ЛАЧХ изменится на +20дБ. График ЛАЧХ представляет собой прямую линию с положительным наклоном. ФЧХ получается из условия, что действительная часть частотной передаточной функции равна нулю:
Идеальное дифференцирующее звено относится к физически нереализуемым звеньям. В технике не могут использоваться физически не реализуемые звенья, поэтому для дифференцирования сигналов (ускорения реакции системы) используется инерционно-дифференцирующее звено (дифференцирующее звено с замедлением).
Дифференцирующее звено с замедлением (инерционно-дифференцирующее звено)
Фактически это звено представляет последовательное соединение двух звеньев: идеально дифференцирующего и апериодического звена первого порядка. Звено описывается дифференциальным уравнением вида:
где: Т, k - постоянные параметры звена. Передаточная функция звена равна:
Частотная характеристика звена равна:
АЧХ звена равна:
ЛАЧХ определяется как:
ФЧХ звена определяется как:
Апериодическое звено первого порядка Звено описывается дифференциальным уравнением первого порядка с постоянными коэффициентами:
где: Т, k - постоянная времени и статический коэффициент передачи звена. Постоянная времени звена характеризует его инерционные свойства, а статический коэффициент передачи (коэффициент усиления) представляет собой отношение выходного сигнала к входному в установившемся режиме (после завершения переходного процесса). Апериодическое звено первого порядка называют также инерционным звеном. Передаточная функция звена равна:
Производя замену комплексной переменной s на jω, получим частотную характеристику инерционного звена:
АЧХ звена равна:
Из выражения для АЧХ следует, что чем меньше постоянная времени Т, тем меньше инерционность звена и более вытянута амплитудная характеристика вдоль оси частот, или, как считается, тем шире полоса пропускания частот у данного звена [1]. ЛАЧХ апериодического звена первого порядка:
ФЧХ звена определяется как:
Апериодическое звено второго порядка Дифференциальное уравнение звена имеет следующий вид [1]:
где: Т1 ≥ 2Т2; Т1, Т2 - постоянные времени звена, k - коэффициент усиления звена. Передаточная функция звена равна:
где
Производя замену комплексной переменной s на jω, получим частотную характеристику апериодического звена второго порядка:
АЧХ звена равна:
ЛАЧХ апериодического звена второго порядка:
ФЧХ звена определяется как:
Колебательное звено Звено описывается дифференциальным уравнением второго порядка в двух формах:
где: Т1 < 2Т2, Т1, Т2 - постоянные времени звена, k - коэффициент усиления звена.
где: Т=Т2 - постоянная времени колебательного звена, 0 < ξ < 1 - относительный коэффициент затухания (коэффициент демпфирования), ξ = Т1 / 2Т2. Передаточная функция колебательного звена:
Производя замену комплексной переменной s на jω, получим частотную характеристику колебательного звена:
АЧХ звена равна:
ЛАЧХ колебательного звена:
Уравнение асимптотической ЛАЧХ имеет вид:
Частота ω = 1 / Т называется сопрягающей. Фазовую частотную характеристику колебательного звена представляют в следующем виде [4]:
Консервативное звено Консервативное звено является частным случаем колебательного звена при относительном коэффициенте затухания ξ=0. В консервативном звене не происходит рассеяния энергии. Уравнение консервативного звена:
Передаточная функция консервативного звена:
Частотная характеристика звена равна:
АЧХ звена равна:
ЛАЧХ консервативного звена:
Фазовая частотная характеристика консервативного звена определяется:
Запаздывающее звено Выходная величина в запаздывающем звене точно повторяет входную величину, но с некоторым запаздыванием по времени τ:
Найдем передаточную функцию запаздывающего звена, применив к приведенному уравнению прямое преобразование Лапласа, получим:
Введем новую переменную: z = t - τ:
Поскольку преобразование Лапласа определяется в пределах от нуля до бесконечности, то полученное выражение следует интегрировать в пределах от нуля до бесконечности, т.е.:
В полученном выражении интеграл - это преобразование Лапласа от входной величины, поэтому:
Теперь найдем передаточную функцию, взяв отношение изображения по Лапласу выходной величины к изображению входной:
Частотная характеристика запаздывающего звена с учетом формулы Эйлера равна:
Амплитудно-частотная характеристика:
ЛАЧХ запаздывающего звена:
ФЧХ звена равна:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 ошибка измерения
ошибка измерения






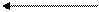








 ω i
ω i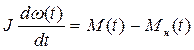



 (1)
(1) (2)
(2)




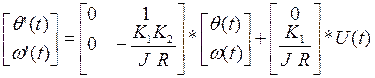
 - вектор состояния.
- вектор состояния.




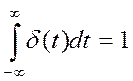



 , который действует на сигнал:
, который действует на сигнал: 





 .
.
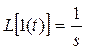





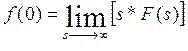







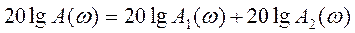




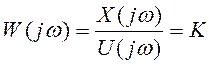
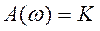
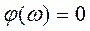
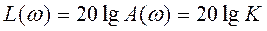




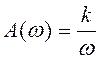

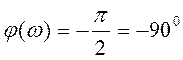
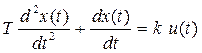


















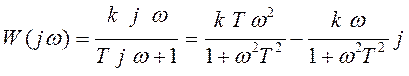


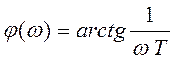
 Фазовые сдвиги, вносимые звеном, являются наибольшими при низких частотах. На высоких частотах фазовый сдвиг постепенно уменьшается, стремясь в пределе к нулю при ω ∞.
Фазовые сдвиги, вносимые звеном, являются наибольшими при низких частотах. На высоких частотах фазовый сдвиг постепенно уменьшается, стремясь в пределе к нулю при ω ∞.



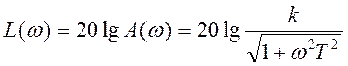


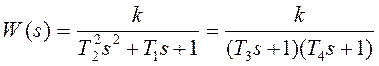
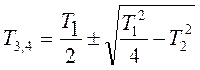


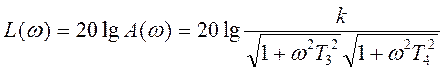







 при ω < 1 / T
при ω < 1 / T при ω ≥ 1 / T
при ω ≥ 1 / T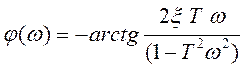 при ω ≤ 1 / T
при ω ≤ 1 / T при ω > 1 / T
при ω > 1 / T




 при ω > 1 / T
при ω > 1 / T .
.