
|
|
Электрическое поле в диэлектрикеЛекция 5 Граничные условия на поверхности раздела Диэлектрик-диэлектрик
1.1. Условие для вектора
Пусть на границе раздела двух диэлектриков находится сторонний поверхностный заряд. Для нахождения условия будем использовать теорему о циркуляции вектора
Электрическое поле вблизи границы раздела в диэлектрике 1 обозначим через
На основании теоремы о циркуляции вектора (Е1t*+ Е2t) где Е1t* и Е2t - проекции вектора Е1t = Е2t. (1) Вывод: Тангенциальная составляющая вектора 1.2. Условие для вектора Для нахождения условия для вектора Используя теорему Гаусса для вектора (D1n* + D2n) DS = s DS, где s - поверхностная плотность стороннего заряда на границе раздела.
С учетом того, что D1n* = - D1n последнее равенство принимает вид: D2n - D1n = s. (2) Вывод: нормальная составляющая вектора Если сторонние заряды отсутствуют на границе раздела, то D2n = D1n, (3) т. е. нормальная составляющая вектора Следовательно, если на границе раздела двух диэлектриков нет сторонних зарядов, то при переходе через границу составляющие Еt и Dn изменяются непрерывно, не испытывая скачка, а составляющие Еn и Dt - испытывают скачок. 1.3. Преломление линий
При переходе через границу линии напряженности и линии электрического смещения преломляются (рис. 3). Если на границе раздела нет сторонних зарядов, то из (1), (2) и (3) следует Е1t = Е2t, e1Е1n = e2Е2n. Согласно рис. 3 имеем
или
Следовательно, в диэлектрике с большим значением диэлектрической проницаемости (e2 > e1) линии напряженности и электрического смещения составляют больший угол с нормалью к границе раздела (рис. 4). На рис. 4 приведено графическое изображение поля Из рис. 4 следует, что Е2 < Е1 и D2 > D1. Кроме того, линии напряженности испытывают преломление и терпят разрыв из-за наличия связанных зарядов. Линии электрического смещения испытывают только преломление, так как на границе раздела нет сторонних зарядов.
Граничные условия на поверхности раздела Проводник-диэлектрик
На границе раздела: проводник-диэлектрик (среда 1 - проводник, среда 2 - диэлектрик) согласно формуле (2) имеем Dn = s, (6) где n - внешняя нормаль к поверхности проводника. Вывод: В состоянии равновесия электрическое поле внутри проводника отсутствует, следовательно, и его поляризованность равна нулю. Поэтому электрическое смещение равно нулю (D = 0) внутри проводника. Замечание: Если к поверхности заряженного проводника прилегает однородный изотропный диэлектрик, то на их границе появляются связанные заряды плотности s* (объемная плотность связанных зарядов r* = 0). Но на границе проводник-диэлектрик есть сторонние и связанные заряды. Поэтому, применяя теорему Гаусса к вектору
или
Из сравнения последних двух равенств следует, что
В итоге получим, что
Вывод: Поверхностная плотность сторонних зарядов s на проводнике однозначно связана с поверхностной плотностью связанного заряда s* в диэлектрике, но знаки этих зарядов противоположны. Электрическое поле в диэлектрике
При внесении изотропного диэлектрика во внешнее электрическое поле Внутри диэлектрика связанные заряды компенсируют друг друга. На левой грани возникает не скомпенсированный связанный отрицательный заряд с поверхностной плотностью - s*,, а на правой - положительный связанный заряд с поверхностной плотностью + s*. В диэлектрике возникнет свое электрическое поле Е*= направлено противоположно внешнему полю Согласно принципу суперпозиции результирующее электрическое поле
или по абсолютной величине Е = Е0 - Е* . (10)
В отсутствии диэлектрика электрическое поле плоского конденсатора в вакууме характеризуется электрическим смещением и напряженностью
Поскольку внутри диэлектрика напряженность электрического поля
Е = Е0 - Е*, то с учетом (8), (10) и (12) получим, что
Это поле перпендикулярно боковым граням изотропного диэлектрика, поэтому Еn = E. Так как s* = æe0Е, (14) то формулу (13) перепишем в виде Е = Е0 - æЕ или
Электрическое смещение внутри диэлектрика:
D = e0eE = e0E = D0. (16)
Следовательно, электрическое смещение внутри диэлектрика совпадает с электрическим смещением внешнего электрического поля в вакууме D0. Используя формулу (13) на основании (16) получаем, что D = s. (17) Вывод: Электрическое смещение численно равно поверхностной плотности сторонних зарядов.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 , и теорему Гаусса для вектора
, и теорему Гаусса для вектора  , т. е.
, т. е. .
. Рис. 1
Рис. 1
 = 0,
= 0, , взяты в направлении обхода контура (на рис. 1 указан стрелками). Если использовать в качестве общего единичный вектор
, взяты в направлении обхода контура (на рис. 1 указан стрелками). Если использовать в качестве общего единичный вектор  , то Е1t* = - Е1t. Тогда предыдущее равенство принимает вид
, то Е1t* = - Е1t. Тогда предыдущее равенство принимает вид одинакова по разные стороны границы раздела, т. е. не испытывает скачка.
одинакова по разные стороны границы раздела, т. е. не испытывает скачка.
 Рис. 2
Рис. 2

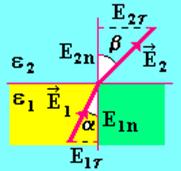 Рис. 3
Рис. 3

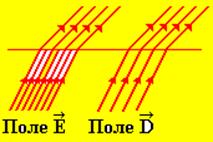 Рис. 4
Рис. 4
 . (4)
. (4) и
и  на границе раздела двух изотропных, однородных диэлектриков, у которых нет сторонних зарядов и e2 > e1.
на границе раздела двух изотропных, однородных диэлектриков, у которых нет сторонних зарядов и e2 > e1.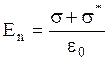 .
. .
.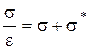 .
. . (7)
. (7) Рис. 5
Рис. 5
 , (8)
, (8) . (12)
. (12) . (13)
. (13) . (15)
. (15)