|
|
Свойства логарифмической функции.12 1. Область определения логарифмической функции – промежуток (0; +¥). 2. Область значения логарифмической функции – вся числовая прчмая. 3. Логарифмическая функция непрерывна и дифференцируема во всей области определения. Производная логарифмической функции вычисляется по формуле
(loga x)¢ = 1/(x ln a).
4. Логарифмическая функция монотонно возрастает, если а>1. При 0<a<1 логарифмическая функция с основанием а монотонно убывает. 5. При любом основании a>0, a¹1, имеют место равенства
loga 1 = 0, loga a =1. 6. При а>1 график логарифмической функции – кривая, направленная вогнутостью вниз; при 0<a<1 – кривая, направленная вогнутостью вверх.
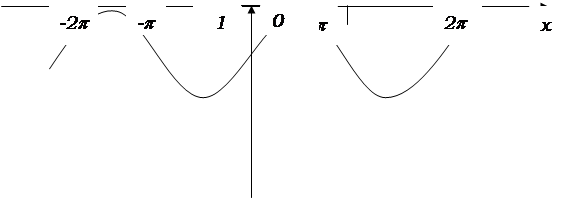
График логарифмической функции при а=2 изображен на рис. 6.
Рис. 6 Основное логарифмическое тождество. Обратной функцией для показательной функции y=axбудет логарифмическая функция x =loga y. По свойствам взаимно обратных функций f и f-I f(f-I (y))=y для всех x из области определения функции f-I(х). В частности, для показательной и логарифмической функции равенство (1) принимает вид alogay=y. Равенство (2) часто называют основным логарифмическим тождеством. При любых положительных х, у для логарифмической функции верны следующие равенства, которые могут быть получены как следствия основного логарифмического тождества (2) и свойства показательной функции: loga (x×y)=loga x+loga y; loga (x/y)= loga x-loga y; loga (xa)=a× loga x (a - любое действительное число); logaa=1; loga x =( logb x/ logb a) (b – действительное число, b>0, b¹1). В частности из последней формулы при а=е, b=10 получается равенство
ln x = (1/(ln e))lg x. (3)
Число lg e называют модулем перехода от натуральных логарифмов к десятичным и обозначают буквой М, а формулу (3) обычно записывают в виде
lg x =M× ln x.
Обратно пропорциональная зависимость Переменную y называют обратно пропорциональной переменной x, если значения этих переменных связаны равенством y = k/x, где k – некоторое действительное число, отличное от нуля. Число k называют коэффициентом обратной пропорциональности. Если считать x независимой переменной, а y – зависимой, то формула y = k/x определяет y как функцию от x. График функции y = k/x называется гиперболой.
Рис. 7
Свойства функции y = k/x. 1. Область определения функции – множество всех действительных чисел, за исключением числа 0. 2. Область значения функции – множество всех действительных чисел, за исключением числа 0. 3. Функция f(x) = k/x – нечетная, и ее график симметричен относительно начала координат. Функция f(x) = k/x непрерывна и дифференцируема во всей области определения. f(x)¢ = -k/x2. Функция критических точек не имеет. 4. Функция f(x) = k/x при k>0 монотонно убывает в (-¥, 0) и (0, +¥), а при k<0 монотонно возрастает в тех же промежутках. 5. График функции f(x) = k/x при k>0 в промежутке (0, +¥) направлен вогнутостью вверх, а в промежутке (-¥, 0) – вогнутостью вниз. При k<0 промежуток вогнутости вверх (-¥, 0), промежуток вогнутости вниз (0, +¥). График функции f(x) = k/x для значения k=1 изображен на рис. 7.
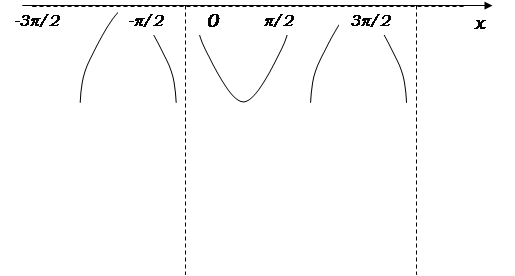
Тригонометрические функции Функции sin a, cos a, tg a, ctg a называются тригонометрическими функциями угла a. Кроме основных тригонометрических функций sin a, cos a, tg a, ctg a существуют еще две тригонометрические функции угла a - секанс и косеканс, обозначаемые sec a и cosec a соответственно. Sin х Синусом числа х называется число, равное синусу угла в радианах. Свойства функции sin х. 1. Область определения – множество всех действительных чисел. 2. Область значения – промежуток [-1; 1]. 3. Функцияsin х – нечетная: sin (-х)=- sin х. 4. Функция sin х – периодическая. Наименьший положительный период равен 2p: sin (х+2p)= sin х. 5. Нули функции: sin х=0 при x=pn, n Î Z. 6. Промежутки знакопостоянства: sin х>0 при x Î (2pn; p+2pn), n Î Z, sin х<0 при x Î (p+2pn; 2p+2pn), n Î Z. 7. Функция sin х непрерывна и имеет производную при любом значении аргумента: (sin х)¢ =cos x. 8. Функция sin х возрастает при xÎ ((-p/2)+2pn; (p/2)+2pn), n Î Z, и убывает при xÎ ((p/2)+2pn; ((3p)/2)+ 2pn), n Î Z. 9. Функция sin х имеет минимальные значения, равные –1, при х=(-p/2)+2pn, n Î Z, и максимальные значения, равные 1, при х=(p/2)+2pn, n Î Z. График функции y=sin х изображен на рис. 8. График функции sin х называют синусоидой.
Рис. 8 Свойства функции cos х. 1. Область определения – множество всех действительных чисел. 2. Область значения – промежуток [-1; 1]. 3. Функцияcos х – четная: cos (-х)=cos х. 4. Функция cos х – периодическая. Наименьший положительный период равен 2p: cos (х+2p)= cos х. 5. Нули функции: cos х=0 при x=(p/2)+2pn, n Î Z. 6. Промежутки знакопостоянства: cos х>0 при x Î ((-p/2)+2pn; (p/2)+2pn)), n Î Z, cos х<0 при x Î ((p/2)+2pn); ((3p)/2)+ 2pn)), n Î Z. 7. Функция cos х непрерывна и дифференцируема при любом значении аргумента: (cos х)¢ =-sin x. 8. Функция cos х возрастает при xÎ (-p+2pn; 2pn), n Î Z, и убывает при xÎ (2pn; p+ 2pn), n Î Z. 9. Функция cos х имеет минимальные значения, равные –1, при х=p+2pn, n Î Z, и максимальные значения, равные 1, при х=2pn, n Î Z.
Рис. 9
Свойства функции tg х. 1. Область определения функции – множество всех действительных чисел, кроме числа х=p/2+pn, n Î Z. 2. Область значения – множество всех действительных чисел. 3. Функцияtg х – нечетная: tg (-х)=- tg х. 4. Функция tg х – периодическая. Наименьший положительный период функции равен p: tg (х+p)= tg х. 5. Нули функции: tg х=0 при x=pn, n Î Z. 6. Промежутки знакопостоянства: tg х>0 при x Î (pn; (p/2)+pn), n Î Z, tg х<0 при x Î ((-p/2)+pn; pn), n Î Z. 7. Функция tg х непрерывна и дифференцируема при любом значении аргумента из области определения: (tg х)¢ =1/cos2 x. 8. Функция tg х возрастает в каждом из промежутков ((-p/2)+pn; (p/2)+pn), n Î Z, График функции y=tg х изображен на рис. 10. График функции tg х называют тангенсоидой.
Свойства функции сtg х. 1. Область определения функции – множество всех действительных чисел, кроме чисел вида х=pn, n Î Z. 2. Область значения – множество всех действительных чисел. 3. Функциясtg х – нечетная: сtg (-х)=- сtg х. 4. Функция сtg х – периодическая. Наименьший положительный период функции равен p: сtg (х+p)= ctg х. 5. Нули функции: ctg х=0 при x=(p/2)+pn, n Î Z. 6. Промежутки знакопостоянства: ctg х>0 при x Î (pn; (p/2)+pn), n Î Z, ctg х<0 при x Î ((p/2)+pn; p(n+1)), n Î Z. 7. Функция ctg х непрерывна и дифференцируема при любом значении аргумента из области определения: (ctg х)¢ =-(1/sin2 x). 8. Функция ctg х убывает в каждом из промежутков (pn; p(n+1)), n Î Z. График функции y=сtg х изображен на рис. 11.
Рис.11
Свойства функции sec х. 1. Область определения функции – множество всех действительных чисел, кроме чисел вида х=(p/2)+pn, n Î Z. 2. Область значения: (-¥; 1]È[1; +¥). 3. Функцияsec х – четная: sec (-х)= sec х. 4. Функция sec х – периодическая. Наименьший положительный период функции равен 2p: sec (х+2p)= sec х. 5. Функция sec x ни при каком значении аргумента не обращается в нуль. 6. Промежутки знакопостоянства: sec х>0 при x Î ((-p/2)+2pn; (p/2)+2pn), n Î Z, sec х<0 при x Î ((p/2)+2pn; (3p/2)+2pn), n Î Z. 7. Функция sec х непрерывна и дифференцируема при любом значении аргумента из области определения функции: (sec х)¢ =sin x/cos2 x. 8. Функция sec х возрастает в промежутках (2pn; (p/2)+ 2pn), ((p/2)+ 2pn; p+ 2pn], n Î Z, и убывает в промежутках [p+ 2pn; (3p/2)+ 2pn), ((3p/2)+ 2pn; 2p(n+1)], n Î Z.
График функции y=sec х изображен на рис. 12.
Рис. 12

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|