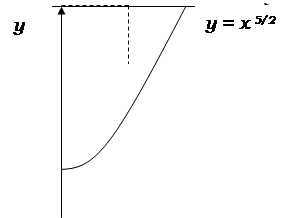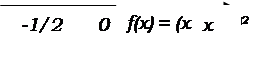Свойства показательной функции.

Реферат по математике

«элементарные функции»

Выполнила:

студентка 1 курса

факультета информатики

11 группы

Дивейко н.в.

проверил:

адольф в. а.

г. Красноярск 2001 г.

план

I. введение

II. свойства и графики элементарных функций

Степенная функция

Квадратичная функция

Показательная функция

Логарифмическая функция

Обратно пропорциональная зависимость

Тригонометрические функции

III. мои примеры графиков

IV. Список использованной литературы

I. введение

К элементарным функциям относятся рациональные, степенные, показательная и логарифмические функции, а также тригонометрические и обратные тригонометрические функции. К классу элементарных функций, кроме того относят также сложные функции, образованные из перечисленных выше элементарных функций.

II. свойства и графики элементарных функций

Степенная функция

Степенной функцией называется функция вида f(x)=x^a, где a - любое действительное число, называемое показателем степени.

Свойства степенной функции.

1. Область определения степенной функции – множество всех положительных чисел.

2. Область значения степенной функции – множество всех положительных чисел.

3. Степенная функция непериодична, не является четной и не является нечетной.

4. Степенная функция непрерывна во всей области определения.

5. Степенная функция дифференцируема во всей области определения, и ее производная вычисляется по формуле

(x^a)¢= a^.x^a-1.

6. Степенная функция x^a монотонно возрастает во всей области определения при a<0.

Рис. 1 Рис. 2

7. При a<0 и a>1 график степенной функции направлен вогнутостью вверх, а при 0<a<1 – вогнутостью вниз.

Графики степенной функции при некоторых значениях a приведены на Рис. 1 и Рис. 2.

Квадратичная функция

Функция f(x)=ax²+bx²+c, где a, b, c – некоторые действительные числа (a¹0), называется квадратичной функцией. График квадратичной функции называется параболой.

Квадратичная функция может быть приведена к виду

f(x)=a(x+b/2a)²-(b²-4ac)/4a, (1)

выражение b²-4ac называется дискриминантом квадратного трехчлена. Представление квадратной функции в виде (1) называется выделением полного квадрата.

Свойства квадратичной функции и ее график

1. Область определения квадратичной функции – вся числовая прямая.

2. При b¹0 функция не является четной и не является нечетной. При b=0 квадратичная функция – четная.

Рис. 3 Рис. 4

3. Квадратичная функция непрерывна и дифференцируема во всей области определения.

4. Функция имеет единственную критическую точку

x=-b/(2a). Если a>0, то в точке x=-b/(2a) функция имеет минимум. При x<-b/(2a) функция монотонно убывает, при x>-b/(2a) монотонно возрастает.

Если а<0, то в точке x=-b/(2a) функция имеет максимум. При x<-b/(2a) функция монотонно возрастает, при x>-b/(2a) монотонно убывает.

Точка графика квадратичной функции с абсциссой x=-b/(2a) и ординатой y= -((b²-4ac)/4a) называется вершиной параболы.

5. Область изменения функции: при a>0 – множество значений функции [-((b²-4ac)/4a); +¥); при a<0 – множество значений функции (-¥;-((b²-4ac)/4a)].

6. График квадратичной функции пересекается с осью 0y в точке y=c. В случае, если b²-4ac>0, график квадратичной функции пересекает ось 0x в двух точках (различные действительные корни квадратного уравнения); если b²-4ac=0 (квадратное уравнение имеет один корень кратности 2), график квадратичной функции касается оси 0x в точке x=-b/(2a); если b²-4ac<0, пересечения с осью 0x нет.

Из представления квадратичной функции в виде (1) также следует, что график функции симметричен относительно прямой x=-b/(2a) – образа оси ординат при параллельном переносе r=(-b/(2a); 0).

График функции

f(x)=ax²+bx+c

(или f(x)=a(x+b/(2a))²-(b²-4ac)/(4a)) может быть получен из графика функции f(x)=x² следующими преобразованиями:

а) параллельным переносом r=(-b/(2a); 0);

б) сжатием (или растяжением) к оси абсцисс в а раз;

в) параллельным переносом r=(0; -((b²-4ac)/(4a))).

Показательная функция

Показательной функцией называется функция вида f(x)=a^x, где а – некоторое положительное действительное число, называемое основанием степени. При а=1 значение показательной функции при любом значении аргумента равно единице, и случай а=1 далее не будет рассматриваться.

Свойства показательной функции.

1. Область определения функции – вся числовая прямая.

2. Область значения функции – множество всех положительных чисел.

3. Функция непрерывна и дифференцируема во всей области определения. Производная показательной функции вычисляется по формуле

(a^x)¢ =a^xlna

4. При а>1 функция монотонно возрастает, при а<1 монотонно убывает.

5. Показательная функция имеет обратную функцию, называемую логарифмической функцией.

6. График любой показательной функции пересекает ось 0y в точке y=1.

7. График показательной функции – кривая, направленная вогнутостью вверх.

Рис. 5

Логарифмическая функция

Функцию, обратную показательной функции y=a^x, называют логарифмической и обозначают

y=log_a x.

Число а называется основанием логарифмической функции. Логарифмическую функцию с основанием 10 обозначают

lg x,

а логарифмическую функцию с основанием е обозначают

ln x.

Не нашли, что искали? Воспользуйтесь поиском по сайту: