
|
|
Неопределенные интегралы.12 1.Найти все первообразные функции 2.Вычислить интеграл 3.Вычислить интеграл 4.Вычислить интеграл 5.Вычислить интеграл 6.Для интеграла 7.Для подынтегральной функции Определенные интегралы. 1.Вычислить интеграл 2.Функция
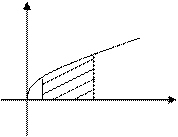
4.Вычислить площадь фигуры, изображенной на рисунке 1 5 5.Вычислить площадь фигуры, ограниченной линиями 6.Вычислить объем тела вращения, полученного вращением фигуры Контрольная работа № 2 для студентов ИДПО (направление ЭС) Вариант 7. Комплексные числа 1. 2. 3. 4. 5. Неопределенные интегралы. 1.Найти все первообразные функции 2.Вычислить интеграл 3.Вычислить интеграл 4.Вычислить интеграл 5.Вычислить интеграл 6.Для интеграла 7.Для подынтегральной функции Определенные интегралы. 1.Вычислить интеграл 2.Даны интегралы
4.Вычислить площадь фигуры, изображенной на рисунке 1 4 5.Вычислить площадь фигуры, ограниченной линиями 6.Вычислить объем тела вращения, полученного вращением фигуры Контрольная работа № 2 для студентов ИДПО (направление ЭС) Вариант 8. Комплексные числа 1. 2. 3. 4. 5. Неопределенные интегралы. 1.Найти все первообразные функции 2.Вычислить интеграл 3.Вычислить интеграл 4.Вычислить интеграл 5. Вычислить интеграл 6.Для подынтегральной функции 7.Для подынтегральной функции Определенные интегралы. 1.Вычислить интеграл 2Даны интегралы
4.Вычислить площадь фигуры, изображенной на рисунке 5.Вычислить площадь фигуры, ограниченной линиями 6.Вычислить объем тела вращения, полученного вращением фигуры Контрольная работа № 2 для студентов ИДПО (направление ЭС) Вариант 9. Комплексные числа 1. 2. 3. 4. 5. Неопределенные интегралы. 1.Найти все первообразные функции 2.Вычислить интеграл 3.Вычислить интеграл 4.Вычислить интеграл 5.Вычислить интеграл 6.Найтиразложение и значения коэффициентов для подынтегральной функции 7.Для подынтегральной функции Определенные интегралы. 1.Вычислить интеграл 2.Даны интегралы
4.Вычислить площадь фигуры, изображенной на рисунке 1 4 5.Вычислить площадь фигуры, ограниченной линиями 6.Вычислить объем тела вращения, полученного вращением фигуры Контрольная работа № 2 для студентов ИДПО (направление ЭС) Вариант 10.
Комплексные числа 1. 2. 3. 4. 5. Неопределенные интегралы. 1.Найти все первообразные функции 2.Вычислить интеграл 3.Вычислить интеграл 4.Вычислить интеграл 5.Вычислить интеграл 6.Найтиразложение и значения коэффициентов для подынтегральной функции 7.Для подынтегральной функции Определенные интегралы. 1.Вычислить интеграл 2.Функция
4.Вычислить площадь фигуры, изображенной на рисунке 2 5 5.Вычислить площадь фигуры, ограниченной линиями 6.Вычислить объем тела вращения, полученного вращением фигуры Контрольная работа № 2 для студентов ИДПО (направление ЭС) Вариант 11. Комплексные числа 1. 2. 3. 4. 5. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. .
. .
.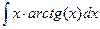 .
. .
. записать вид разложения на дроби и найти коэффициенты.
записать вид разложения на дроби и найти коэффициенты. записать вид разложения на дроби.
записать вид разложения на дроби. .
. является четной, и
является четной, и  . Найти
. Найти  .
. 3.Даны интегралы
3.Даны интегралы  и
и  . Найти значение интеграла
. Найти значение интеграла 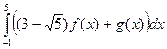 .
.
 .
. вокруг оси
вокруг оси  .
. . Найти
. Найти  .
. . Найти
. Найти  .
. . Записать в тригонометрической форме число
. Записать в тригонометрической форме число 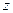 .
.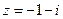 . Найти
. Найти  .
.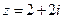 . Найти
. Найти  .
. .
. .
.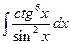 .
. .
.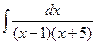 .
. записать вид разложения на дроби и найти значения коэффициентов.
записать вид разложения на дроби и найти значения коэффициентов. записать вид разложения на дроби.
записать вид разложения на дроби. .
. и
и  . Найти
. Найти  .
. 3.Даны интегралы
3.Даны интегралы 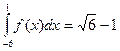 и
и  . Найти значение интеграла
. Найти значение интеграла  .
.
 .
. вокруг оси
вокруг оси  . Найти
. Найти  .
. . Записать в тригонометрической форме число
. Записать в тригонометрической форме число 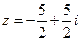 . Найти
. Найти 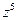 .
.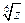 .
. .
. .
. .
.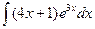 .
. .
.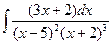 записать вид разложения на простейшие дроби и найти значения коэффициентов.
записать вид разложения на простейшие дроби и найти значения коэффициентов. записать вид разложения на простейшие дроби.
записать вид разложения на простейшие дроби.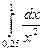 .
. и
и  . Найти
. Найти  3.Даны интегралы
3.Даны интегралы  и
и  . Найти значение интеграла
. Найти значение интеграла  .
.
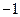

 .
.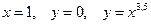 вокруг оси
вокруг оси  . Найти
. Найти  .
. . Найти
. Найти  . Найти
. Найти  . Найти
. Найти  .
. .
. .
. .
. .
. .
. записать вид разложения на простейшие дроби.
записать вид разложения на простейшие дроби.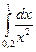 .
. . Найти
. Найти  3.Даны интегралы
3.Даны интегралы  и
и 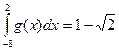 . Найти значение интеграла
. Найти значение интеграла  .
.
 .
.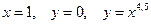 вокруг оси
вокруг оси  . Найти
. Найти  . Записать в тригонометрической форме число
. Записать в тригонометрической форме число 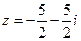 . Найти
. Найти 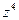 .
. . Найти
. Найти  .
. .
. .
. .
. .
. .
. записать вид разложения на простейшие дроби.
записать вид разложения на простейшие дроби.  .
. . Найти
. Найти  .
. 3.Даны интегралы
3.Даны интегралы 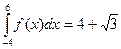 и
и  . Найти значение интеграла
. Найти значение интеграла  .
.
 .
. вокруг оси
вокруг оси  .
. .
.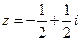 . Найти
. Найти  . Найти
. Найти