
|
|
Математическое описание функциональных элементов
Математическое описание каждого функционального элемента следует проводить в отдельном подразделе с указанием заголовка, например: 1.1 Электронный усилитель 1.2 Генератор постоянного тока и т.д. Для каждого функционального элемента привести его принципиальную схему, дать краткое описание принципа действия (например, пояснить каким образом достигается усиление сигнала по мощности в генераторе и ЭМУ). С описанием функциональных элементов можно ознакомиться в [1-5]. При выводе уравнений функциональных элементов с учетом принятых допущений нет необходимости проводить линеаризацию уравнений и записывать уравнения в малых отклонениях от номинального режима. Здесь уравнения функциональных элементов линейные и изменение их координат могут быть большими. При записи уравнений и передаточных функций рекомендуется использовать следующий способ обозначений: например, Допускается сквозная нумерация формул или нумерация формул в пределах одного раздела (например, (2.4) и т.п.). Определение параметров электрических машин проводится по паспортным данным таблицы 1, которые соответствуют номинальным режимам при источнике питания бесконечной мощности (с нулевым внутренним сопротивлением). При этом коэффициенты передачи определяются из уравнений статики. С помощью найденных паспортных значений коэффициентов передачи определяются коэффициенты передачи и постоянные времени передаточных функций для соединенных блоков функциональных элементов ("электронный усилитель-ЭМУ" в схемах А, Б, В; "электронный усилитель-генератор" в схемах Г, Д; "генератор-двигатель" в схемах А, Б, Г, Д) с учетом внутренних сопротивлений источников напряжения. Ниже приводятся примеры определения параметров передаточных функций для функциональных элементов. Расчеты проводятся в системе единиц СИ.
Генератор постоянного тока
1. Уравнения статики для номинального режима генератора имеют вид
где Отсюда следует, что
и с учетом паспортных значений найдем коэффициент усиления генератора
Например, для генератора №1 получим
2. Уравнения динамики генератора в схеме соединения имеют вид
где Отсюда с учетом преобразования Лапласа при нулевых начальных условиях получим
где Например, коэффициент усиления генератора для схем Г, Д имеет значение
т.е. меньше паспортного значения. 3. Для генератора с нагрузкой
где
В установившемся номинальном режиме при отсутствии нагрузки
Учитывая малость величины
Фрагмент структурной схемы генератора с нагрузкой представлен на рис. 10.
Тахогенератор
1. Тахогенератор постоянного тока предназначен для измерения угловой скорости вращения якоря. Уравнения статики для номинального режима следуют из уравнений статики генератора без учета малого сопротивления
где Отсюда следует, что
где
Например, для тахогенератора №1 получим
2. Уравнения динамики тахогенератора имеют вид
Тогда передаточная функция тахогенератора для схем А,Б имеет вид
Для схем Г, Д выходом тахогенератора является угловое перемещение

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 – коэффициент усиления электронного усилителя,
– коэффициент усиления электронного усилителя,  – передаточная функция электронного усилителя;
– передаточная функция электронного усилителя;  , где
, где  – передаточная функция, связывающая выход
– передаточная функция, связывающая выход  с входом
с входом 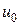 и т.п. (другие обозначения см. ниже).
и т.п. (другие обозначения см. ниже). ,
, ,
, ,
, и
и  – номинальные напряжение и ток в обмотке возбуждения генератора,
– номинальные напряжение и ток в обмотке возбуждения генератора,  – номинальное значение э.д.с.;
– номинальное значение э.д.с.;  и
и  – номинальные напряжение и ток в якорной обмотке генератора,
– номинальные напряжение и ток в якорной обмотке генератора,  – сопротивление управляющей обмотки возбуждения генератора;
– сопротивление управляющей обмотки возбуждения генератора;  – сопротивление якорной обмотки генератора;
– сопротивление якорной обмотки генератора; 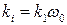 – коэффициент усиления по току, зависящий от угловой скорости вращения
– коэффициент усиления по току, зависящий от угловой скорости вращения  якоря вспомогательного двигателя. В генераторах, предназначенных для усиления напряжения по мощности,
якоря вспомогательного двигателя. В генераторах, предназначенных для усиления напряжения по мощности,  .
. ,
, .
. .
. ,
, ,
, ,
,  ,
,  – сопротивление якоря ЭМУ – для схем А, Б, В;
– сопротивление якоря ЭМУ – для схем А, Б, В;  ,
,  ,
,  – выходное сопротивление электронного усилителя – для схем Г, Д.
– выходное сопротивление электронного усилителя – для схем Г, Д. с передаточной функцией
с передаточной функцией ,
, ,
,  .
. ,
, в схеме В напряжение на нагрузке определяется по формуле
в схеме В напряжение на нагрузке определяется по формуле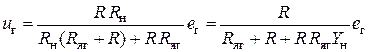 ,
, ;
; 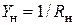 – проводимость нагрузки. Отсюда следует, что напряжение
– проводимость нагрузки. Отсюда следует, что напряжение  является нелинейной функцией от величин
является нелинейной функцией от величин  ,
,  . Учитывая, что при наличии нагрузки
. Учитывая, что при наличии нагрузки 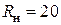 Ом величина
Ом величина  , с помощью разложения в ряд Тейлора можно записать
, с помощью разложения в ряд Тейлора можно записать .
. (
( 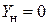 ) справедливо уравнение
) справедливо уравнение .
. , отклонения
, отклонения  ,
,  вызванные подключением нагрузки
вызванные подключением нагрузки  будет справедливо уравнение
будет справедливо уравнение .
.
 ,
, – номинальные обороты якоря;
– номинальные обороты якоря;  .
.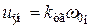 ,
, .
. Вс/рад.
Вс/рад. .
. .
. . В этом случае с учетом равенства
. В этом случае с учетом равенства  получим
получим .
.