
|
|
Понятие автомата с магазинной памятью.В отличие от конечных автоматов, автомат с магазинной памятью является набором:
· K — конечное множество состояний автомата · · · Σ — допустимый входной алфавит, из которого формируются строки, считываемые автоматом · S — алфавит памяти (магазина) · Память работает как стек, то есть для чтения доступен последний записанный в неё элемент. Таким образом, функция перехода является отображением Автомат с магазинной памятью может распознать любой контекстно-свободный язык. В чистом виде автоматы с магазинной памятью используются крайне редко. Обычно это модель используется для наглядного представления отличия обычных конечных автоматов отсинтаксических грамматик. Реализация автоматов с магазинной памятью отличается от конечных автоматов тем, что текущее состояние автомата сильно зависит от любого предыдущего. [править]Пример с использованием автомата с магазинной памятью repeat X:=верхний символ магазина; if X - терминал или $ then if X=InSym then удалить X из магазина; InSym:=очередной символ; else error() end else /* X = нетерминал */ if M[X,InSym]=X->Y1Y2...Yk then удалить X из магазина; поместить Yk,Yk-1,...Y1 в магазин (Y1 на верхушку); вывести правило X->Y1Y2...Yk else error() /* вход таблицы M пуст */ end end until X=$ /* магазин пуст */Виды автоматов с магазинной памятью Существуют детерминированные и недетерминированные автоматы с магазинной памятью. Для недетерминированных автоматов (в отличие от детерминированных) существует два эквивалентных критерия завершения работы: 1. пустой магазин 2. достижение конечного состояния Детерминированный автомат завершает работу лишь тогда, когда достигает конечного состояния. Детерминированные МП-автоматы МП-автоматы недетерминированны. Поэтому мы рассмотрим класс детерминированных МП-автоматов, которые в каждой конфигурации могут сделать не более одного такта Детерминированные МП-автоматы очень полезны в задачах компиляции К сожалению, детерминированные МП-автоматы определяют более слабый класс языков, чем КС-грамматики. Приведенные грамматики Эквивалентные преобразования КС-грамматик в предыдущих параграфах позволяют делать следующие три вещи: 1. Сделать грамматику e–свободной. 2. Исключить цепные правила. 3. Исключить бесполезные нетерминалы. Возникает вопрос, можно ли все это сделать одновременно? Грамматика называется приведенной, если она одновременно e–свободна, не имеет цепочных правил и не имеет бесполезных нетерминалов.
Теорема. Каждая КС-грамматика эквивалентна приведенной КС-грамматике. Доказательство. Сначала преобразуем грамматику так, чтобы она не имела бесполезных нетерминалов. Далее, по соответствующему алгоритму предыдущего параграфа преобразуем ее вe–свободную. Вспомним, что согласно этого алгоритма к грамматике добавляется правило A®a1a1, если в нее уже входят правила A®a1Ba1 и B®e. После “насыщения” все e–правила, кромеS®e,удаляются. Если вдруг в полученной грамматике появятся бесполезные нетерминалы, то надо проделать процедуру их удаления. Т.к. она заключается только в выкидывании лишних правил, то грамматика, очевидно, останется e–свободной. Замечание. При применении стандартной процедуры приведения грамматики к e–свободной действительно некоторые нетерминалы могут стать непродуктивными. Проверьте это на следующем примере: S® aB, B®e. Однако нетрудно доказать, что все достижимые нетерминалы останутся достижимыми. Далее рассмотрим два случая. 1. В данной e–свободной грамматике G нет правила S®e. Приводим ее к грамматике без цепочных правил. Вспомним, что в этом случае алгоритм состоит в добавлении правил A®a по уже имеющимся правилам A®Bи B®a. После “насыщения” все цепочные правила удаляются. Ясно, что при этом не появятся e–правила. Если появятся бесполезные нетерминалы, то надо проделать процедуру их удаления. Т.к. она заключается только в выкидывании лишних правил, то цепочных правил не появится. Значит полученная грамматика будет искомой. Замечание. При применении стандартной процедуры удаления цепочных правил некоторые нетерминалы могут стать недостижимыми. Проверьте это на следующем примере: S®aA, A®B,B®a. Однако также, как в доказательстве правильности метода избавления от цепочных правил (см. п. 8) нетрудно показать, что все продуктивные нетерминалы останутся продуктивными. 2. В данной e–свободной грамматике G есть правило S®e. В этом случае прямая процедура избавления от цепочных правил, как в предыдущем пункте, может внести во множество правил новые e–правила и грамматика перестанет быть e–свободной. А процедура избавления от e–правил опять вернуть цепочные (см. пример в конце параграфа). Поэтому надо поступить немного хитрее. Сначала рассмотрим G0 - это G без правила S®e. Проделав для G0 процедуру избавления от цепочных правил, мы получим эквивалентную ейграмматику, в которой нет ни цепочных, ни e–правил. Обозначим и ее за G0. Введем новый нетерминал, допустим A и заменим в G0 все буквы S на этот A. К полученному множеству правил добавим S®e |A. По существу это означает, что мы обозначили через A все непустые слова языка нашей грамматики. Легко видеть, что новая грамматика e–свободна и эквивалентна исходной. Но в ней есть единственноецепочное правило S®A. Еще раз проделаем стандартную процедуру избавления от цепочных правил. Среди правил G0 есть S®a1 |a2 |...|an. Оно превратится в A®b1 |b2 |...|bn, где bi– результат замены в слове ai буквы S на A. Процесс избавления от цепочных правил даст дополнительно S®b1 |b2 |...|bn и ничего больше. Среди этих правил нет ни цепочных, ни e–правил. Выкидываем S®A и получаем искомую грамматику. Пример. Рассмотрим грамматику G: S® e| Ab | b A® SA | S | Ab | b Очевидно, что в G нет бесполезных нетерминалов. Применим процедуру приведения к e–свободной грамматике. Добавляем продукции A® A | e. Других вариантов нет, т.к. A® S, A® bуже имеются. Убрав A® A | e, получим ту же грамматику G. Значит G e–свободна. Попробуем применить к G стандартную процедуру избавления от цепочных правил. Единственное в ней цепочное правило A® S с помощью S® e| Ab | b даст A® e| Ab | b. Новым тут является только A® e. В результате получим грамматику S® e| Ab | b A® SA | e | Ab | b Цепного правила не стало, но появилось новое e–правило A® e ! Применим к этой грамматике процедуру избавления от e–правил. Добавится только одно новое правило A® S и мы вернемся к тому, с чего начали – грамматике G !
Правильная процедура. Рассматриваем грамматику G0 S® Ab | b A® SA | S | Ab | b и избавляемся в ней от цепочных правил. Правило A® S вместе с S® Ab | b дает A® Ab | b, где нет ничего нового. Значит надо просто выкинуть цепочное правило. В результате получим S® Ab | b A® SA | Ab | b Вводим новый нетерминал B, в этих правилах заменяем S на B и добавляем S®e |B. Получим B ® Ab | b A® BA | Ab | b S®e |B . Избавляемся от цепочного правила S®B. В результате добавится S ® Ab | b. Убираем S®B и получаем окончательный результат S ® e |Ab | b B ® Ab | b A® BA | Ab | b
6. Распознаватели для КС-языков. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 где
где — единственно допустимое начальное состояние автомата
— единственно допустимое начальное состояние автомата — множество конечных состояний, причём допустимо F=Ø, и F=K
— множество конечных состояний, причём допустимо F=Ø, и F=K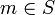 — нулевой символ памяти.
— нулевой символ памяти. . То есть, по комбинации текущего состояния, входного символа и символа на вершине магазина автомат выбирает следующее состояние и, возможно, символ для записи в магазин. В случае, когда в правой части автоматного правила присутствует
. То есть, по комбинации текущего состояния, входного символа и символа на вершине магазина автомат выбирает следующее состояние и, возможно, символ для записи в магазин. В случае, когда в правой части автоматного правила присутствует  , в магазин ничего не добавляется, а элемент с вершины стирается. Если магазин пуст, то срабатывают правила с
, в магазин ничего не добавляется, а элемент с вершины стирается. Если магазин пуст, то срабатывают правила с