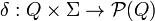|
|
Однозначные и неоднозначные грамматикиРассмотрим некоторую грамматику G({+,–,*,/,(,),a,b},{S},P,S):
Рис. 1.4. Два варианта дерева цепочки a*b+a вывода для неоднозначной грамматики арифметических выражений С точки зрения формального языка, заданного грамматикой, не имеет значения, какая цепочка вывода и какое дерево вывода из возможных вариантов будут построены. Однако в реальных языках структура предложения и его значение (смысл) взаимосвязаны. Это справедливо как для естественных языков, так и для языков программирования. Дерево вывода (или цепочка вывода) является формой представления структуры предложения языка. Поэтому для языков программирования, которые несут смысловую нагрузку, имеет принципиальное значение то, какая цепочка вывода будет построена для того или иного предложения языка. Распознаватели. Общая схема распознавателя Распознаватель (или разборщик) — это специальный автомат, который позволяет определить принадлежность цепочки символов некоторому языку. Задача распознавателя заключается в том, чтобы на основании исходной цепочки дать ответ на вопрос, принадлежит ли она заданному языку или нет. Распознаватели, как было сказано выше, представляют собой один из способов определения языка.
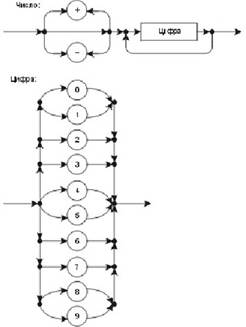
Рис. 1.1. Графическое представление грамматики целых десятичных чисел со знаком
Рис. 1.2. Условная схема распознавателя
ленты, содержащей входную цепочку символов, и считывающей головки, обозревающей очередной символ в этой цепочке; устройства управления (УУ), которое координирует работу распознавателя, имеет некоторый набор состояний и конечную память (для хранения своего состояния и некоторой промежуточной информации); внешней (рабочей) памяти, которая может хранить некоторую информацию в процессе работы распознавателя и, в отличие от памяти УУ, имеет неограниченный объем. чтение очередного символа из входной цепочки; сдвиг входной цепочки на заданное количество символов (вправо или влево); доступ к рабочей памяти для чтения или записи информации; преобразование информации в памяти УУ, изменение состояния УУ. То, какие конкретно операции должны выполняться в процессе работы распознавателя, определяется в УУ. содержимым входной цепочки символов и положением считывающей головки в ней; состоянием УУ; содержимым внешней памяти. Для распознавателя всегда задается определенная конфигурация, которая считается начальной конфигурацией. В начальной конфигурации считывающая головка обозревает первый символ входной цепочки, УУ находится в заданном начальном состоянии, а внешняя память либо пуста, либо содержит строго определенную информацию. Автоматы и конечные автоматы(конспект) Известны два подхода к определению термина автомат. При первом его истолковывают как устройство, которое без непосредственного участия человека выполняет функции приема, преобразования и передачи энергии, информации и т.п. в соответствии с заложенной в него программой, при втором - как математическую модель реальных преобразователей дискретной информации. Функционирование его состоит в том, что последовательность z1,z2,... символов конечного или в общем случае бесконечного алфавита Z, поступающая на вход, вызывает на его выходе определенную последовательность w1,w2,... символов того же или другого алфавита. Таким образом, самой общей математической моделью преобразователя дискретной информации является последовательностная функция, отображающая множество Z всех последовательностей символов алфавита Z в другое множество W* последовательностей символов алфавита W. Такая интерпретация позволяет схематично представить преобразователь как устройство, реализующее отображение одного множества на другое (рис. 2а).
Рис.2а – Формальная модель преобразователя Данное отображение называется алфавитным отображением или алфавитным оператором. Теория автоматов - это раздел теории управляющих систем, изучающий математические модели преобразователей дискретной информации, называемые автоматами. С определенной точки зрения такими преобразователями являются как реальные устройства (вычислительные машины, живые организмы), так и абстрактные системы (например, формальная система – это совокупность абстрактных объектов, не связанных с внешним миром, в котором представлены правила оперирования множеством символов в строго синтаксической трактовке без учета смыслового содержания, т.е. семантики; аксиоматические теории, описывающие определенную совокупность явлений в их причинно-следственной связи друг с другом). Наиболее тесно теория автоматов связана с теорией алгоритмов. Это объясняется тем, что автомат преобразует дискретную информацию по шагам в дискретные моменты времени и формирует результирующую информацию по шагам заданного алгоритма. Эти преобразования возможны с помощью технических и/или программных средств. Автомат можно представить как некоторое устройство (чёрный ящик), на которое подаются входные сигналы и снимаются выходные и которое может иметь некоторые внутренние состояния. При анализе автоматов изучают их поведение при различных возмущающих воздействиях и минимизируют число состояний автомата для работы по заданному алгоритму. Такой автомат называют абстрактным, т.к. абстрагируются от реальных физических входных и выходных сигналов, рассматривая их просто как буквы некоторого алфавита и в связи с идеализированным дискретным временем. При синтезе автоматов (процесс соединения или объединения) формируют систему из элементарных автоматов, эквивалентную заданному абстрактному автомату. Такой автомат называется структурным. Особое место в теории автоматов занимает понятие конечного автомата. Результат преобразования вход => выход (рис.2а) зачастую зависит не только от входа в данный момент времени, но и от того, что было раньше на входе, от входной истории, т.е. от предыстории преобразования. Число возможных входных историй бесконечно (счетно), даже если различных элементов входной информации у автомата конечное число (как в конечном функциональном преобразователе). Чтобы эти предыстории как-то запоминать и отличать друг от друга преобразователь должен иметь память. Для этого в устройство (рис. 1.1,6) вводится алфавит состояний Q = {qx,q2,...qm). Понятие состояния q при этом играет очень важную роль. В своих состояниях автомат запоминает свое концентрированное прошлое. На один и тот же входной сигнал преобразователь может реагировать по-разному в зависимости от того, в каком состоянии он находится в данный момент. Конечный автомат (рис.2б) — математическая абстракция, позволяющая описывать пути изменения состояния объекта в зависимости от его текущего состояния и входных данных, при условии, что общее возможное количество состояний Q и множество входных сигналов Z конечны. Конечный автомат является частным случаем абстрактного автомата.
Рис.2б – Конечный автомат Конечный автомат является одним из важнейших видов управляющих систем. Главным достоинством конечных автоматов является то, что в них естественным образом описываются системы, управляемые внешними событиями. Теория автоматов занимается изучением процессов, протекающих в автоматах различного рода, и общих закономерностей, которым они подчинены, широко применяя для этого алгебраический аппарат, математическую логику, комбинаторный анализ и теорию вероятностей. Теория автоматов находит применение как в математике, так и в решении практических задач. Например, средствами теории автоматов доказывается разрешимость некоторых формальных исчислений. Применение методов и понятий теории автоматов к изучению формальных и естественных языков привело к возникновению математической лингвистики (математическая лингвистика - математическая дисциплина, предметом которой является разработка формального аппарата для описания строения естественных и некоторых искусственных языков.) Понятие автомата может служить модельным объектом в самых разнообразных задачах, благодаря чему возможно применение теории автоматов в различных научных и прикладных исследованиях. Конечный автомат — абстрактный автомат без выходного потока, число возможных состояний которого конечно. Результат работы автомата определяется по его конечному состоянию. Существуют различные варианты задания конечного автомата. Например, конечный автомат может быть задан с помощью пяти параметров: · Q — множество состояний автомата; · q0 — начальное (стартовое) состояние автомата ( · F — множество заключительных (или допускающих) состояний, таких что · Σ — допустимый входной алфавит (конечное множество допустимых входных символов), из которого формируются строки, считываемые автоматом; · δ — заданное отображение множества
(иногда δ называют функцией переходов автомата). Автомат начинает работу в состоянии q0, считывая по одному символу входной строки. Считанный символ переводит автомат в новое состояние из Q в соответствии с функцией переходов. Если по завершении считывания входного слова (цепочки символов) автомат оказывается в одном из допускающих состояний, то слово «принимается» автоматом. В этом случае говорят, что оно принадлежит языку данного автомата. В противном случае слово «отвергается». Конечные автоматы подразделяются на детерминированные и недетерминированные.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|



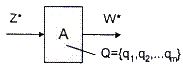
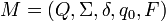 , где:
, где: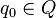 );
); ;
; во множество
во множество 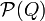 подмножеств Q:
подмножеств Q: