|
|
Уравнение вынужденных колебаний12 Векторная
Модуляция колебаний Модуляцией колебаний называется изменение по определенному закону какого-либо из параметров периодических колебаний (например, амплитуды или частоты), осуществляемое за время, значительно большее, чем период колебаний.
Сложение колебаний Под сложением колебаний понимают нахождение закона результирующих колебаний системы в тех случаях, когда эта система одновременно участвует в нескольких колебательных процессах. Два предельных случая:
В первом случае сложение колебаний сводится к сложению скалярных величин, во втором – к сложению векторных величин.
где x и y – мгновенные значения колебаний; Ax и Ay – амплитуды; w– угловая частота, одинаковая для обоих колебаний; ε – сдвиг фаз между колебаниями.
Уравнение результирующего движения
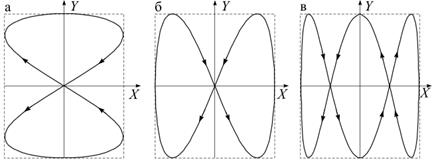
Траектория результирующего движения при сложении взаимно перпендикулярных гармонических колебаний, имеющих циклические частоты (фигуры Лиссажу)
Разложение колебаний
, где – Т -период колебания. Современным инструментом гармонического анализа является быстрое преобразование Фурье (БПФ).
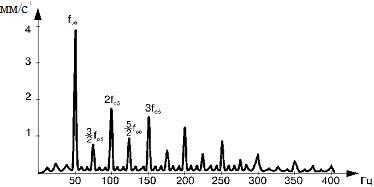
Гармонический анализ ( БПФ) Результатом БПФ является спектр вибрации, который характеризуется набором значений амплитуд, фаз и частот гармонических составляющих. Члены ряда Фурье, соответствующие гармоническим называются первой (или основной), второй, третьей и т. д. гармониками сложного периодического колебания. Совокупность этих гармоник образует спектр колебания. Периодические колебания имеют дискретные (линейчатые) спектры частот. Непериодические колебания имеют непрерывный (сплошной) спектр частот.
Вынужденные колебания Система с одной степенью свободы: • вся масса сосредоточена в одной точке; • движение массы происходит только в плоскости рисунка и только в вертикальном направлении; •
– прогиб под действием прочих сил;
С - жесткость балки.
Уравнение движения системы Принцип Даламбера: уравнения динамики приобретают формальный вид уравнений статики – уравнений равновесия, если в число сил, действующих на систему, кроме приложенных к системе реальных сил, включаются и силы инерции, условно прилагаемые к системе. В процессе движения на систему действуют следующие силы: G – сила веса массы ; Pc – эквивалентная сила неупругого сопротивления, приложенная к массе; Pa – активная внешняя сила, зависящая от времени; Pи – сила инерции.
Уравнение свободных колебаний системы без трения
Частота собственных колебаний с учетом влияния трения:
Уравнение вынужденных колебаний
– относительный коэффициент сопротивления
Коэффициент динамичностипоказывает, как соотносятся между собой амплитуда колебаний системы (динамический прогиб балки) под действием динамической силы с амплитудой P и прогиб балки под действием статической силы, равной по величине P.
Фазовый угол
Если α<<1 фазовый угол практически равен нулю, т. е. сила и прогиб совпадают по фазам (синфазны). При резонансе фазовый угол оказывается близким к π/2, т. е. сила по времени опережает прогиб на четверть периода. При дальнейшем увеличении α разность фаз между силой и прогибом приближается к значению, равному π, т. е. сила и прогиб направлены в противоположные стороны.
Колебания системы с n степенями свободы
где k=1,2,3… – целое число. Формы представляют собой ряд синусоид с одной, двумя, тремя и т. д. полуволнами.
Условие ортогональности Балке с распределенной массой соответствует бесконечное количество собственных частот и главных форм колебаний. Собственные частоты возрастают пропорционально квадрату номера формы: 1: 4: 9: … :n2.
Условие ортогональности главных форм k и l Инерционные силы пропорциональны произведению колеблющихся масс на прогибы, а прогибы в момент максимальных отклонений равны амплитудам. Колебания системы с n степенями свободы Явление резонанса наступает, когда частота вынуждающей силы совпадает с одной из собственных частот системы, а колебания системы при этом происходят преимущественно по соответствующей главной форме, так как прогибы именно по этой форме резко возрастают.Наиболее опасны всегда колебания по низшим формам.
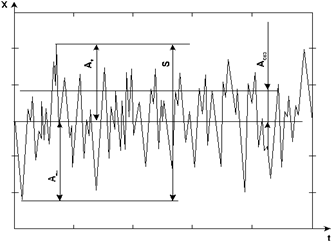
Единицы измерения вибрации
Нормируемые величины Среднеквадратическое значение виброскорости, Vскз=V / 1.4, мм/с Виброперемещение, S, мкм Полигармоническая вибрация В общем случае вибрирующая поверхность совершает колебания, представляющие из себя сумму нескольких гармонических колебаний разных частот, при этом о вибрации говорят как о полигармонической
К чему приводит вибрация?
Вибрационная надежность турбоагрегата Собственной частотой называется любая из частот свободных колебаний
Правило ортогональности (для ротора на жестких опорах)
Жесткость системы «ротор-опоры»
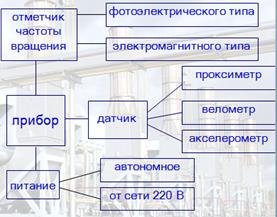
Аппаратура для измерения вибрации
Датчики измерения вибрации Основными характеристиками датчиков являются чувствительность, собственная частота, диапазон измерения виброускорений объекта, рабочий диапазон температур, помехозащищенность и нечувствительность к поперечным составляющим вибрации.
Пъезоэлектрический датчик (пъезоакселерометр) – измеряет виброускорение Велометр – измеряет виброскорость 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 Комплексная
Комплексная
 Амплитудная
Амплитудная Частотная
Частотная Фазовая
Фазовая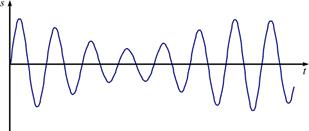
 Сложение колебаний разных направлений
Сложение колебаний разных направлений
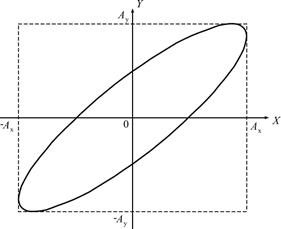
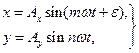 где m и n – относятся между собой как целые числа
где m и n – относятся между собой как целые числа
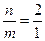
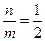

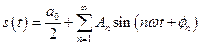 Любое сложное периодическое негармоническое колебание можно представить в виде суммы простых гармонических колебаний
Любое сложное периодическое негармоническое колебание можно представить в виде суммы простых гармонических колебаний с круговыми частотами, кратными основной круговой частоте
с круговыми частотами, кратными основной круговой частоте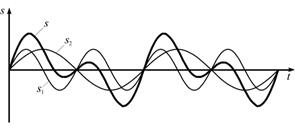

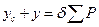 масса балки равна нулю.
масса балки равна нулю.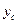
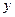 - статический прогиб ;
- статический прогиб ;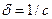 – податливость балки (прогиб под воздействием единичной силы, определяющий упругие свойства балки;
– податливость балки (прогиб под воздействием единичной силы, определяющий упругие свойства балки;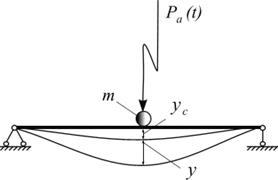 Число степеней свободы - это число независимых величин, через которые может быть определено любое перемещение системы.
Число степеней свободы - это число независимых величин, через которые может быть определено любое перемещение системы.


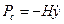
 Уравнение движения в общем виде
Уравнение движения в общем виде

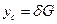 - коэффициент трения
- коэффициент трения - собственная частота системы.
- собственная частота системы. Движение массы представляет собой гармонические незатухающие колебания с круговой частотой w0, называемой собственной частотой системы, и с начальной фазойφ0 .
Движение массы представляет собой гармонические незатухающие колебания с круговой частотой w0, называемой собственной частотой системы, и с начальной фазойφ0 .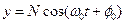 Общее решение уравнения
Общее решение уравнения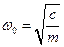
 Уравнение свободных колебаний системы с трением
Уравнение свободных колебаний системы с трением
 Общее решение уравнения
Общее решение уравнения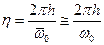
 Темп уменьшения амплитуды при затухающих колебаниях определяется логарифмическим декрементом колебаний (0,05…0,5)
Темп уменьшения амплитуды при затухающих колебаниях определяется логарифмическим декрементом колебаний (0,05…0,5)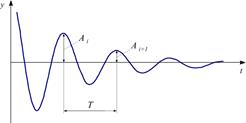

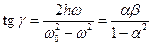
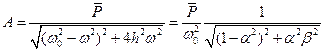
 Частное решение уравнения :
Частное решение уравнения :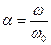

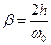 – относительная частота вынуждающей силы;
– относительная частота вынуждающей силы;
 Коэффициент динамичности
Коэффициент динамичности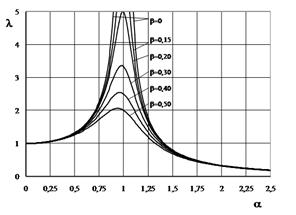 Интенсивный рост амплитуды колебаний по мере приближения частоты вынуждающей силы к собственной частоте системы называется резонансом.
Интенсивный рост амплитуды колебаний по мере приближения частоты вынуждающей силы к собственной частоте системы называется резонансом.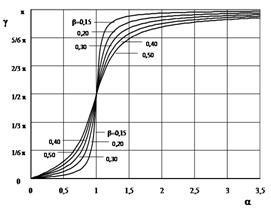
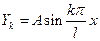 Характеризуются наличием n собственных частот колебаний, каждой из которых соответствует своя форма колебаний. Совокупность амплитуд, соответствующих k-й собственной частоте, образует k-ю главную форму колебаний
Характеризуются наличием n собственных частот колебаний, каждой из которых соответствует своя форма колебаний. Совокупность амплитуд, соответствующих k-й собственной частоте, образует k-ю главную форму колебаний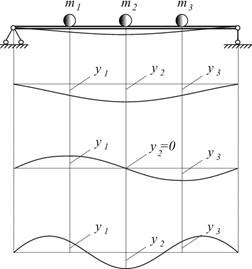
 Между главными формами колебаний существует связь, называемая условием ортогональности. Физический смысл условия ортогональности состоит в том, что работа инерционных сил при колебаниях по одной главной форме на перемещениях по другой главной форме всегда равна нулю. Это означает энергетическую независимость главных форм: переход энергии колебательного движения от одной формы к другой невозможен.
Между главными формами колебаний существует связь, называемая условием ортогональности. Физический смысл условия ортогональности состоит в том, что работа инерционных сил при колебаниях по одной главной форме на перемещениях по другой главной форме всегда равна нулю. Это означает энергетическую независимость главных форм: переход энергии колебательного движения от одной формы к другой невозможен.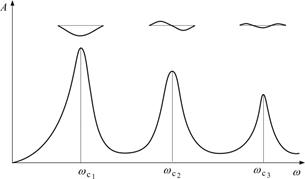
 Виброметрия
Виброметрия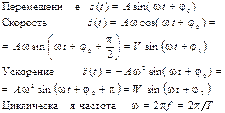

 Вибрация оказывает воздействие на человека и вызывает в зависимости от ее интенсивности: снижение комфорта, производительности труда, возникновение вибрационной болезни
Вибрация оказывает воздействие на человека и вызывает в зависимости от ее интенсивности: снижение комфорта, производительности труда, возникновение вибрационной болезни Критической частотой называется частота вращения, при которой наблюдается максимальный прогиб ротора
Критической частотой называется частота вращения, при которой наблюдается максимальный прогиб ротора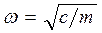
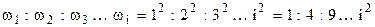
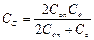
 СОСТАВНЫЕ ЧАСТИ АППАРАТУРЫ
СОСТАВНЫЕ ЧАСТИ АППАРАТУРЫ