
|
|
Результаты численного исследования динамики системы Лоренца12
при σ = 10, β = 8/3. (ρ* ≈ 24.74) 1) 1 ≤ ρ < ρ1 ≈ 13.926.. • т. О – неустойчивая, • точки О1,2 – устойчивые (бистабильность). Зависимость от начальных условий. Две ветви сепаратрисы - Г1 и Г2 Демонстрация динамики
2) ρ1 ≤ ρ < ρ2 ≈ 24.06.. • О1,2 – устойчивые фокусы, • неустойчивые предельные циклы L1 и L2, •B1 (не притягивающее) - колебания между областями притяжения т. О1 и т. О2
3) ρ2 ≤ ρ < ρ* ≈ 24.74… • О1,2 – устойчивые фокусы, области их притяжения ограничены поверхностями L1 и L2 ; • неустойчивые предельные циклы L1 и L2, •B2 - хаотический аттрактор Лоренца, области притяжения – вне L1 и L2
4) ρ* ≤ ρ • т. О и точки О1,2 – неустойчивые неподвижные • притягивающее множество – хаотический аттрактор Лоренца
5) ρ > ρ3 ≈ 148.4 Одно притягивающее множество - предельный цикл (автоколебания). При уменьшении параметра ρ от ρ3 к ρ* переход к хаосу: - через каскад бифуркаций удвоения периода. - через перемежаемость
Предельный цикл в системе Лоренца при σ=10, β = 8/3, ρ =166.
Временная развертка
Зависимости X(t), Y(t), Z(t), полученные для системы Лоренца при σ=16, ρ=28, β=8/3
Мы попытаемся описать имеющиеся представления о появлении и структуре аттрактора в системе Лоренца. Зафиксируем в (1) s = 10, b = 8/3 и будем увеличивать r, начиная с нуля.
При r < 1 система Лоренца имеет асимптотически устойчивую в целом стационарную точку – начало координат. К ней притягиваются все траектории (см. рис. 2). Здесь же отметим, что начальная стадия нашего анализа (вплоть до рис. 4) элементарна и читатель может проделать ее сам. Когда r переваливает через единицу, происходит первая бифуркация. Начало координат теряет устойчивость и от него отделяются две новые устойчивые стационарные точки
и
У линеаризованной в нулевой стационарной точке системы два отрицательных и одно положительноесобственное значение. В соответствии с этим у нулевой стационарной точки есть двумерный входящий ус и одномерный выходящий (см. рис. 3). У линеаризованных в точках X1 и X2 систем все собственные значения отрицательны. При возрастании параметра r пара отрицательных собственных значений этих систем превращается в пару комплексно сопряженных собственных значений. Это, в частности, соответствует тому, что выходящие усыG1 и G2 нулевой стационарной точки начинают закручиваться как спирали около стационарных точек X1 иX2, соответственно (см. рис. 4).
С дальнейшим ростом r стационарные точки X1 и X2 поднимаются выше (они лежат в плоскости x3 = r – 1), а спиралевидные траектории "разбухают". Это происходит до тех пор, пока при r » 13.92 (это значение можно найти только численно) спирали, начинающиеся как выходящие усы нуля, попадают на его входящий ус, образуя две гомоклинические траектории G1 и G2 (см. рис. 5). При возрастании r в этот момент происходит бифуркация гомоклинических траекторий с образованием двухнеустойчивых циклов F1 и F2 (см. рис. 6). Линейные части операторов последования, отвечающих этимциклам, имеют по одному мультипликатору большему единицы и по одному – меньшему единицы, и следовательно, по одному направлению траектории к этим циклам притягиваются, а по другому – отталкиваются. Выходящие усы G1 и G2 нулевой стационарной точки теперь уже не попадают на еевходящий ус (см. рис. 6) – они попадают в области притяжения стационарных точек X2 и X1, соответственно (а не X1 и X2, как было раньше) и закручиваются около них.
При r » 24.06 происходит очередная бифуркация и G1 и G2 попадают на притягивающие многообразия(неустойчивых) циклов F2 и F1 (см. рис. 7). Следующая бифуркация происходит при r = r0 =s(s + b + 3)/(s – b – 1) » 24.74. В этот момент у линеаризованных в точках X1 и X2 систем появляется пара собственных значений на мнимой оси (при r > r0 эти собственные значения имеют положительные вещественные части). Стационарные точки X1 и X2 поглощают неустойчивые циклы F1 и F2, теряя устойчивость (бифуркация Пуанкаре – Андронова – Хопфа). Система жестко возбуждается.
Во время описанного процесса, начиная с r = 13.92 у системы Лоренца появляется предельное инвариантное множество, но до r = r0 оно не является устойчивым, т. е. не притягивает к себе траектории. При r Î (r0,50]это множество L становится "устойчивым". Это и есть собственно аттрактор Лоренца. Представление о том как он выглядит может дать рис. 8, на котором изображена одна траектория системы Лоренца при r = 28:при t® +¥ она стремится к аттрактору. Траектория делает по несколько оборотов то вокруг неустойчивойстационарной точки X1, то вокруг неустойчивой стационарной точки X2, меняя их "случайным образом" (см.рис. 1).
Известно, что аттрактор Лоренца обладает следующими свойствами (обоснование этих свойств к настоящему моменту содержит эмпирические этапы, основанные на результатах численных расчетов). Во-первых, L является аттрактором в том смысле, что существует открытое в R3 множество A такое, чтоL = Çt³0 gtA (здесь gt – оператор сдвига по траекториям системы Лоренца). Другими словами, всетраектории, начинающиеся в A (в данном случае в качестве A можно взять все R3, исключая начало координат), притягиваются к L. Во-вторых, в L имеется всюду плотное множество периодических траекторий, причем каждая из нихнеустойчива. В-третьих, траектории, лежащие в L, экспоненциально разбегаются и поэтому при сколь угодно малом возмущении начальных данных в задаче Коши для системы Лоренца решения на большом интервале времени могут различаться очень сильно. Это делает описываемый системой Лоренца процесс в некотором смысле недетерминированным. В-четвертых, известно, что локально аттрактор Лоренца устроен как произведение канторова совершенного множества на отрезок. Аттракторы, обладающие перечисленными свойствами, обнаружены сейчас во многих динамических системах. Их обычно называют странными аттракторами. С тем, что происходит в системе Лоренца при больших r ясности пока нет. В некоторых интервалах изменения параметра обнаружены устойчивые периодические решения. Интересное явление наблюдается при r Î [210, 234] и r Î [145, 149]. При r = 234 система Лоренца имеет устойчивый цикл, который при уменьшении rиспытывает бифуркацию удвоения периода, теряя устойчивость и порождая устойчивый цикл двойного периода. При дальнейшем уменьшении r новый цикл также теряет устойчивость и от него, в свою очередь, ответвляется цикл двойного периода и т. д. Таким образом, возникает бесконечная последовательность {rk} значений параметра, при котором система Лоренца испытывает бифуркацию удвоения периода. Эта последовательность удовлетворяет недавно открытому закону универсальности Фейгенбаума:
где d = 4.6692... – универсальная постоянная, которая, по современным представлениям, по-видимому, не зависит от конкретной динамической системы, испытывающей бесконечную последовательность бифуркаций удвоения периода.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
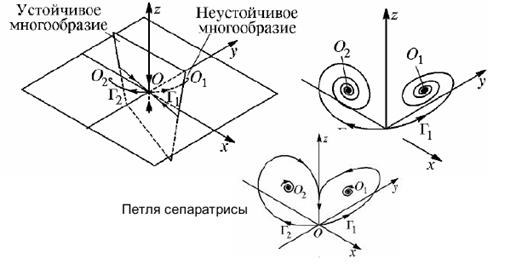
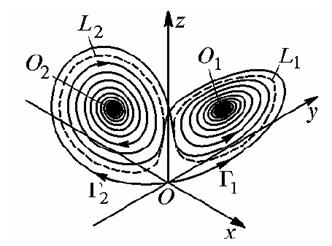
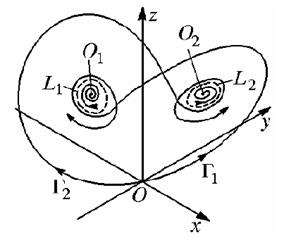
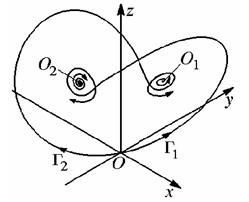
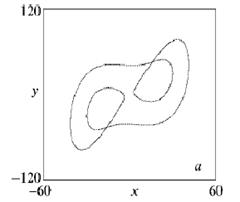
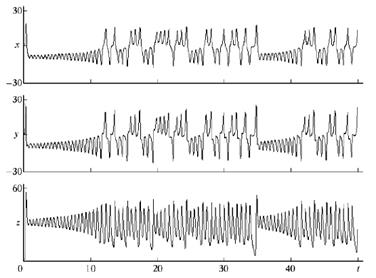
 Рис. 2.
Рис. 2.
 Рис. 3.
Рис. 3.
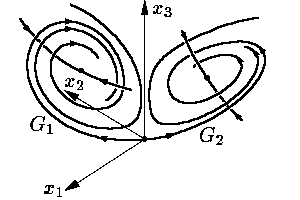 Рис. 4.
Рис. 4.
 Рис. 5.
Рис. 5.
 Рис. 6.
Рис. 6.
 Рис. 8.
Рис. 8.