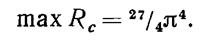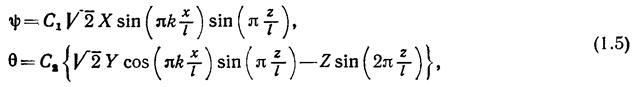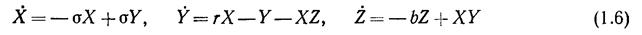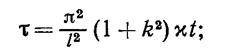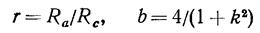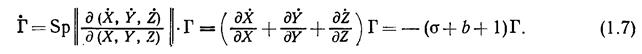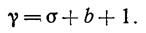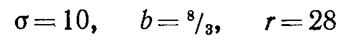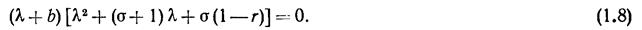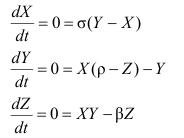|
|
Исследование на неподвижные точки12 Примеры нелинейных динамических систем
1.1.1. Система Ван дер Поля. 1.1.2. Исследование поведения системы. 1.1.3. Бифуркация рождения цикла. 1.1.4. Система Ван дер Поля с периодическим возмущением. 1.4. Система Лоренца. 1.4.1. Вид системы Лоренца 1.4.2. Исследование на неподвижные точки. 1.4.3. Численное исследование динамики системы Лоренца. 1.4.4. Странный аттрактор.
Нелинейная система с предельным циклом (система Ван дер Поля)
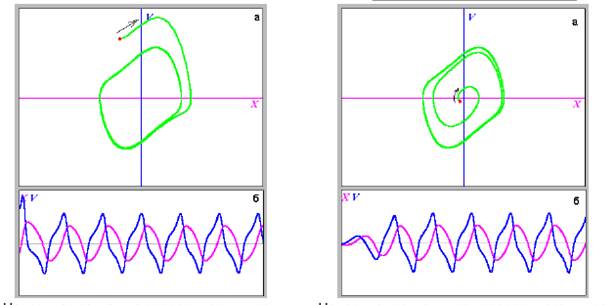
Динамика осциллятора Ван дер Поля при w2 = 2 и c = 1
Предельный цикл – устойчивый режим периодических колебаний в нелинейных системах после завершения переходных процессов
Демонстрация динамики
Примеры решения системы ОДУ Ван-дер-Поля
Покажем применение решателя ОДУ ode15s на ставшем классическим примере – решении нелинейного дифференциального уравнения второго порядка (уравнения Ван-дер-Поля), записанного в виде системы из двух дифференциальных уравнений: y'1 =y2; y'2 = m*(1–y12)*y2–y1 при начальных условиях y1(0)=0; y2(0)=1. Это уравнение описывает колебания в нелинейной системе второго порядка, например в LC-генераторе на электронной лампе или полевом транзисторе, и является классическим примером математического моделирования этих устройств. Поведение системы Ван-дер-Поля существенно зависит от параметра m, который задает степень влияния нелинейности на возникновение и развитие колебаний. При больших m представленная система ОДУ является жесткой. Возьмем значение μ=100. Перед решением нужно записать систему дифференциальных уравнений в виде ODE-функции. Для этого в главном меню выберем File ⇒ New ⇒ MMFile и введем
function dydt = vdp100(t,y) dydt = zeros(2,1); dydt(1) = y(2); dydt(2) = 100*(1 – y(1)^2)*y(2) – y(1);
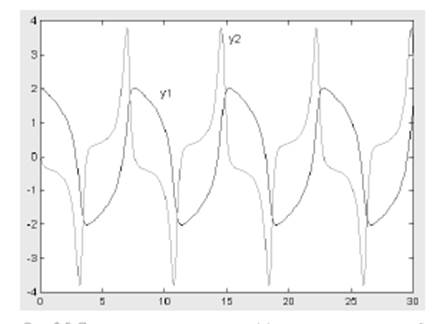
Сохраним данный m-файл-функцию. Тогда решение решателем ode15s и сопровождающий его график (рис. 8.5) можно получить, используя следующие команды:
>> [T,Y]=ode15s(@vdp100,[0 30],[2 0]); plot(T,Y) >> hold on; gtext('y1'), gtext('y2')
Последние команды позволяют с помощью мыши нанести на графики решений y1 = y(1) и y2 = y(2) помечающие их надписи.
Рис. 8.5. Пример решения системы дифференциальных уравнений численным методом
Рассмотрим еще один пример решения уравнения Ван-дер-Поля вида y''1 = 2*(1–y12)*y1–y'1 при m = 2. Оно сводится к следующей системе уравнений: y'1 = y2, y'2 = 2*(1–y12)*y1–y2. Подготовим m-файл ode-функции vdp.m:
function [out1,out2,out3] = vdp(t,y,flag) if nargin < 3 | isempty(flag) out1 = [2.*y(2).*(1-y(2).^2)-y(1); y(1)]; else switch(flag) case 'init' % Return tspan, y0 and options out1 = [0 20];out2 = [2; 0]; out3 = [ ]; otherwise error(['Unknown request ''' flag '''.']); end end
Тогда решение системы с помощью решателя ode23 реализуется следующими командами:
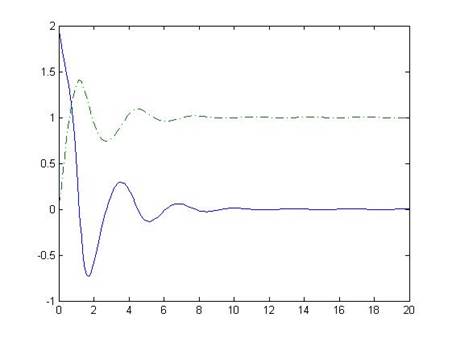
>> [T,Y] = ode23(@vdp,[0 20],[2 0]); >> plot(T,Y(:,1),'-',T,Y(:,2),'-.')
График решения для последнего примера показан на рис. 8.6. Нетрудно заметить, что в данном случае переходные процессы имеют затухающий характер и генерации периодических колебаний нет.
Рис. 8.6. Пример решения системы ОДУ
Бифуркация
Изменение параметра, который называется управляющим, вызывает потерю устойчивости одного состояния (или режима функционирования) системы и переход к другому, качественно отличному от прежнего, состоянию (режиму функционирования). Это явление называется бифуркацией (раздвоением), а значение параметра, при котором это происходит – точкой бифуркации. Графическое отображение зависимости характера поведения системы от параметра, носит название бифуркационной диаграммы.
Бифуркация рождения цикла (бифуркация Хопфа).
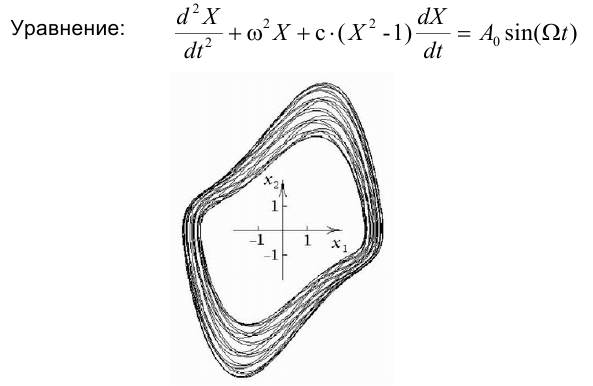
Система Ван дер Поля с периодическим возмущением
Проекция двумерного тора на плоскость переменных x1 = X, x2 = dX/dt.
Система Лоренца
Заславский Г.М., Сагдеев Р.З. ВВЕДЕНИЕ В НЕЛИНЕЙНУЮ ФИЗИКУ: ОТ МАЯТНИКА ДО ТУРБУЛЕНТНОСТИ И ХАОСА. // М.: Наука. гл. ред. Физ.-мат. лит., 1988. – 386 с.
МОДЕЛЬ ЛОРЕНЦА (259)
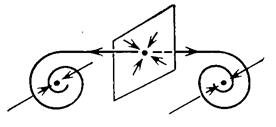
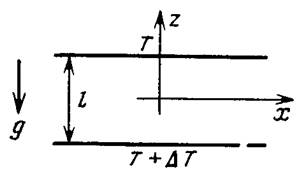
Модель Лоренца появилась в результате целенаправленного поиска некоторых модельных уравнений, которые имели бы непериодические решения стохастического типа. Идея Лоренца заключалась в использовании таких решений для долгосрочного прогноза погоды. Стохастическая динамика, как мы уже знаем, делает бессмысленным какие-либо предсказания на времена, большие времени размешивания. Непредсказуемость обусловлена локальной неустойчивостью траекторий и существованием реальных конечных неточностей в определении начальных условий. Однако макроскопическая динамика усредненных величин на больших временах, сравнимых, например, со временем диффузии, вполне предсказуема (ком. 1). Уравнения модели Лоренца. Физическим процессом, лежащим в основе модели Лоренца, является двумерная тепловая конвекция (рис. 11.1). Она развивается в результате подогревания нижнего слоя под действием градиента температуры и силы тяжести. Подогретая у нижней пластинки жидкость становится легче. Ее вытесняет вверх более холодная и потому более тяжелая жидкость (архимедова сила).
Рис. 11.1. Модель двумерной конвекции (DT > 0)
Далее холодная жидкость, попав вниз, подогревается; теплая, поднявшись вверх, охлаждается. Процесс конвекции описывается двумя уравнениями – уравнением для функции тока y и уравнением теплопроводности для отклонения q температуры от равновесного (линейного по z) закона:
Здесь v – коэффициент вязкости, g – ускорение силы тяжести, a – коэффициент теплового расширения, k – коэффициент температуропроводности, l – расстояние между пластинками, DТ – разница между нижней и верхней температурами (DТ > 0). Обе границы (верхняя и нижняя) предполагаются свободными, и на них y и Рэлей рассмотрел возмущения в системе (1.1) в виде
где k – волновое число возмущения. Он показал [8], что существует некоторое число
такое, что если
то возмущения (1.2) неустойчивы и нарастают. Число Ra называется числом Рэлея. Максимум Rc достигается при k = 1/√2 и равен
Естественно, что весь этот анализ проводился в линейном приближении, и центральный вопрос заключается в том, что представляет собой динамика системы в результате развития неустойчивости. На этот вопрос можно ответить, пользуясь только нелинейной системой, а точнее,– какой-либо разумной аппроксимацией уравнений (1.1). Используя результаты Зальцмана, Лоренц получил аппроксимирующие уравнения следующим образом. Представим y и q в виде
где С1 и С2 – некоторые константы, вид которых далее не потребуется, а X, Y, Z – новые неизвестные переменные, зависящие только от времени. Если подставить (1.5) в (1.1) и отбросить осциллирующие члены, то оказывается, что полученная система уравнений является замкнутой в переменных X, Y, Z. Подобная процедура обрезания тригонометрических сумм для уравнений носит название галеркинской аппроксимации. Существенно, что в данном случае вид нелинейности системы (1.1) порождает единственную аппроксимацию с системой уравнений минимального порядка. Она имеет вид
и называется системой Лоренца. В ней точка означает дифференцирование по безразмерному времени
s = v/k – число Прандтля,
(ком. 2). Физический смысл переменных X, Y, Z очевиден из определений (1.5). Величина X пропорциональна скорости конвекции, Y – разности температур между восходящим и нисходящим потоками, Z пропорционально отклонению вертикального профиля температуры от линейного. Фазовое пространство системы (1.6) трехмерно, и она имеет число степеней свободы N = 3/2. Изменение фазового объема Г со временем определяется выражением
Отсюда видно, что объем фазовой жидкости стремится к нулю экспоненциально с показателем
Кроме того, второе равенство в (1.7) также указывает на сжимаемость фазовой жидкости. Если при этом траектории не выходят из сжимающегося объема, то существует некоторое предельное множество – аттрактор – с нулевым фазовым объемом, к которому притягиваются траектории при t → ∞. Аттрактор может быть обычным (например, предельным циклом), но может быть и стохастическим. Последнее и было обнаружено Лоренцем при
(рис. 11.2). Значение b соответствует k2 = 1/2 т. е. максимальному инкременту. Критическое число для неустойчивости стационарной конвекции (см. ниже) равно при этом r ≈ 24,74. Поэтому r = 28 означает слабую надкритичность. Линеаризация. Система Лоренца зависит от нескольких параметров, и поэтому исследование ее динамики является достаточно сложной задачей. Тем не менее усилиями многих исследователей стало ясно, как возникает стохастический аттрактор. Эти результаты начинаются с работы самого Лоренца. Простейшая операция, с которой следует начать, заключается в определении критических точек в фазовом пространстве. Линеаризация системы (1.1) в окрестности стационарного решения X = Y = Z = 0 приводит к характеристическому уравнению
При r > 0 уравнение (1.8) имеет три действительных корня. В области
все корни l < 0, и решения устойчивы. В этом случае имеется единственный аттрактор, которым является неподвижная точка в начале координат. Ей соответствует стационарная теплопроводность Рэлея – Бенара.
Однако при r > 1 возникает один положительный корень. Он вызывает развитие неустойчивости и связанной с ней конвекции. Критическое значение rc = 1 как раз соответствует критическому числу Рэлея. Переход через r = 1 сопровождается потерей устойчивости аттрактора в начале координат. Появляются две новые неподвижные точки с координатами
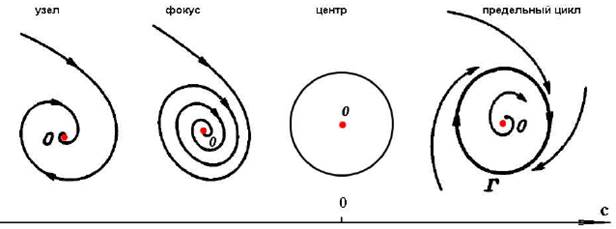
Последовательность бифуркаций. В точке r = 1 происходит первая бифуркация в модели Лоренца. Ее легче понять, обратившись к рис. 11.3 и 11.4. В области (1.9) все траектории притягиваются к началу координат. Поэтому говорят, что все траектории образуют устойчивое многообразие начала координат. При r > 1 (рис. 11.4) ответвляются два устойчивых положения равновесия (1.10). Появляется неустойчивое многообразие начала координат. С дальнейшим ростом r два собственных значения l становятся комплексно сопряженными. Им соответствуют две спирали на рис. 11.5, а точкам притяжения спиралей – стационарная конвекция Рэлея – Бенара.
Рис. 11.5. Появление спиралей при r > 1
Дальнейший рост г приводит к увеличению диаметра спиралей, пока они не коснутся друг друга. Это происходит при r ≈ 13,926 (рис. 11.6). В результате этой бифуркации образуется гомоклиническая траектория. При r > 13,926 происходят еще некоторые бифуркации и появляются квазистохастические траектории. Мы не будем их описывать и перейдем сразу к бифуркации при r ≈ 24,74. Аттрактор Лоренца. Две устойчивые точки в центрах спиралей превращаются в неустойчивые. В результате при r > 24,74 траектория, приблизившись к одной из них, «оттолкнется» от нее и начнет путь ко второй точке (рис. 11.7). Там произойдет то же отталкивание. Возникает случайное блуждание траектории между двумя неустойчивыми точками. При этом вокруг каждой из них траектория совершает некоторое число оборотов (ср. с рис. 11.2). В пределе возникает стохастический аттрактор Лоренца.
Если не быть слишком точным в определениях, то можно сказать, что любая траектория спустя какое-то время притягивается и «садится» на некоторую область в фазовом пространстве. Область устроена сложно и имеет канторову структуру. Движение на ней является стохастическим (точнее, в очень малой окрестности вблизи этой области, так как она является предельной для траектории). Описанная предельная область и является аттрактором Лоренца. Исследование модели Лоренца показало, прежде всего, что новое понятие стохастического аттрактора может быть связано с понятием турбулентности. Действительно, модель Лоренца слишком проста, для того чтобы не ожидать стохастичности в значительно более сложных системах. Кроме того, бифуркационный анализ ее показал, что иногда существует реальная возможность построить «бифуркационное дерево», указывающее последовательность различных метаморфоз с решениями в пространстве параметров системы. Таким образом, казалось бы, можно искать путь появления турбулентности, или, иначе, построить сценарий ее развития. Мы еще остановимся, на этом вопросе более подробно в конце главы. Здесь лишь отметим главную особенность модели Лоренца, значительно ограничивающую возможности ее сравнения с реальными экспериментальными данными. Она связана, конечно, с обрезанием системы уравнений. Задача с очень большим числом степеней свободы заменена задачей с минимальным их числом. Волновое число фактически входит в систему Лоренца как параметр. Тем самым исключаются из рассмотрения всевозможные структурные элементы движения жидкости. В действительности эта сторона динамики чрезвычайно богата [10], и мы приведем в следующем параграфе небольшую информацию о структурной эволюции конвекции при переходе к турбулентности (ком. 3).
КОММЕНТАРИИ 1. Уравнения модели Лоренца [1] появились в результате упрощения системы Зальцмана [2] для описания конвекции конечной амплитуды. Существует большое число работ, посвященных ее математическим и численным исследованиям. Укажем на некоторые из них [3-6]. Сам Лоренц обнаружил стохастичность и описал ряд ее свойств. Различные приложения модели Лоренца для долгосрочного прогноза погоды имеются в книге [7]. 2. Метод Галеркина обладает определенными достоинствами при анализе двумерной гидродинамики. Используемая аппроксимация точно удовлетворяет граничным условиям и сходится к точному решению для широкого класса внешних возмущений. Эти его качества дополняются удобством проведения вычислений. 3. Модель Лоренца, не описывая многих принципиальных особенностей турбулентного движения среды, тем не менее, важна, как такой пример динамической системы, иа котором можно проследить различные этапы эволюции и бифуркаций. Качественный анализ многомерных систем является очень сложным. Модель Лоренца явилась своеобразным генератором реально возможных бифуркаций. Система уравнений, подобных (1.6), может встречаться в различных физических задачах, в которых ведущим является трехмодовое взаимодействие.
1. Lorenz Е. N. // J. Atmosph. Sci. – 1963. – V. 20. –P. 130. 2. Saltsman В. // J. Atmosph. Sci. – 1962. – V. 19. – P. 329. 3. Kaplan J. L., Yorke A. // Comm. Math. Phys. – V. 67, № 2. – В.: Springer-Verlag, 1979. 4. Афраймович В. С, Быков В. В., Шильников Л. П. // Докл. АН СССР. – 1977.– Т. 234. – С. 336. 5. Williams R. F. The structure of Lorenz Attractors. Lecture Notes in Mathematics, 615. – В.: Springer-Verlag, 1977. – P. 94. 6. Бунимович Л. А., Синай Д. Г. Стохастичность аттрактора в модели Лоренца // Нелинейные волны. – М.: Наука, 1979. – С. 212. 7. Сонечкин Д. М. Стохастичность в моделях общей циркуляции атмосферы.– Л.: Гидрометеоиздат, 1984. 8. Rayleigh // Phil. Mag. – 1916. – V. 32. – P. 529. 9. Lanford О. // Turbulence Seminar / Eds. Bernard, Rativ. – Springer Lecture Notes in Mathematics. – 1977. – V. 615. – P. 114. 10. Cellular Structures in Instabilities. Lecture Notes in Physics. 210 / Eds J. E. Wesfreid and S. Zaleski. – В.: Springer–Verlag, 1984.
Исследование на неподвижные точки
1. X = Y = Z = 0 - точка О = (0,0,0) всегда является неподвижной. 2. условие стационарности:
ещё две неподвижные точки О1,2 (но не всегда устойчивые): Zст = ρ -1, Xст = Yст = ± Ö(βZст) = Ö(β(ρ −1)).
Анализ устойчивости неподвижных точек:
• при ρ < 1 т. О - устойчивый узел, других устойчивых точек нет. Это означает отсутствие конвекции, • при 1 < ρ < ρ* = σ(σ + β + 3)/(σ - β -1). Появляются две новые устойчивые точки О1,2, если σ > β-1. Точка при этом О - становится неустойчивой. Два возможных направления вращения в конвективной ячейке, т.е. два устойчивых динамических режима. • при ρ > ρ* точки О, О1,2 становятся неустойчивыми. Это означает отсутствие регулярных устойчивых режимов в системе и переход к хаотической конвекции.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
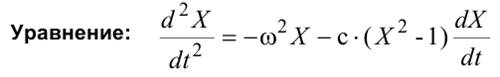


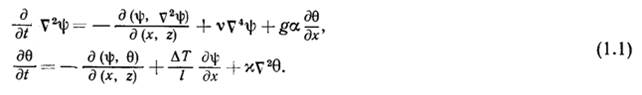
 y обращаются в нуль.
y обращаются в нуль.