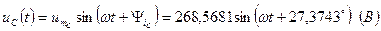|
|
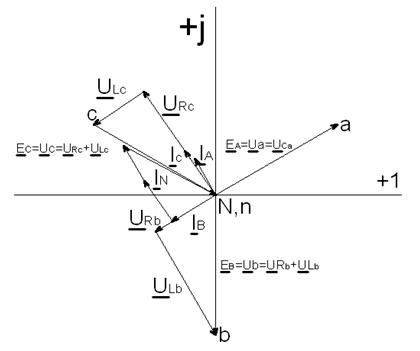
Строим векторную диаграмму токов и топографическую диаграмму напряжений.12 Для построения топографической диаграммы вычисляем действующие значения напряжений элементов схемы:
Предполагая, что точка N имеет нулевой потенциал, помещаем ее в начало координат на комплексной плоскости (Рисунок). Выбираем масштабы по току и напряжению:
Рисунок 2.5. Векторная диаграмма токов и топографическая диаграмма напряжений при отсутствии нейтрального провода.
2.4. Определяем показания ваттметров: а) путем вычисления комплексных мощностей; б) пользуясь диаграммами п.3. Сравнить сумму показаний ваттметров с мощностью, выделяемых в резисторах цепи. Обмотка по напряжению ваттметра
Алгебраическая сумма показаний ваттметров:
Мощность, рассеиваемая резисторами в цепи:
т.е. по показаниям двух ваттметров можно определить активную мощность цепи.
Показания ваттметров можно определить, пользуясь диаграммами (рис. 2.5). Для этого находим углы, составляемые векторами
Относительная ошибка определения активной мощности цепи с помощью диаграмм:
т.е. достаточно малая. 5) Построим временные графики напряжения и тока, относящихся к одному из ваттметров, и укажем угол сдвига фаз. Электрические величины, относящиеся к первому ваттметру, - это напряжение Аналогично находим для тока
Временные графики величин
   
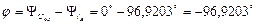 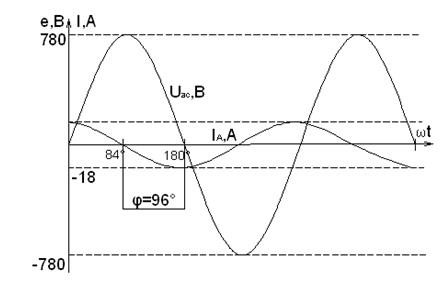
Рисунок 2.6. Временные графики величин 6) Считая узлы n и N закороченными, произведем расчет полученной схемы, определим показания ваттметров W1 и W2. При закорачивании узлов n и N комплексы токов в ветвях находим, пользуясь законом Ома:
Для определения показаний ваттметров находим соответствующие комплексные мощности: Сумма показаний ваттметров:
Мощность, рассеиваемая на резисторах :
т.е. 7) Полагая, что в цепь включены три ваттметра (рис. 2.7), определим их показания и произведем анализ, аналогичный п.4. Активную мощность цепи можно измерить с помощью трех ваттметров, схема включения которых приведена на рис. 2.7. Убедимся в этом:
Рисунок 2.7. Схема электрическая принципиальная. 8) Построим векторную диаграмму токов и топографическую диаграмму напряжений для схемы

Рисунок 2.8. Схема электрическая принципиальная. На рис. 2.8 изображена комплексная схема замещения цепи, расчет которой проведен в п.6. Находим действующие значения напряжений элементов:
Так как точки n и N закорочены, то их потенциалы одинаковы. Принимаем эти потенциалы равными нулю и помещаем точки n и N в начало координат на комплексной плоскости (рис. 2.9).
Рисунок 2.9. Векторная диаграмма токов и топографическая диаграмма напряжений при наличии нейтрального провода.
Рисунок 2.10. Схема электрическая принципиальная.
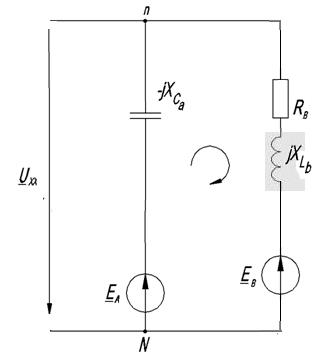
Рисунок 2.11. Схема электрическая принципиальная.
Записываем уравнение по 2-ому закону Кирхгофа для входного контура:
Тогда
Вычисляем эквивалентное сопротивление:
Комплекс тока находим по схеме рис. 2.10 на основании закона Ома:
что совпадает с найденными в п.2 значениями. Отсюда находим :

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
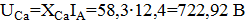
 откуда заключаем, что к конденсатору приложено огромное напряжение:
откуда заключаем, что к конденсатору приложено огромное напряжение: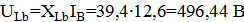
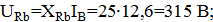




 находится под напряжением, комплекс которого
находится под напряжением, комплекс которого  , а по токовой обмотке протекает ток, комплекс которого
, а по токовой обмотке протекает ток, комплекс которого  . Находим комплексную мощность
. Находим комплексную мощность  :
: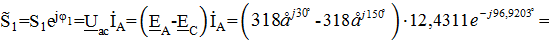

 Аналогично получаем значение мощности:
Аналогично получаем значение мощности:

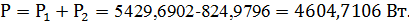

 и
и 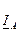 векторами
векторами  и
и  . Измерения транспортиром дают следующие результаты:
. Измерения транспортиром дают следующие результаты:  ;
; 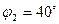 . Измерения линейкой длин векторов дают действующие значения соответствующих напряжений и токов:
. Измерения линейкой длин векторов дают действующие значения соответствующих напряжений и токов:

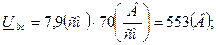
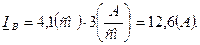
 Вычисляем активные мощности:
Вычисляем активные мощности: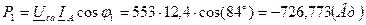 ;
; ;
; .
.
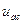 и ток
и ток 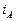 . Так как
. Так как  то амплитуда этого напряжения:
то амплитуда этого напряжения:  и начальная фаза
и начальная фаза 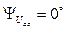 .
.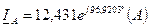 :
: ,
,  .
. и
и 

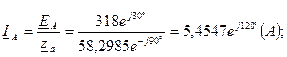
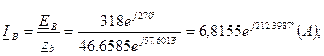
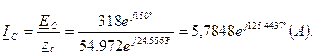
 Действующее значение тока
Действующее значение тока 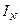 , протекающего в проводе, соединяющем узлы n и N:
, протекающего в проводе, соединяющем узлы n и N:
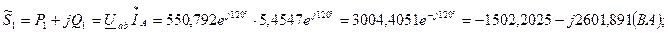

 .
.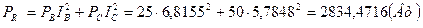 ,
,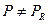 , из чего делаем вывод – с помощью двух ваттметров невозможно определить активную мощность цепи с закороченными узлами n и N.
, из чего делаем вывод – с помощью двух ваттметров невозможно определить активную мощность цепи с закороченными узлами n и N.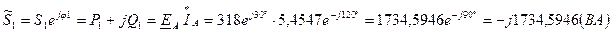
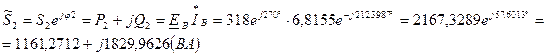
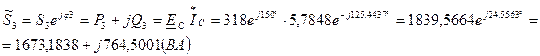
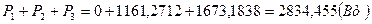
 т.е. сумма показаний трех ваттметров равна мощности рассеиваемой на резисторах (см. п.6).
т.е. сумма показаний трех ваттметров равна мощности рассеиваемой на резисторах (см. п.6).

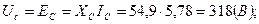
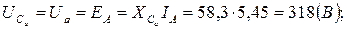

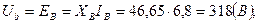
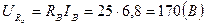 ;
;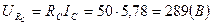 .
. 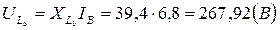
 9) Вычислить ток
9) Вычислить ток 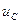 для схемы рис. 2.3 методом эквивалентного генератора. Выделяем ветвь схемы с исковым током, а оставшуюся часть схем представляем эквивалентным генератором с параметрами
для схемы рис. 2.3 методом эквивалентного генератора. Выделяем ветвь схемы с исковым током, а оставшуюся часть схем представляем эквивалентным генератором с параметрами 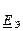 и
и  (рис. 2.10).
(рис. 2.10).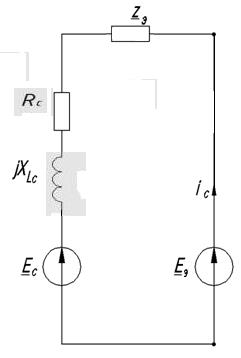
 Для определения этих параметров находим комплекс напряжения холостого хода
Для определения этих параметров находим комплекс напряжения холостого хода  активного двухполюсника (рис. 2.11) и его комплексное сопротивление относительно точек n и N. При этом
активного двухполюсника (рис. 2.11) и его комплексное сопротивление относительно точек n и N. При этом  =
= 
 Откуда
Откуда 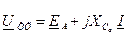
 Находим комплекс тока:
Находим комплекс тока:

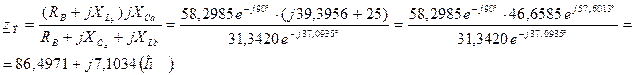


 ,.
,.