
|
|
Надежность теста. Теория надежности.Надежность одно из основных понятий психодиагностики и, вместе с тем, одно из самых сложных. К.М. Гуревич отмечает «Надежность - крайне сложное и многоплановое понятие, одна из основных функций которого - оценить постоянство показателей тестовых испытаний. В принципе можно сказать, что надежность должна обосновывать ошибку измерения - она должна показывать, какая часть изменчивости показателей ошибочна» [17, стр. 27]. На практике понятие "надежности" имеет два значения: одно связано с воспроизводимостью результатов тестирования, другое – с внутренней согласованностью теста [8]. На понятии "надежность" основывается вычисление "ошибки измерения", с помощью которой определяются вероятные пределы колебания измеряемой величины, возникающей под воздействием случайных факторов. Можно сказать, что в широком смысле слова надежность теста показывает, в какой мере индивидуальные различия в тестовых результатах являются «истинными», а в какой мере они могут быть отнесены к случайным ошибкам. Надежность это помехоустойчивость теста, независимость его результатов от действия всевозможных случайных факторов. К числу таких факторов следует отнести: - разнообразие внешних материальных условий тестирования (время суток, освещенность, температура, наличие посторонних звуков и т.п.); - динамичные внутренние факторы, по-разному действующие на разных испытуемых в ходе тестирования (настроение, утомление, другие особенности состояния испытуемого); - информационно-социальные факторы (контакт с психологом, наличие других людей, сама ситуация тестирования и пр.). Разнообразие и изменчивость этих факторов так велики, что они обусловливают появление у каждого испытуемого непрогнозируемого по размеру и направлению отклонения измеренного тестового балла (т.е. такого, который можно было бы получить в идеальных условиях). Поэтому, общий разброс (дисперсию) результатов произведенных измерений можно представить как результат суммы двух источников разнообразия: самого измеряемого свойства и нестабильности измерительной процедуры, обусловливающей наличие ошибки измерения. Это нашло свое выражение в классической формуле, описывающей надежность теста в виде отношения истинной дисперсии к дисперсии эмпирически зарегистрированных баллов [1, 13, 15, 16]:
α = 1 - где: α- надежность теста;
Итак, эта формула читается так: надежность теста равняется единице минус отношение дисперсии ошибки к дисперсии эмпирически зарегистрированных баллов. Из этой формулы получаем, что стандартная ошибка измерения равна: В общем случае можно сказать, что ошибку измерения в психометрике определяют с помощью корреляционных методов, которые дают возможность оценить надежность (или, что одно и тоже точность) через устойчивость и согласованность результатов, полученных как на уровне целого теста, так и на уровне отдельных его пунктов. Рассмотрим вначале надежность теста, связанную с воспроизводимостью результатов тестирования – так называемую, "ретестовую" или "диахронную" надежность. Затем, проанализируем понятие "надежности", связанное с внутренней согласованностью теста. В завершении этого параграфа проанализируем критический взгляд на такие понятия, как "ретестовая надежность ", "синхронная надежность" и достаточно подробно остановимся на "теории надежности", позволяющей психологу, разрабатывающему или использующему тест, понять всю важность данного параметра теста. 1. Ретестовая (диахронная) надежность (надежность теста, как целого). Самый естественный способ определить надежность результатов теста - использовать тот же тест второй раз. В этом случае коэффициент надежности просто равен корреляции между двумя результатами, полученными на одних и тех же испытуемых в каждом из двух случае проведения теста. Приводя в руководстве к тесту его ретестовую надежность, всегда следует указывать, в каком интервале времени она измерена. Как правило, выбирают этот интервал исходя из следующих соображений. На дисперсию ошибки тестовых результатов обычно влияют случайные колебания с периодом от нескольких часов до нескольких месяцев. Поэтому, определяя тип тестовой надежности, стараются придерживаться небольших временных интервалов. (Например, при тестировании маленьких детей этот период должен быть еще короче, чем у взрослых испытуемых, поскольку в раннем детстве возрастные изменения происходят в течение месяца и даже быстрее.).
В целом для любого типа испытуемых интервал между двумя последовательными применениями теста обычно не должен быть меньше двух недель и превышать 6 месяцев [1]. Следует учесть, что данное понятие надежности в основном характеризует выполнение теста самого по себе, а не тестируемую область поведения (т.е. характеризует стабильность теста, как измерительного инструмента). В качестве коэффициента корреляции для этого типа надежности обычно подсчитывают известный коэффициент корреляции произведения моментов Пирсона [1, 15]:
r -коэффициент корреляции между результатами двух тестовых испытаний;
∑ -сумма произведения отклонений от средних значений каждого испытуемого в первом и втором испытаниях; N- число испытуемых. Оценка значимости этого коэффициента производится следующим образом: - вычисляется квадратическая ошибка коэффициента корреляции по формуле
при малом числе наблюдений n берется "числом степеней свободы", обычно как n-2, и ошибка коэффициента корреляции вычисляется так
Ошибка коэффициента корреляции приближается к нулю, когда коэффициент корреляции приближается к единицы. Таким образом, при r =1 независимо от знака, mr =0. Значение коэффициента корреляции оценивается с помощью критерия достоверности, который представляет отношение этого коэффициента к своей средней квадратической ошибке, т.е.
Далее полученный критерий достоверности (t) сравнивается с табличным (см. приложение 2). Напомним из статистики, что если необходимо оценить достоверность различий, наблюдаемых между двумя коэффициентами корреляции, формула для расчета критерия достоверности принимает вид
Знание надежности теста позволяет уточнить "истинное" значение тестового балла индивида, применяя формулу:
r - эмпирическая надежность теста; Например, что испытуемый получил балл IQ по шкале Стенфорд-Бине равный 120 нормализованным очкам, Все выше сказанное касалось тестовс интервальными шкалами, для шкал порядка в качестве меры ретестовой надежности используется ранговый коэффициент корреляции Спирмена:
Оценка значимости коэффициента корреляции Спирмена производится аналогичным образом через расчет квадратической ошибки по формуле
Теперь проанализируем понятие "надежности", связанное с внутренней согласованностью теста, и которое находит свое выражение в таких понятиях, как "одномоментная" или "синхронная" надежность. 2. Одномоментная (синхронная) надежность (согласованность).Этот тип надежности независим от устойчивости (поскольку не имеет временного интервала) и имеет особую содержательную и операциональную природу. Ее надо понимать именно как согласованность частей теста. В психотехнике этот вид надежности часто называют коэффициентом внутренней согласованности теста. Для того, чтобы ее измерить следует скоррелировать между собой параллельные формы теста. Особо отметим, что проводится только однократное применение теста (а уже потом его искусственно разбивают на две параллельные формы). Чаще всего параллельные формы теста получают расщеплением составного теста на "четную" и "нечетную" половины: к первой относятся все четные пункты заданий теста, ко второй - соответственно, все нечетные. По каждой половине рассчитываются суммарные баллы и между двумя рядами баллов подсчитываются допустимые коэффициенты корреляции [1, 15]. Если параллельные формы тесты не нормализованы, то предпочтение отдается ранговой корреляции. При подобном расщеплении получается коэффициент корреляции, относящийся к половинам теста. Для того, чтобы найти надежность(согласованность) целого теста, пользуются формулой Спирмена-Брауна:
Следует отметить, что делить тест на две части можно разными способами, и каждый раз получаются несколько разные коэффициенты; поэтому в психометрике предложен способ оценки синхронной надежности, который соответствует разбиению теста на такое количество частей, сколько в нем отдельных пунктов. В этом случае, синхронную надежность теста можно оценить с помощью формулы Кронбаха:
α-коэффициент Кронбаха; k-количество пунктов (заданий) теста;
В 1957 году Дж. Китс предложил следующий критерий для оценки статистической значимости коэффициента α(1):
k - количество пунктов; n - количество испытуемых; α - надежность. Вычисленная статистика Как видно, формула Кронбаха позволяет оценить взаимную согласованность пунктов теста, используя только подсчет дисперсий (вся важность этой формулы для психометрики станет понятна после анализа теории надежности). Коэффициент αпозволяет также оценить и среднюю корреляцию между i-тым и j-тым произвольными пунктами теста, так как он связан с этой средней корреляцией следующей формулой: α = где Из всего вышесказанного вытекает возможность повысить синхронную надежность теста, увеличивая численность пунктов теста (в k раз). Из формулы видно, что при больших k малое значение r - может сочетаться с высокой надежностью (например: пусть r = 0,1,аk= 100,тогда согласно формуле (***) имеем: α = 0,91). При прочих равных условиях, чем больше заданий содержит тест, тем выше его надежность. Все приведенные формулы относятся к оценке надежности одномерного теста, направленного на измерение одной характеристики. Перейдем теперь к обсуждению "теории надежности" тестов [10], опираясь на понятия изложенные выше. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 -дисперсия ошибки;
-дисперсия ошибки; -дисперсия теста.
-дисперсия теста. . Можно сказать, что величина ошибки измерения - обратный индикатор точности измерения: чем выше ошибка, тем шире диапазон неопределенности на шкале (доверительный интервал), внутри которого оказывается статистически возможной расположение истинного балла данного испытуемого [15].
. Можно сказать, что величина ошибки измерения - обратный индикатор точности измерения: чем выше ошибка, тем шире диапазон неопределенности на шкале (доверительный интервал), внутри которого оказывается статистически возможной расположение истинного балла данного испытуемого [15]. ,где
,где -эмпирическая дисперсия первого испытания;
-эмпирическая дисперсия первого испытания; - эмпирическая дисперсия второго испытания;
- эмпирическая дисперсия второго испытания; ;
; ;
; ;
; .
. , где
, где -истинный балл;
-истинный балл; -эмпирический балл i-го испытуемого;
-эмпирический балл i-го испытуемого; -среднее для теста;
-среднее для теста; ,где
,где 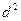 - разность рангов i-го испытуемого в первом и втором ранговом ряду (1, 4).
- разность рангов i-го испытуемого в первом и втором ранговом ряду (1, 4). ;
; , где
, где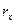 - эмпирически рассчитанная корреляция для половин;
- эмпирически рассчитанная корреляция для половин; - надежность целого теста.
- надежность целого теста. ,где
,где - дисперсия по i-му пункту теста;
- дисперсия по i-му пункту теста; , где
, где - эмпирическое значение статистики χ2 с п-1 степенью свободы;
- эмпирическое значение статистики χ2 с п-1 степенью свободы; , (***)
, (***) - средняя корреляция между пунктами теста.
- средняя корреляция между пунктами теста.