
|
|
Перечень основных показателей вариабельности сердечного ритма
Упражнения 1. Найти вероятность выпадения грани с четным номером при однократном бросании игрального кубика. 2. Найти вероятность извлечения зеленого шара при извлечении одного шара наугад из корзины, содержащей 4 зеленых шара и 6 белых. 3. На столе находятся 5 ампул с препаратом А, 10 — с препаратом В и 15 - с препаратом С. Наугад берут одну ампулу. Какова вероятность того, что выбранная ампула окажется ампулой с препаратом В? 4. В студенческой группе 6 юношей и 9 девушек. Какова вероятность того, что наугад вызванный студент окажется юношей? 5. Из 10 000 упаковок некоторого препарата, выпущенных фармацевтической фабрикой за день, случайным образом отобраны 100 упаковок, и среди них обнаружены 3 бракованные. Найти относительную частоту появления бракованных упаковок среди отобранных и оценить вероятность того, что упаковка, наугад выбранная из всех выпущенных в этот день, окажется бракованной. 6. Студенты первого курса сдавали экзамен по биологии. Среди 40 наугад выбранных студентов оказалось 10 студентов, сдавших экзамен на «отлично». Найти относительную частоту появления студентов, отлично сдавших экзамен, среди выбранных студентов и оценить вероятность того, что студент, наугад выбранный из всех студентов, сдававших экзамен, сдал его на отлично. 7. В ящике находятся 4 ампулы с препаратом А, 6 — с препаратом В и 10 — с препаратом С. Какова вероятность того, что выбранная наугад ампула окажется ампулой с препаратом А или В? 8. В группе из 15 студентов 5 сдали коллоквиум по органической химии на «отлично» и 6 — на «хорошо». Какова вероятность того, что наугад выбранный из этой группы студент сдал коллоквиум на «хорошо» или «отлично»? 9. Аптека получила 100 упаковок некоторого лекарственного препарата со склада № 1, 200 - со склада № 2 и 500 — со склада № 3 . Какова вероятность того, что очередная проданная упаковка поступила со склада № 1 или № 2? 10. Найти вероятность того, что при двух последовательных подбрасываниях монеты оба раза выпадет герб. 11. Вероятность осуществления некоторой химической реакции при проведении химического эксперимента определенного вида равна 0,9. Найти вероятность того, что данная реакция произойдет в двух последовательно проведенных экспериментах. 12. Вероятность поражения цели первым стрелком равна 0,90, вторым — 0,95. Найти вероятность того, что оба стрелка не промахнутся, если произведут по одному выстрелу. 13. В коробке находятся 4 ампулы с препаратом А и 10 — с препаратом В. Какова вероятность того, что две последовательно выбранные ампулы окажутся ампулами с препаратом А? 14. Из 12 студентов 3 не прошли профилактический осмотр. Найти вероятность того, что оба из 2 случайным образом выбранных из этой группы студентов не прошли осмотр. 15. Принимая вероятность появления мальчика при рождении ребенка равной 0,5, найти вероятность того, что в семье с 6 детьми: а) мальчиков нет; б) 4 мальчика; в) все дети — мальчики. 16. Вероятность осуществления некоторой химической реакции при проведении эксперимента определенного вида равна 0,8. Найти вероятность того, что данная реакция произойдет в двух из семи проведенных экспериментов. 17. Вероятность заболевания гепатитом для жителя некоторой области в определенный период года составляет 0,0005. Оценить вероятность того, что из обследованных 10 000 жителей 4 окажутся заболевшими. 18. Если при транспортировке ампул с некоторым препаратом со склада в аптеку в среднем повреждается 0,1% ампул, то какова вероятность повреждения двух ампул при транспортировке 3000 ампул? 19. Имеется двадцать коробок с яблоками, причем количество яблок в них составляет 10, 9, 11, 10, 12, 8, 11, 9, 10, 10, 11, 8, 9, 10, 9, 11, 12, 10, 9 и 11 штук. Составить закон распределения случайной величины X, определяемой как количество яблок в произвольно выбранной коробке, и найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой величины. 20. Число фармацевтов в каждой из 15 аптек некоторого района составляет соответственно 4, 7, 5, 6, 4, 5, 3, 6, 4, 5, 5, 4, 6, 5 и 6 человек. Составить закон распределения случайной величины X, определяемой как число фармацевтов в произвольно выбранной аптеке (из этих 15 аптек), найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой величины. 21. Найти вероятность того, что значение непрерывной нормально распределенной величины окажется в интервале 22. Предполагая, что рН крови человека подчиняется нормальному закону распределения с математическим ожиданием 23. Предполагая закон распределения роста студентов нормальным с математическим ожиданием Задание Проанализировать массив R-R –интервалов, применяя статистический, графический и вероятностный подход. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , где
, где  — математическое ожидание, а
— математическое ожидание, а  — среднее квадратическое отклонение этой величины.
— среднее квадратическое отклонение этой величины. и средним квадратическим отклонением
и средним квадратическим отклонением  , найти вероятность того, что у произвольно выбранного человека уровень рН находится между 7,3 и 7,5.
, найти вероятность того, что у произвольно выбранного человека уровень рН находится между 7,3 и 7,5. см и дисперсией
см и дисперсией 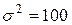 см2 , найти вероятность того, что рост произвольно выбранного студента окажется в пределах от 180 до 190 см.
см2 , найти вероятность того, что рост произвольно выбранного студента окажется в пределах от 180 до 190 см.