Факторный анализ интеллекта

Психологические исследования, цель которых — идентификация психических черт, выросли из интереса ученых к природе и структуре человеческого интеллекта.¹ Такие исследования начинаются с вычисления интеркорреляций показателей, полученных на выборке испытуемых по широкому набору тестов способностей. Затем корреляционная матрица подвергается дальнейшему математическому анализу с целью выявления общих факторов или черт на множестве тестов. Имеющиеся для достижения этой цели разнообразные методы объединены под общим названием факторного анализа.

Факторная матрица.Основная цель факторного анализа (ФА) — упростить описание данных посредством сокращения числа необходимых переменных или, иначе говоря, сократить размерность пространства описания данных. Так, если установлено, что пяти факторов достаточно для объяснения всей общей дисперсии в батарее из 20 тестов, то в большинстве случаев исходные 20 показателей без существенной потери информации можно заменить пятью новыми показателями. На практике обычно из совокупности исходных тестов сохраняют те, которые дают лучшие меры каждого из факторов.

Факторный анализ, независимо от используемых методов, начинается с обработки таблицы интеркорреляций, полученных на множестве тестов, известной как корреляционная матрица, а заканчивается получением факторной матрицы, т. е. таблицы, показывающей вес или нагрузку каждого из факторов по каждому тесту. Табл. 11-1 Представляет собой гипотетическую факторную матрицу, включающую всего два фак-

История этого вопроса затрагивается в Anastasi (1984b).

Часть 3. Тестирование способностей

Таблица ll-i Гипотетическая факторная матрица I

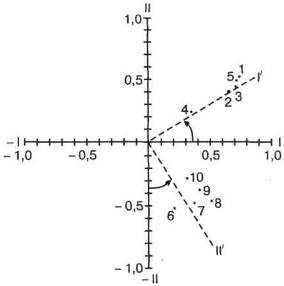
тора. Факторы перечисляются в верхней строке таблицы от более значимого к менее значимому, а их веса в каждом из 10 тестов даны в соответствующих столбцах.

Разработано несколько различных методов разложения множества переменных на общие факторы. Еще в начале века Карл Пирсон (Pearson, 1901) показал способ решения задачи такого типа, а Чарльз Спирмен (С. Spearman, 1904,1927) заложил основы современного факторного анализа. Т. Келли (Т. L. Kelly, 1935) и Л. Тёрстоун (L. L. Thur-stone, 1947) в Америке и С. Берт (С. Burt, 1941) в Англии много сделали для усовершенствования этого метода. Альтернативные методы, модификации и усовершенствования ФА разрабатывались многими авторами. Наличие быстродействующих вычислительных машин ведет к принятию более тонких и, соответственно, трудоемких методов ФА. Несмотря на разницу в исходных постулатах, большинство этих методов дает сходные результаты. Для детального знакомства с методами ФА читатель может обратиться к учебникам Comrey, & Lee (1992) или Loehlin (1992). Краткий и простой обзор основных понятий и методов ФА можно найти в книгах Kim, & Mueller (1978a, 1978 b) и P. Kline (1993).

Рассмотрение математических основ или вычислительных процедур ФА не входит в задачи этой книги. К счастью, для понимания результатов ФА не обязательно владеть его специальной методологией. Даже без знания того, как были вычислены факторные нагрузки, можно понять, каким образом следует использовать факторную матрицу для идентификации и интерпретации факторов. Тем не менее, чтобы с пользой читать публикации, посвященные факторно-аналитическим исследованиям, знакомство с некоторыми понятиями и терминами ФА не помешает.

Оси координат. Принято представлять факторы геометрически в виде осей координат, относительно которых каждый тест может быть изображен в виде точки. Рис-11-1 поясняет эту процедуру. На этом графике каждый из 10 тестов, приведенных в табл. 11-1, отображен в виде точки относительно двух факторов, которые соответствуют осям I и И. Так, тест 1 представлен точкой с координатами 0,74 по оси I и 0,54 по оси II. Точки, представляющие остальные 9 тестов, построены аналогичным способом, с использованием значений весов из табл. 10-1. Все эеса по фактору I положи-

Глава 11. Природа интеллекта

Рис. 11-1. Гипотетическое факторное отображение, показывающее веса двух групповых факторов по каждому из 10 тестов

тельны, веса по фактору II как положительны, так и отрицательны, что также отражено на рис. 11-1, где тесты с 1-го по 5-го образуют кластер в одной части координатной плоскости, а тесты с 6-го по 10-го — в другой.

В этой связи следует заметить, что положение осей координат не фиксировано данными. Исходная таблица корреляций определяет лишь положение тестов (т. е. точек на рис. 11-1) относительно друг друга. Те же точки можно нанести на плоскость с любым положением координатных осей. По этой причине при проведении факторного анализа обычно вращают оси до тех пор, пока не получают наиболее приемлемого и легко интерпретируемого отображения. Эта процедура вполне обоснованна и в чем-то похожа на измерение долготы, скажем, не от гринвичского меридиана, а от проходящего через Чикаго.

На рис. 11-1 полученные после вращения оси I' и II' показаны пунктирными линиями¹. Это вращение выполнено в соответствии с предложенными Тёрстоуном критериями положительного многообразия и простой структуры. Первый предполагает вращение осей до положения, при котором исключаются все значимые отрицательные веса. Большинство психологов считают отрицательные факторные нагрузки логически несоответствующими тестам способностей, так как такая нагрузка означает, что чем выше оценка индивидуума по специфическому фактору, тем ниже будет его результат по соответствующему тесту. Критерий простой структуры, в сущности, означает, что каждый тест должен иметь нагрузки по как можно меньшему числу факто-

Читатель, вероятно, заметил, что полученную в результате вращения ось II следовало бы обозначить как -II, чтобы привести в соответствие с неповернутой осью -II. Однако какой из полюсов оси выбрать в качестве положительного или отрицательного, дело произвольное. В нашем примере полученная вращением ось II была «перевернута», с тем чтобы избавиться от отрицательных весов.

Часть 3. Тестирование способностей

Таблица Ц_2 Факторная матрица после вращения

(По данным, представленным на рис. 11-1)

ров.¹ Выполнение обоих критериев дает факторы, которые можно наиболее легко и однозначно интерпретировать. Если тест имеет высокую нагрузку по одному фактору и не имеет значимых нагрузок по другим факторам, мы можем кое-что узнать о природе этого фактора, изучив содержание данного теста. Напротив, если тест имеет средние или низкие нагрузки по шести факторам, то он мало что скажет нам о природе любого из них.

На рис. 11-1 хорошо видно, что после вращения осей координат все вербальные тесты (1-5) располагаются вдоль или очень близко к оси Г, а числовые тесты (6-10) тесно группируются вокруг оси II'. Новые факторные нагрузки, измеренные относительно повернутых осей, приведены в табл. 11-2. Читатель может легко проверить значения этих факторных нагрузок, изготовив из бумаги «масштабную линейку» со шкалой единиц, соответствующей масштабу координатных осей. С помощью этой линейки можно измерить длину отрезков, соответствующих проекциям точек (тестов) на повернутые оси координат. Факторные нагрузки в табл. 11-2 не имеют отрицательных значений, за исключением пренебрежимо малых величин, явно относимых к ошибкам выборки. Все вербальные тесты имеют высокие нагрузки по фактору I и практически нулевые — по фактору II'. Числовые тесты, напротив, имеют высокие нагрузки по фактору If и пренебрежимо низкие — по фактору Г. Таким образом, вращение координатных осей существенно упростило идентификацию и называние обоих факторов, а также описание факторного состава каждого теста. На практике число факторов часто оказывается больше двух, что, разумеется, усложняет их геометрическое представление и статистический анализ, но не изменяет существа рассмотренной процедуры.

Некоторые исследователи руководствуются теоретической моделью как принципом вращения осей. Кроме того, принимается в расчет неизменность, или подтверж-

¹ Этот критерий требует, чтобы по некоторым факторам тесты имели нагрузки, значимо не отличающиеся от нуля. Такое требование можно теперь проверить эмпирически, используя доступные статистические процедуры для нахождения стандартной ошибки факторных нагрузок (Cudeck, & O'Delb 1994).

Глава 11. Природа интеллекта 337

дение одних и тех же факторов в независимо выполненных, но сравнимых исследованиях. В настоящее время факторный анализ все чаще используется в роли подтверждающего, чем исследовательского метода. Нередко его сочетают с моделированием структурными уравнениями (см. главу 5) для оценивания теоретически сформулированной модели вклада различных переменных в выполнение задачи (см., например, Loehlin, 1992).

Интерпретация факторов.Получив после процедуры вращения факторное решение (или, проще говоря, факторную матрицу), мы можем переходить к интерпретации и наименованию факторов. Этот этап работы скорее требует психологической интуиции, нежели статистической подготовки. Чтобы понять природу конкретного фактора, нам ничего не остается, как изучить тесты, имеющие высокие нагрузки по этому фактору, и попытаться обнаружить общие для них психологические процессы. Чем больше оказывается тестов с высокими нагрузками по данному фактору, тем легче раскрыть его природу. Из табл. 11-2, к примеру, сразу видно, что фактор Г вербальный, а фактор II' числовой.

Приведенные в табл. 11-2 факторные нагрузки отображают к тому же корреляцию каждого теста с фактором.¹ Напомним, что эта корреляция есть не что иное, как факторная валидность теста (глава 5). По табл. 11-2 можно, к примеру, определить, что факторная валидность словарного теста как средства измерения вербального фактора равна 0,91. Факторная валидность теста на сложение относительно числового фактора равна 0,55. Очевидно, что первые 5 тестов имеют пренебрежимо малую валидность как средства измерения числового фактора, а последние 5 — практически нулевую валидность в качестве мер вербального фактора.

Факторная композиция теста.Одна из основных теорем ФА гласит: полная дисперсия теста равна сумме дисперсий, обусловленных действием общих (разделяемых с другими тестами) и специфических (встречающихся только в одном таком тесте) факторов, плюс дисперсия ошибок.

Мы уже сталкивались с дисперсией ошибок при анализе показателей тестов (глава 4). Если, к примеру, коэффициент надежности теста равен 0,83, то это значит, что 17 % дисперсии показателей по этому тесту составляет дисперсия ошибок (1,00 - 0,83 = 0,17). При помощи факторного анализа можно провести более тонкий анализ источников дисперсии, влияющих на выполнение того или иного теста.

Рассмотрим два гипотетических теста, информация о которых представлена в табл. 11 -3. В ней для каждого теста указаны его факторные нагрузки по Вербальному (V), Числовому (N) и Логическому (R) факторам, а также коэффициенты надежности этих тестов. Так как факторная нагрузка представляет собой еще и корреляцию между тестом и фактором, квадрат факторной нагрузки указывает нам долю общей Дисперсии между тестом и соответствующим фактором. Приведенные в правой части табл. 11-3 квадраты факторных нагрузок показывают пропорциональный вклад каждого фактора в полную дисперсию показателей теста. Так, в тесте на арифметическое Рассуждение 16 % дисперсии можно приписать вербальному, 30 % — числовому и 36 % —

Это справедливо только для случаев, когда применяется ортогональное вращение. При облическом (косоугольном) вращении, речь о котором пойдет в этом разделе позднее, факторные нагрузки и факторные корреляции связаны между собой простым отношением, позволяющим с помощью соответствующих вычислений легко получить одно из другого.

Часть 3. Тестирование способностей

Таблица Ц~з

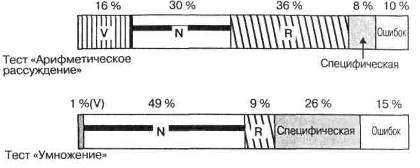
логическому факторам. Дисперсия ошибок в последнем столбце определена простым вычитанием коэффициента надежности из полной дисперсии (1,00 - 0,90 = 0,10). Цифры слева, указанные рядом с дисперсиями ошибок, отражают специфичность каждого теста, т. е. долю его «истинной» дисперсии, не разделяемую ни с одним другим тестом, вместе с которыми данный тест подвергался факторному анализу. Для теста на арифметическое рассуждение мы получаем следующие величины:

0,16 + 0,30 + 0,36 + 0,10 - 0,92 1,00-0,92 = 0,08

На рис. 11-2 структура полной дисперсии для двух тестов (в соответствии с данными табл. 11-3) представлена в графической форме.

Любой индивидуальный результат по этим двум тестам определяется величиной соответствующих способностей, или факторов, которыми обладает конкретный человек, а также относительными весами этих факторов в конкретном тесте. Поэтому если бы мы располагали чьими-то показателями по вербальному, числовому и логическому факторам, выраженными в одинаковых единицах измерения, то могли бы взвесить каждый показатель, умножая его на соответствующую факторную нагрузку. Сумма этих произведений дала бы нам оценку показателя данного человека по данному тесту. Чем меньше вклад специфического и случайного факторов в этот тест, тем точней будет наша оценка.

Согласно гипотетическим данным табл. 11-3, если конкретный человек имеет очень высокую оценку по Вербальному фактору (V), это гораздо больше поможет ему при выполнении теста на арифметическое рассуждение, чем теста на умножение. Фактически, содействие фактора Показалось бы в 4 раза сильнее в тесте на арифметическое рассуждение по сравнению с тестом на умножение, поскольку вес этого фактора в 4 раза больше в первом тесте, чем во втором (0,40 против 0,10). Из трех общих факторов Числовой фактор (Л⁷) имел бы наибольшее влияние в тесте на умножение (нагрузка = 0,70), а Логический фактор (/?) — в тесте на арифметическое рассуждение (нагрузка - 0,60).

Факторные нагрузки и корреляция.Вторая основная теорема ФА касается соотношения факторных нагрузок и корреляций между переменными. Корреляция меЖДУ любыми двумя переменными равняется сумме парных произведений их нагрузок по

Глава 11. Природа интеллекта

Рис. 11-2.Процентное соотношение общей дисперсии, специфической дисперсии и дисперсии ошибок в двух гипотетических тестах

(По данным табл. 11-3)

общим факторам. Так как специфический фактор и фактор ошибки каждой переменной уникальны, они не вносят никакого вклада в корреляцию между переменными. Корреляция между любыми двумя переменными зависит только от тех факторов, которые являются общими для этих двух переменных. Чем больше веса таких общих факторов в обеих переменных, тем выше будет между ними корреляция. Корреляцию между двумя тестами из табл. 11-3 можно найти перемножением нагрузок каждого из трех общих факторов по этим двум тестам и сложением полученных произведений:

r12= (0,40)(0,10)+ (0,55)(0,70)+ (0,60)(0,30)= 0,60.

Косоугольная система координат и факторы второго порядка.Изображенные на рис. 11-1 оси называются ортогональными, так как они строго перпендикулярны друг другу. Иногда кластеры тестов располагаются таким образом, что лучшего соответствия используемым критериям удается достичь при использовании облических, или косоугольных, осей. В таком случае уже сами факторы коррелируют друг с другом. Одни исследователи утверждали, что использование ортогональных, или некоррели-рующих, факторов всегда предпочтительнее, поскольку такие факторы дают более простую и четкую картину взаимосвязи черт. Другие настаивают на том, что косоугольную систему координат следует использовать всякий раз, когда она лучше соответствует изучаемым данным, поскольку большинство имеющих ясный физический смысл категорий и не должны быть независимыми. Очевидный пример — рост и вес. Хотя хорошо известно, что рост и вес высоко коррелируют между собой, они оказались весьма полезными категориями при оценке телосложения.

Когда факторы коррелируют между собой, существующие между ними интеркорреляции можно подвергнуть тому же статистическому анализу, который мы применяем к интеркорреляциям между тестами. Иными словами, у нас есть возможность «фак-торизовать факторы» и получить факторы второго порядка. Этот способ обработки Данных был использован в ряде исследований таких переменных, как способности и черты личности. В некоторых исследованиях с использованием тестов способностей был получен единственный общий фактор второго порядка. Как правило, американские исследователи, применяющие факторный анализ, начинают с объяснения как можно большей части общей дисперсии групповыми факторами и только затем выявляют

Часть 3- Тестирование способностей

общий фактор как фактор второго порядка, если данные подтверждают его наличие. У английских психологов, напротив, принято начинать с общего фактора, которому приписывается основная доля общей дисперсии, а затем возвращаться к групповым факторам для объяснения остаточной корреляции. Эта разница в методиках есть следствие теоретических различий, о которых речь пойдет в следующем разделе.

Теории организации черт

На протяжении более полувека предпринимались многочисленные попытки с помощью статистических методов ФА понять природу и организацию способностей, связанных с разнообразной человеческой деятельностью. Тем не менее эти методы до сих пор остаются наиболее тесно связанными с изучением когнитивных способностей, или «интеллекта», — направлением, в рамках которого и зародился факторный анализ. Недавно составленный обзор всех опубликованных факторно-аналитических исследований когнитивных способностей дает впечатляющую сводку состояния дел в этой области (Carroll, 1993). Охватывая 70-летний период исследований, работа Кэрролла представляет собой гораздо больше, чем литературный обзор, ибо содержит еще и повторный анализ 450 наборов данных из оригинальных исследований. К тому же в ней описаны различные теоретические модели интеллекта и дана их оценка в исторической перспективе. В этом разделе мы рассмотрим лишь некоторые широко известные теории интеллекта, выбор которых обусловлен их воздействием на конструирование и использование тестов.

Двухфакторная теория.Первой теорией организации черт, основанной на статистическом анализе показателей тестов, была двухфакторная теория, развитая английским психологом Чарльзом Спирменом (Spearman, 1904; 1927). В своем первоначальном виде эта теория утверждала, что все виды интеллектуальной активности используют долю единого общего фактора, названного генеральным, или фактором g (от англ. general). Кроме того, в теории Спирмена постулировалось наличие многочисленных специфических, или s-факторов (от англ. specific), каждый из которых сказывается на выполнении только одной из интеллектуальных функций. Положительная корреляция между любыми двумя функциями приписывалась, таким образом, действию фактора g. Чем больше эти две функции были «насыщены» {saturated) фактором g, тем выше должна бы быть корреляция между ними. Напротив, присутствие специфических факторов вело к снижению корреляции между функциями.

Несмотря на постулирование Спирменом двух типов факторов — генерального и специфических, фактор g рассматривается в его теории как единственная причина корреляции. Поэтому, в отличие от других теорий связи черт, эту теорию было бы точнее называть однофакторной, однако она сохранила свое первоначальное название. Рис. 11-3 иллюстрирует основополагающий принцип корреляций тестов согласно этой теории. Из этой схемы видно, что, в соответствии с теорией Спирмена, тесты 1 и I должны высоко коррелировать между собой, поскольку каждый сильно насыщен фактором g, о чем свидетельствуют заштрихованные участки. Незаштрихованным частям каждого теста соответствуют специфический фактор и дисперсия ошибок. Тест 3 Д^оЛ" жен слабо коррелировать с каждым из двух других тестов, поскольку включает очень малую долю фактора g.

Глава 11. Природа интеллекта

Рис. 11-3. Принципиальная модель корреляции в двухфакторной теории

Согласно двухфакторной теории, целью психологического тестирования должно быть измерение величины фактора g у каждого индивидуума. Если этот фактор пронизывает все способности, тогда он дает нам единственную основу для предсказания результатов деятельности индивидуума в разных ситуациях. Специфические факторы измерять бесполезно, так как каждый из них, по определению, сказывается только на какой-то одной функции. Вот почему Ч. Спирмен предложил заменить разнородную совокупность заданий, встречаемых в тестах интеллекта, единственным, пусть односторонним, тестом, но при этом высоко насыщенным фактором g. Он полагал, что тесты на абстрактные отношения, по всей вероятности, лучше всех других измеряют g и потому могут быть использованы для этой цели. Примерами тестов, разработанных для измерения g, являются Прогрессивные матрицы Равена и Культурно-свободный тест интеллекта Кэттелла (Cattell's Culture Fair Intelligence Test).

С самого начала Спирмен понимал, что двухфакторная теория нуждается в уточнении. Когда сравниваемые деятельности достаточно похожи, корреляция между ними может достигать величины, превышающей степень связи между переменными, объяснимую действием фактора g. Поэтому в добавление к генеральному и специфическим факторам, вероятно, существует промежуточный класс факторов, не столь универсальных, как g, но и не столь специфичных, как s-факторы. Такой фактор, общий только для группы (а не для всех вообще) интеллектуальных функций, был назван групповым фактором. В первых вариантах своей теории Спирмен допускал возможность весьма узких и пренебрежимо малых групповых факторов. Позднее, под давлением фактов, полученных в исследованиях некоторых его учеников, он стал использовать в своих теоретических построениях гораздо более широкие групповые факторы, такие как арифметические, технические и лингвистические способности.

Многофакторные теории.Преобладавший в американской психологии взгляд на организацию черт, основанный на ранних факторно-аналитических исследованиях, заключался в признании ряда довольно широких групповых факторов, каждый из которых мог входить с разными весами в различные тесты. Например, вербальный фактор мог бы иметь значительный вес в словарном тесте, несколько меньший вес — в Тесте словесных аналогий, и еще меньший — в тесте на арифметическое рассуждение. На рис. 11-4 в наглядной форме представлены интеркорреляции пяти тестов с точки

Часть 3. Тестирование способностей

зрения многофакторной модели. Корреляции тестов 1, 2 и 3 друг с другом — следствие их общих нагрузок вербальным фактором ( V), Аналогично этому, корреляция между тестами 3 и 5 — результат действия пространственного фактора (5), а между тестами 4 и 5 — числового (N). Тесты 3 и 5 отличаются сложной факторной композицией: каждый имеет существенные нагрузки более чем по одному фактору (тест 3 — по факторам Уи 5, а тест 5 — по факторам SnN). Обращаясь к рассмотренной в предыдущем разделе второй основной теореме ФА, мы можем сделать некоторые выводы об относительной величине этих интеркорреляций. Например, тест 3 будет сильнее коррелировать с тестом 5, чем с тестом 2, потому что веса фактора S в тестах 3 и 5 (области с диагональной штриховкой) больше, чем веса фактора V в тестах 2 и 3 (области с горизонтальной штриховкой).

Публикация программной книги Т. Келли Crossroads in the Mind of Man (T. L. Kelly, 1928) подготовила почву для большого числа исследований, нацеленных на выявление групповых факторов. Важнейшими среди предложенного Келли набора факторов были следующие: манипулирование пространственными отношениями, легкость оперирования числами, легкость оперирования словесным материалом, а также память и скорость. Этот перечень был позднее переработан и дополнен исследователями, использовавшими более современные методы ФА, рассмотренные в предыдущем разделе.

Одним из ведущих представителей многофакторной теории был Л. Л. Тёрстоун. Основываясь на обширных исследованиях, как своих собственных, так и учеников, Тёрстоун выделил около дюжины групповых факторов, которые он назвал «первичными умственными способностями». К факторам, чаще всего подтверждавшимся в работах самого Тёрстоуна и других независимых исследователей (French, 1951; Наг-man, 1975; Thurstone, 1938; Thurstone, & Thurstone, 1941), относятся следующие:

V. Вербальное понимание (Verbal Comprehension). Главный фактор в таких тестах, как понимание прочитанного, словесные аналогии, восстановление порядка слов в предложениях, вербальное рассуждение и подбор пословиц. Данный фактор наиболее адекватно измеряется словарными тестами.

Рис. 11-4. Принципиальная модель корреляции в многофакторных теориях

Глава 11. Природа интеллекта 343

W. Беглость речи (Word Fluency). Выявляется в таких тестах, как анаграммы, подбор рифм или называние слов данной категории (например, мужские имена или слова, начинающиеся с буквы Т).

N. Числовой (Number). Почти полностью отождествляется со скоростью и точностью простых арифметических вычислений.

S. Пространственный (Space). Может представлять собой два разных фактора. Один связан с восприятием фиксированных пространственных или геометрических отношений, другой с манипулированием зрительными образами, при котором изменение положения или трансформацию объекта необходимо представить зрительно (McGee, 1979; Portegal, 1982).

М. Ассоциативная память (Associative Memory). В основном обнаруживается в тестах, требующих механической памяти на ассоциативные пары. Есть некоторые основания предполагать, что этот фактор может отражать степень использования опор памяти (Christal, 1958), а противоречит существованию более широкого фактора, присутствующего во всех тестах памяти. Некоторые исследования подтверждают наличие ограниченных факторов памяти, таких как память на временные последовательности и положение в пространстве.

Р. Перцептивная скорость (Perceptual Speed). Быстрое и точное зрительное восприятие деталей, сходства и различий. Возможно, это тот же фактор, что и фактор скорости, выявленный Т. Л. Келли и другими предшественниками, по крайней мере, он относится к ряду факторов, идентифицированных позднее в задачах на восприятие (Thurstone, 1944).

/ (или R). Индукция (или Общий вывод) — (Induction, or General Reasoning). Этот фактор установлен наименее четко. Тёрстоун первоначально предположил наличие индуктивного и дедуктивного факторов. Последний лучше всего измерялся тестами на силлогистический вывод, а первый — тестами, требующими от испытуемого найти принцип (правило, закономерность и т. п.), как в тестах на завершение числовых последовательностей. Доказательства наличия дедуктивного фактора оказались, однако, гораздо слабее доказательств в пользу существования индуктивного фактора. Кроме того, некоторые исследователи исходили из предположения, что фактор логического мышления лучше всего измеряется тестами на арифметическое мышление.

Следует отметить, что различия между общими, групповыми и специфическими факторами не столь существенны, как может показаться в первый момент. Если число или разнообразие тестов в батарее невелико, одним общим фактором можно объяснить все корреляции между ними. Но когда те же самые тесты включены в батарею с более разнородным составом тестов, исходный общий фактор может выделиться как групповой, т. е. общий только для некоторых, но не для всех тестов. Аналогично этому, некоторый фактор может быть представлен только одним тестом в исходной батарее, но разделяться несколькими тестами в более крупной батарее. Такой фактор был бы идентифицирован как специфический в первой батарее, но оказался бы групповым в более полной, комплексной батарее. Поэтому вряд ли нужно удивляться, что интенсивные факторные исследования специальных областей выявили множество факторов вместо одной или двух первичных умственных способностей, первоначально идентифицированных в каждой такой области. Именно это и произошло в исследованиях вербальных и перцептивных тестов, тестов памяти и тестов на логическое рассуждение.

Складывается представление, что факторные исследования привели к ошеломительному «размножению» факторов. Число когнитивных факторов, описанных на се-

Часть 3- Тестирование способностей

годняшний день различными исследователями, перевалило за 100. Относительного порядка в этой сфере удалось достичь путем перекрестной идентификации факторов описанных разными исследователями и зачастую под разными названиями (Ekstrom' French, & Harman, 1979; French, 1951; Harman, 1975). Такую перекрестную идентификацию можно выполнить только в тех случаях, когда в сравниваемых исследованиях используется ряд общих тестов. Чтобы облегчить этот процесс, группой сторонников применения факторного анализа был составлен комплект «базовых тестов» (reference tests), измеряющих установленные к настоящему времени главные факторы способностей. Этот комплект, распространяемый Службой тестирования в образовании (Ekstrom, French, Harman, & Dermen, 1976; ETS kit, 1976), облегчает разным исследователям планировать факторные исследования с включением ряда общих тестов в используемые ими батареи.

Очевидно, что даже после всех этих попыток упростить ситуацию и согласовать действия исследователей в области изучения способностей методами ФА, число факторов остается большим. Человеческое поведение изменчиво и сложно, и, по-видимому, наивно ожидать, что его можно адекватно описать с помощью дюжины или около того факторов. Но для конкретных целей можно подобрать подходящие факторы в отношении как их природы, так и их широты. Так, если бы мы отбирали кандидатов для трудной и высокоспециализированной работы технического характера, то, вероятно, захотели бы измерить у них довольно узкие факторы восприятия и пространственных отношений, наиболее отвечающие требованиям будущей работы. С другой стороны, при отборе студентов колледжа, мы бы отдали явное предпочтение нескольким широким факторам, таким как вербальное понимание, легкость оперирования числами и умение делать общие выводы.

Модель структуры интеллекта.Некоторые исследователи, работающие с факторным анализом, пытались упростить картину взаимосвязей черт путем придания им некой упорядоченной структуры. Основываясь на своих более чем 20-летних факторно-аналитических исследованиях, Дж. Гилфорд (Guilford, 1967,1988; Guilford, & Но-epfner, 1971) предложил кубическую модель, которую назвал моделью «структуры интеллекта» (structure-oj"-intellectmodel'или, сокращенно, SI model). Изображенная на рис. 11-5 модель¹ классифицирует черты интеллекта (intellectual traits) по трем измерениям.

Операции — то, что делает респондент. К ним относятся восприятие (cognition), запоминание и сохранение информации, дивергентное (проявляющееся в творческой активности) продуцирование, конвергентное продуцирование и оценка.

Содержание — характер материалов или информации, с которыми выполняются операции. Сфера содержания делится на зрительную, слуховую, символическую (например, буквы, цифры), семантическую (например, слова) и поведенческую (информация о других людях, их поведении, аттитюдах, потребностях и т. д.) области.

Продукты — форма, в которой информация обрабатывается респондентом. Продукты подразделяются на элементы, классы, отношения, системы, преобразования и импликации.

¹ В результате последующих исследований Гилфорда его модель претерпела изменения и отличается от более ранней (Guilford, 1967) разделением такого аспекта содержания, как образная (Jigu^ral' информация, на зрительную и слуховую составляющие, а также разделением такого аспекта опер³' ций, как память, на запоминание и сохранение материала (Guilford, 1988).

Глава 11. Природа интеллекта

Рис. 11-5.Трехмерная модель структуры интеллекта (Из Guilford, 1988, р. 3. Copyright © 1988 by Educational and Psychological Measurement.

Воспроизведено с разрешения)

Поскольку такая классификация содержит 6x5x6 категорий, в этой модели получается 180 ячеек. Предполагается, что каждой ячейке соответствует по меньшей мере один фактор, или способность, а некоторые ячейки могут содержать более одного фактора. Каждый фактор описывается в трех измерениях. К моменту завершения 20 -летнего Проекта исследования способностей {Aptitude Research Project) — скоординированной программы исследований Sl-model — Дж. Гилфорд и его коллеги идентифицировали 98 из предсказанных на основе этой модели факторов (Guilford, & Hoepfner, 1971). Алфавитный перечень и краткое описание множества тестов, разработанных в рамках этого 20-летнего проекта, можно найти в книге Дж. Гилфорда и Р. Хопфнера (Guilford, & Hoepfner, 1971, Appendix В).

Хотя один тест все же был разработан непосредственно на основе Sl-model, а именно — СИ-тест способностей к обучению {Structure of Intellect Learning Abilities Test — Meeker, Meeker, & Roid, 1985) , сама эта модель практически не повлияла на разработку и применение тестов общего пользования.¹ Следует, однако, учитывать то обстоятельство, что Sl-model, как и все другие модели организации черт, дает всего одну

Подробнее об этом см. Carroll (1993), особенно р. 57-60.

Часть 3. Тестирование способностей

схему отображения полученных корреляций между переменными. Вследствие метода, используемого при вращении осей, эмпирическое подтверждение Sl-model не служит основанием для опровержения других моделей (Carroll, 1972; Horn & Knapp 1973). Вполне вероятно, что различные вращения одних и тех же данных могут обнаружить одинаково тесное их соответствие другим моделям. Повторный анализ исходных факторно-аналитических данных Гилфорда действительно показал, что они лучше соответствовали другим моделям, чем его оригинальной Sl-model, и при этом получали менее противоречивое теоретическое и практическое истолкование (Bachelor, 1989; Carroll, 1993).

Не нашли, что искали? Воспользуйтесь поиском по сайту: