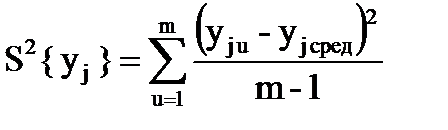|
|
Задача 2. Статистический анализ двумерной последовательности случайных величинЦель работы. Освоить компетенции выполнения статистического анализа двумерных данных, выявить зависимость (связь) между случайными величинами. Взаимосвязь может быть оценена следующими методами: 1) Визуальный метод 2) Корреляционный анализ 3) Регрессионный анализ
Исходные данные
В качестве исходных данных принято двух последовательных случайных величин: первая - _______________________________________________; вторая - ______________________________________________ Исходные данные представлены в таблице 1.
Таблица 1 – Исходные данные
Примем: в качестве аргумента Xi - __________________________; в качестве функции Yi-__________________________.
Визуальный анализ
Определение метода анализа
По данным таблицы 1 построен точечный график (рис. 1).
Рисунок 1 – Точечный график
Корреляционный анализ
Корреляционная зависимость – (определение) . Корреляционный анализ выполнен с помощью пакета «Анализ данных» программы Excel, результаты которого показаны в таблице 2.
Таблица 2 - результаты корреляционного анализа
Вывод: _________________________________________________
Регрессионный анализ
Регрессионный анализ – (определение). Регрессионный анализ заданных последовательностей выполнен с помощью режима Регрессия пакета «Анализ данных» программы MS Excel. Сгенерируются результаты по регрессионной статистике, представленные в таблице 3.
Таблица 3- Результаты регрессионного анализа
Расчитанные в таблицах характеристики представляют собой: Дать описание приведенных в таблицах характеристик.
Регрессионные модели
Построение регрессионных моделей выполнено с помощью команды «Построение линии тренда» программы Excel. На нижеприведенных рисунках показаны различные регрессионные модели, описывающие связь между двумя заданными последовательностями случайных величин.
Рисунок 2 – Экспоненциальная модель
Рисунок 3 – Линейная модель
Рисунок 4 – Логарифмическая модель
Рисунок 5 – Полиномиальная модель
Рисунок 6 – Полиномиальная модель
В таблице 3 показаны сводные данные по всем построенным моделям.
Вывод: _______________________________________________
Заключение
________________________________________________________
Часть 2 ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТОВ
1. Реалистичное содержание целевой функции В качестве целевой функции (функции отклика, зависимой переменной, реакции системы на воздействие факторов Xi) Y принята _______________:
Y = f(Х1, Х2, Х3).
2. Реалистичное содержание (сущность) факторов
В качестве факторов функции отклика Xi принимаются:
X1 - _______________________________; X2 - _______________________________; Х3 - _______________________________.
Уровни варьирования значений факторов
Минимальные и максимальные значения факторов приняты следующие:
Среднее значение фактора Среднее значение фактора определяется по формуле:
X10 = ______________________; X20 = ______________________; X30 = ______________________.
Интервалы варьирования фактора Интервал варьирования определяется по формуле:
dx1 = X10 – X1min = _________________________. dx2 = X20 – X2min = __________________________. dx3 = X30 – X3min = __________________________.
Корректность определения значений факторов
Нормированные значения факторов Нормированные значения определяются формулой:
Хн1 = _____________________; Хн2 = _____________________; Хн3= _____________________.
8. Матрица планирования полного факторного эксперимента Полный двухфакторного эксперимента первый столбец вводится искусственным путем и постоянен и равен 1.
Экспериментальные значения целевой функции
Дисперсия среднего арифметического для каждой строки матрицы эксперимента (каждого опыта) Дисперсия среднего арифметического определяется формулой:
где m – количество параллельных опытов в строке матриц.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

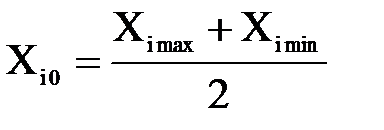 .
.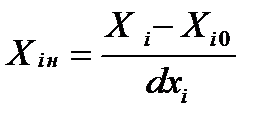 .
.