ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ ПРОЦЕССА ИСТЕЧЕНИЯ ГАЗА ЧЕРЕЗ СОПЛОВЫЕ КАНАЛЫ 3 глава

Рис. 3.1. Изменение удельного объема v, скорости c (α – скорости звука) и площади сечения соплового канала f при изменении давления газа в нем от р = р_о до р = 0

При ε > ε_КР и р_К > р_КР истечение докритическое, сопло должно быть суживающимся.

При ε < ε_КР и р_К < р_КР истечение сверхкритическое, сопло должно быть комбинированным с расширяющейся частью (сопло Лаваля).

При ε < ε_КР и р_К < р_Р истечение через суживающееся сопло будет критическим, в выходном сечении сопла давление будет критическим, а расширение газа от р_КР до р_К будет происходить за пределами соплового канала.

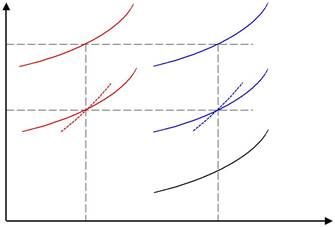
В режиме критического истечения через суживающееся сопло при всех значениях р_К < р_КР давление и скорость в выходном сечении сопла будут критическими и неизменными, соответст-венно и расход газа через сопло будет постоянным, соответст-вующим максимальной пропускной способности данного сопла при заданных р_о и Т_о (уравнения (8) и (9), рис. 3.2).

G

Gmax2

Gmax1

0 eкр1 eкр2 e₁=1 e2=1 ^e

Рис. 3.2. Расходные характеристики сопла при различных критических перепадах давлений и одинаковых начальных температурах

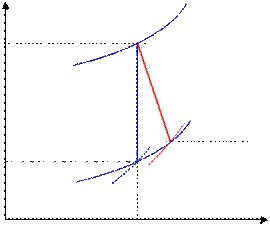
Увеличить пропускную способность данного сопла возможно только увеличением давления на входе в него. В этом случае происходит увеличение критического давления, что приводит к снижению объема в выходном сечении сопла, а критическая скорость остается неизменной, поскольку она зависит только от начальной температуры (рис. 3.3).

s

Рис. 3.3. Процессы критического расширения газа в сопловых каналах при одинаковых Т_о и р_о2> р_о1

Необратимый (действительный) процесс истечения газа че-рез сопло характеризуется наличием трения, что приводит к смещению адиабаты процесса в сторону увеличения энтропии

(рис. 3.4).

Необратимость процесса истечения приводит к увеличению удельного объема, энтальпии и температуры газа в данном се-чении сопла по сравнению с аналогичными параметрами газа в данном сечении сопла при обратимом истечении. В свою оче-редь, увеличение этих параметров газа приводит к снижению скорости и расхода газа в действительном процессе истечения по сравнению с идеальным истечением газа.

Снижение скорости газа в действительном процессе истече-ния характеризует скоростной коэффициент сопла φ:

T1i

V₁

s

Рис. 3.4. Необратимый процесс расширения газа в сопловом канале 1-2’ в Т,s-диаграмме

Потери располагаемой работы из-за наличия трения в реаль-ном процессе истечения характеризует коэффициент потерь сопла x или адиабатный коэффициент сопла h_с:

В выражениях (11) и (12) использование температур приме-нимо только к газам с постоянными изобарными теплоемкостя-ми.

Коэффициенты φ , x, и h_с определяются экспериментально. Поскольку они взаимосвязаны, то, зная один из этих коэффици-ентов, можно определить любой другой по их соотношению

Для определения действительного расхода газа через сопло используется коэффициент расхода сопла µ:

^Gтеор

где G_i и G_теор – действительный и теоретический расходы газа через сопло.

Коэффициент µ определяется опытным путем. Он позволяет рассчитать, используя параметры идеального процесса истече-ния, действительный расход газа через сопло:

В свою очередь, зная коэффициент расхода µ, можно рассчи-тать коэффициенты φ и x для истечения газа через сопло. Запи-сав выражение (14) для одного из режимов истечения газа через сопло, получим соотношение

Отношения скоростей и объемов в формуле (16) можно выра-зить через отношение абсолютных температур идеального и реального процессов истечения:

^c1i = j = 1 - x , ^c1

_{где x =} ^T1i ^{- T}1 _. T_o - T₁

Подставив x = ^{T1i - T1} в выражение скоростного коэффици-T_o - T₁

ента, получим соотношение

Подставив выражения (17) и (18) в формулу (16), получим уравнение

В уравнении (18) одна неизвестная величина T_1i, которая мо-жет быть найдена как один из корней квадратного уравнения, полученного из выражения (19):

Преобразовав выражение (19а) и введя константу А, получим квадратное уравнение вида

Корни уравнения (19г) соответствуют выражению

В нашей задаче нужен только положительный корень, т.к. от-рицательных абсолютных температур не бывает. Поэтому рас-чет действительной температуры в конце процесса расширения ведется по выражению

Подставляя температуру Т_1i в выражение (18), рассчитываем скоростной коэффициент сопла φ. В свою очередь, коэффици-ент потерь сопла x находится по выражению (13) через скорост-ной коэффициент φ.

Не нашли, что искали? Воспользуйтесь поиском по сайту: