
|
|
ПРЯМОЕ И НЕПРЯМОЕ (КОСВЕННОЕ) ДОКАЗАТЕЛЬСТВО
Доказательства по форме делятся на прямые и непрямые (косвенные). Прямое доказательство идет от рассмотрения аргументов к доказательству тезиса, т. е. истинность тезиса непосредственно обосновывается аргументами. Схема этого доказательства такова: из данных аргументов(а, b, с...) необходимо следует доказываемый тезис q. По этому типу проводятся доказательства в судебной практике, в науке, в полемике, в сочинениях школьников, при изложении материала учителем и т. д. Широко используется прямое доказательство в статистических отчетах, в различного рода документах, в постановлениях, в художественной и другой литературе. Приведем пример прямого доказательства, использованного И. Буниным в стихотворении «В степи». А к нам идет угрюмая зима: Засохла степь, лес глохнет и желтеет, Осенний ветер, тучи нагоняя, Открыл в кустах звериные лазы, Листвой засыпал долы и овраги, И по ночам в их черной темноте, Под шум деревьев, свечками мерцают, Таинственно блуждая, волчьи очи... Да, край родной не радует теперь! Прямым является и такое доказательство. «Была жуткая ночь: выл ветер, дождь барабанил в окна. И вдруг среди грохота бури раздался вопль ужаса» (А. Конан Дойл). На уроке истории при прямом доказательстве тезиса «Народ — творец истории» учитель, во-первых, показывает, что народ является создателем материальных благ, во-вторых, обосновывает огромную роль народных масс в политике, в-третьих, раскрывает его большую роль в создании духовной культуры. На уроках химии прямое доказательство горючести сахара может быть представлено в форме категорического силлогизма: Все углеводы горючи. Сахар — углевод. _________________ Сахар горюч.
В современном журнале мод «Бурда» с помощью прямого доказательства тезис «Зависть — корень всех зол» обосновывается следующими аргументами: «Зависть не только отравляет людям повседневную жизнь, но может привести и к более серьезным последствиям, поэтому наряду с ревностью, злобой и ненавистью, несомненно, относится к самым плохим чертам характера. Подкравшись незаметно, зависть ранит больно и глубоко. Человек завидует благополучию других, мучается от сознания того, что кому-то более повезло». Непрямое (косвенное) доказательство — это доказательство, в котором истинность выдвинутого тезиса обосновывается путем доказательства ложности антитезиса. Если тезис обозначить буквой а, то его отрицание Апагогическое косвенное доказательство (или доказательство «от противного») осуществляется путем установления ложности противоречащего тезису суждения. Этот метод часто используется в математике. Пусть а — тезис (или теорема), который надо доказать. Предполагаем от противного, что а ложно, т. е. истинно не-а Следует заметить, что в конструктивной логике формула Примеров доказательства «от противного» очень много в школьном курсе математики. Так, например, методом «от противного» доказывается теорема: «Если две прямые перпендикулярны к одной и той же плоскости, то они параллельны». Доказательство этой теоремы начинается словами: «Предположим противное, т. е. что прямые АВ и CD не параллельны». Тогда они пересекаются и образуют треугольник с двумя внутренними прямыми углами, поэтому сумма всех трех внутренних углов треугольника больше 180°. Но это противоречит ранее доказанной теореме о том, что сумма внутренних углов любого треугольника равна 180°. Следовательно, наше предположение, что АВ и CD не параллельны, ложно, из чего (по закону исключенного третьего) вытекает доказанность теоремы о параллельности прямых АВ и CD. Разделительное доказательство (методом исключения). Антитезис является одним из членов разделительного суждения, в котором должны быть обязательно перечислены все возможные альтернативы, например:
Преступление могли совершить только либо Ау либо В, либо С. Доказано, что не совершали преступление ни Л, ни В. _______________________________ Преступление совершил С.
Истинность тезиса устанавливается путем последовательного доказательства ложности всех членов разделительного суждения, кроме одного. Здесь применяется структура отрицающе-утверждающего модуса разделительно-категорического силлогизма. Заключение будет истинным, если в разделительном суждении предусмотрены все возможные случаи (альтернативы), т. е. если оно является закрытым (полным) дизъюнктивным суждением.
Как ранее отмечалось, в этом модусе союз «или» может употребляться как строгая дизъюнкция (v) и как нестрогая дизъюнкция схемы (1 и 2).
ПОНЯТИЕ ОПРОВЕРЖЕНИЯ
Опровержение — логическая операция установления ложности или необоснованности ранее выдвинутого тезиса. Опровержение должно показать, что: 1) неправильно построено само доказательство (аргументы или демонстрация); 2) выдвинутый тезис ложен или не доказан. Суждение, которое надо опровергнуть, называется тезисом опровержения. Суждения, с помощью которых опровергается тезис, называются аргументами опровержения. Существуют три способа опровержения: 1) опровержение тезиса (прямое и косвенное); 2) критика аргументов; 3) выявление несостоятельности демонстрации.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 будет антитезисом, т. е. противоречащим тезису суждением.
будет антитезисом, т. е. противоречащим тезису суждением.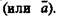 Из допущения а выводим следствия, которые противоречат действительности или ранее известным теоремам. Имеем
Из допущения а выводим следствия, которые противоречат действительности или ранее известным теоремам. Имеем 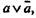 при этом а ложно, значит, истинно его отрицание, т. е.
при этом а ложно, значит, истинно его отрицание, т. е.  , которое по закону двузначной классической логики
, которое по закону двузначной классической логики  дает а. Значит, истинно а, что и требовалось доказать.
дает а. Значит, истинно а, что и требовалось доказать. не является выводимой, поэтому ею в доказательствах в конструктивной математике и конструктивной логике пользоваться нельзя; закон исключенного третьего также «отвергается» (не является выводимой формулой), поэтому косвенные доказательства там не применяются.
не является выводимой, поэтому ею в доказательствах в конструктивной математике и конструктивной логике пользоваться нельзя; закон исключенного третьего также «отвергается» (не является выводимой формулой), поэтому косвенные доказательства там не применяются. (1)
(1) поэтому ему соответствуют две логические
поэтому ему соответствуют две логические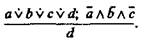 (2)
(2)