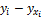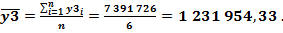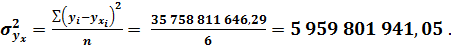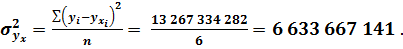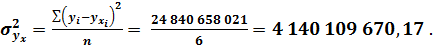|
|
б) Решение задачи для нелинейной связи показателей.12 Тесноту связи между исходными значениями параметров X и Y показывает корреляционное соотношение 𝛈 при нелинейной форме связи, определяемое по формуле:
где где Поэтому вначале необходимо определить выражение для уравнения регрессии, а затем уже определять тесноту связи между показателями, представленной уравнением второго порядка – параболы. Для нахождения коэффициентов параболы
Значения Параметры a, b и c находят способом определителей или способом исключения. Используем способ определителей. Определим недостающие для расчёта данные и сведём их в табл.17.4. Таблица 17.4 Промежуточные результаты для расчёта нелинейной связи показателей
Сначала найдём общий определитель: Определим выражение для общего определителя:
При таких значениях полученный результат, равный 3 920, можно считать ошибкой расчетов (за счет округлений), а значение определителя равным нулю. Поскольку общий определитель равен нулю (в большей степени, вследствие неточности расчётов и округлений – представления промежуточных результатов в натуральной форме), то вычислить коэффициенты a, b и c не представляется возможным. Следовательно, график функции не соответствует параболе. Воспользуемся априорным решением выражения (17.12) для вычисления коэффициентов a, b и c:
Определим значения коэффициентов с помощью уравнений (17.14 -17.17), при этом следует иметь в виду показатели: y1 – объём реализованной продукции (тыс.руб.); y2 – прибыль от реализованной продукции (тыс.руб.); y3 – затраты (себестоимость) на реализованную продукцию (тыс.руб.), и спрогнозируем изменение параметров y1, y2 и y3 в соответствии с полученными значениями a, b и c и выражением (17.2): по реализованной продукции:
Для прогнозирования объёма реализованной продукции получим функцию регрессии второго порядка:
Определим ожидаемые значения показателя объёма реализованной продукции в 2016, 2017 и 20185 годах:
по прибыли (убытку) от реализованной продукции:
Для прогнозирования прибыли (убытка) от реализации продукции получим функцию регрессии второго порядка:
Определим ожидаемые значения показателя прибыли (убытка) от реализованной продукции в 2016, 2017 и 2018 годах:
по затратам (себестоимости) на реализованную продукцию:
Для прогнозирования затрат (себестоимости) на реализованную продукцию получим функцию регрессии второго порядка:
Определим ожидаемые значения показателя затрат (себестоимости) на реализованную продукцию в 2016, 2017 и 2018 годах:
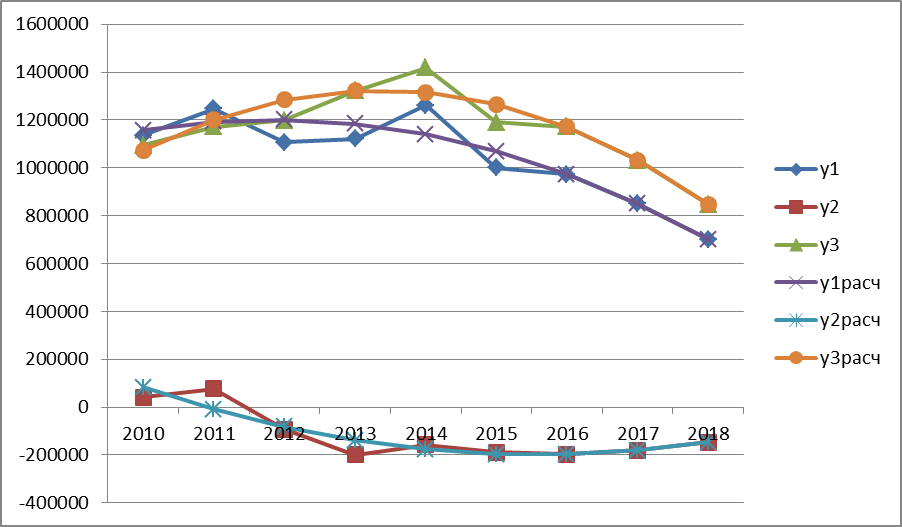
Построим графики функций регрессии при нелинейной связи показателей (рис.17.2).
Рис.17.2 – Графики функций выходных показателей на основе нелинейной связи. Определить тесноту связи показателей на основе корреляционного анализа. Корреляционное отношение η при нелинейной зависимости показателей определяется по формулам (17.10 и 17.11):
где Для определения значений тесноты связи рассчитаем значения промежуточных показателей и сведём их в табл.17.5. Таблица 17.5 Промежуточные результаты для расчёта тесноты связи показателей
Примечание: средние значения параметров были определены ранее и соответственно равны: • независимой переменной X (годы):
• зависимой переменной Y1 – реализованной продукции (РП):
• зависимой переменной Y2 – прибыли от реализации продукции (ПРП):
• зависимой переменной Y3 – затрат на реализованную продукцию (ЗТРП):
Расчётные значения вышеперечисленных параметров будем определять по формулам (17.2): • по реализованной продукции:
• по прибыли (убытку):
• по затратам (себестоимости):
Определим значения среднеквадратичных отклонений и корреляционного соотношения: • по объёму реализованной продукции:
• по прибыли (убытку):
• по затратам (себестоимости):

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (17.10)
(17.10)
 (17.11)
(17.11) - результативный показатель, рассчитанный на основе уравнения регрессии.
- результативный показатель, рассчитанный на основе уравнения регрессии. (17.2) решается линейная система из трёх уравнений:
(17.2) решается линейная система из трёх уравнений:
 (17.12)
(17.12)
 находят на основании исходных данных.
находят на основании исходных данных.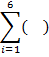
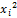






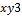

 . (17.13)
. (17.13)
 (17.14)
(17.14) или (17.15)
или (17.15) (17.16)
(17.16) (17.17)
(17.17)
 или
или

 .
.



 или
или
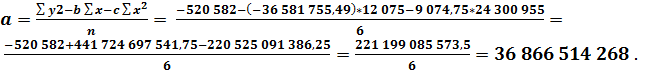
 .
.



 или
или
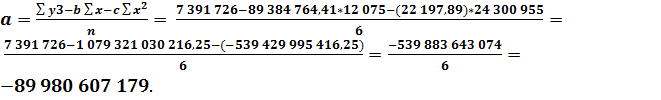
 .
.



 -
-