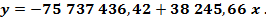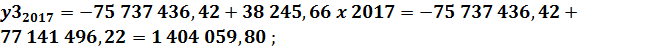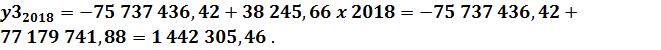|
|
Спрогнозировать изменение показателей на основе регрессионного анализа.12 Практическое занятие (3) к теме 17 Анализ и диагностика расходов и себестоимости продаж.
17.1. Метод корреляционно-регрессионного анализа (трендовый метод). Метод корреляционного и регрессионного анализа широко используется для определения тесноты связи между показателями, не находящимися в функциональной зависимости. Теснота связи между изучаемыми явлениями измеряется корреляционным отношением (для криволинейной зависимости). Для прямолинейной зависимости исчисляется коэффициент корреляции. Условие задачи. Выполнить оценку текущего состояния предприятия и перспективы экономических показателей в будущем на основе корреляционно-регрессионного (ретроспективного) анализа. Для этого выполнить: • корреляционный анализ взаимосвязи показателей деятельности предприятия; • прогнозирование показателей затрат и прибыли предприятия в 2016, 2017 и 2018 годах на основе регрессионного анализа с помощью: а) уравнения первого порядка: б) уравнения второго порядка: В учебных целях рассматривается период (2010 – 2015 годы) экономических показателей (реализованной продукции и прибыли) деятельности условного предприятия, выпускающее продукцию 6-и видов – комплектующие для других сборочных предприятий автомобильной промышленности (табл.17.1). Таблица 17.1 Общая характеристика товарной продукции предприятия
Построить графики показателей реализованной продукции, затрат (себестоимости) и прибыли предприятия в функции времени (годов выпуска), включая и три года (2016, 2017 и 2018 годы) планового периода. Подготовка дополнительных данных. Дополним исходные данные экономических показателей предприятия данными недостающих показателей затрат предприятия по годам выпуска:
где ЗТТП – затраты (себестоимость) реализованной продукции (тыс.руб.); РП – реализованная продукция (тыс.руб.); ПРП – прибыль (убыток) от реализованной продукции (тыс.руб.). Исходные и полученные данные показателей по годам деятельности предприятия обобщим в табл.17.2:
Таблица 17.2 Экономические показатели деятельности предприятия
Рассчитаем средние значения: • независимой переменной X (годы):
• зависимой переменной Y1 – реализованной продукции (РП):
• зависимой переменной Y2 – прибыли от реализации продукции (ПРП):
• зависимой переменной Y3 – затрат на реализованную продукцию (ЗТРП):
Решение задачи прогнозирования на основе корреляционно-регрес-сионного анализа. А) Решение задачи для линейной связи показателей. Определить тесноту связи показателей на основе корреляционного анализа. Тесноту связи между исходными значениями параметров X и Y показывает коэффициент корреляции r при линейной форме связи, определяемый по формуле:
Для расчёта коэффициента корреляции произведём необходимые для его определения расчёты недостающих показателей в табличной форме, где: x – год деятельности предприятия, y1 – реализованная продукция, y2 – прибыль от реализации продукции, y3 – затраты на реализованную продукцию (табл.17.3): Таблица 17.3 Промежуточные результаты для расчёта линейной связи показателей
Подставив соответствующие значения в формулу (17.8), получим: по реализованной продукции:
по прибыли (убыткам):
по затратам (себестоимости):
Как видно из полученных результатов, коэффициент корреляции имеет не очень высокие значения: -34,1% по реализованной продукции; -87,74% - по прибыли (убыткам); 61,34% - по затратам (себестоимости). Даже по полученным коэффициентам корреляции наблюдается определенная тенденция: снижения объемов реализованной продукции и полученной при этом прибыли (по отрицательным значениям соответствующих коэффициентов корреляции) и повышения затрат (себестоимости произведенной продукции) (по положительному значению коэффициента корреляции). Спрогнозировать изменение показателей на основе регрессионного анализа. Коэффициенты линейной регрессии
Определим значения коэффициентов a и b соответственно для каждого из трёх прогнозируемых экономических показателей предприятия: по реализованной продукции:
Функция регрессии: Определим ожидаемые значения показателя объёма реализованной продукции в 2016, 2017 и 2018 годах:
по прибыли (убытку):
Функция регрессии: Определим ожидаемые значения показателя прибыли (убытка) от реализации продукции в 2016, 2017 и 2018 годах:
по затратам (себестоимости):
Функция регрессии: Определим ожидаемые значения показателя затрат (себестоимости) реализованной продукции в 2016, 2017 и 2018 годах:
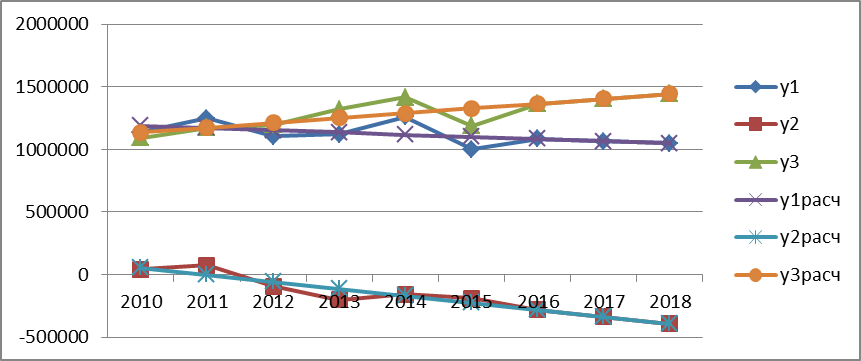
Построим графики функций регрессии при линейной связи показателей (рис.17.1).
Рис.17.1. Графики функций выходных показателей на основе линейной связи. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
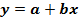 ; (17.1)
; (17.1) . (17.2)
. (17.2)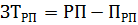 , (17.3)
, (17.3) (17.4)
(17.4)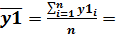 (17.5)
(17.5)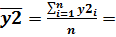 (17.6)
(17.6)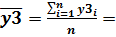 (17.7)
(17.7)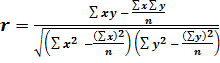 . (17.8)
. (17.8)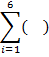
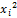
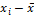

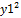
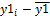


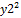
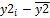




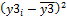
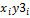

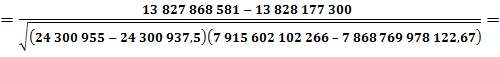

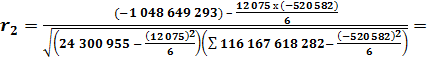 .
. 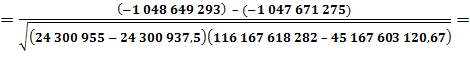
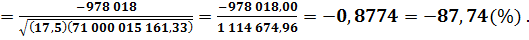
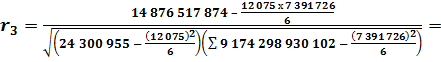 .
. 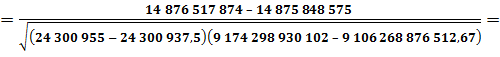
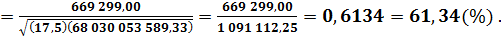
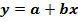 (17.1) вычисляются по следующим формулам (все суммы берутся по n парам исходных данных):
(17.1) вычисляются по следующим формулам (все суммы берутся по n парам исходных данных): (17.9)
(17.9)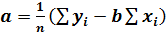 .
.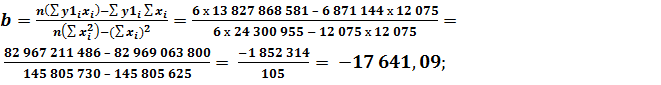
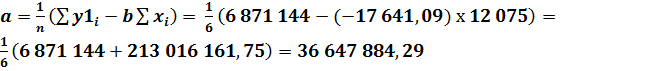 .
.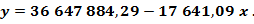

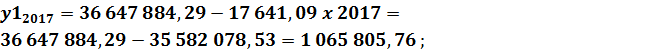
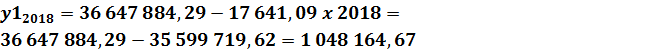 ;
;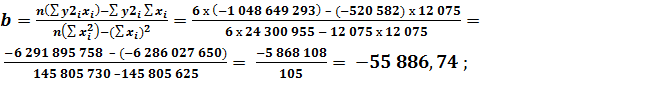
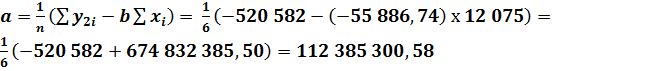 .
.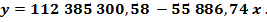
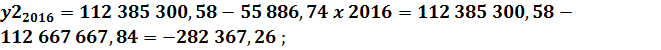
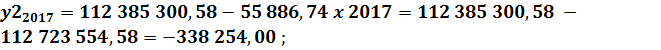
 ;
;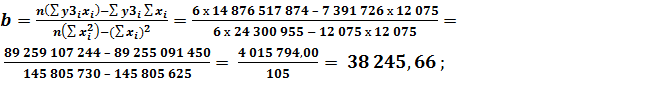
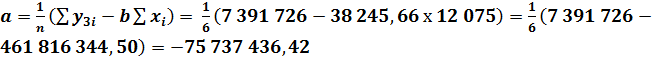 .
.