
|
|
Модели. Типы моделей и их использование12 Введение В предлагаемом курсе рассмотрены теоретические вопросы и алгоритмы решения типовых задач, необходимых для освоения тематики, с которой сталкиваются выпускники на профильных предприятиях. Материал не привязан к работе конкретных предприятий и это усложняет его изложение, так как не вводятся специфические исходные данные и изоусловия, которые всегда есть на предприятии и что позволяет осуществить решение задачи в необходимом для предприятия виде. Изложенные подходы как они изложены вообще, без изоусловий и специфики конкретной задачи, как правило, не работоспособны – это не их вина и составителя пособия, а специфика математических задач в необходимой для практики размерности. Они, как правило, некорректны, а изоусловия, как правило, и позволяют обеспечить регуляризацию задач. Этот комментарий нужен для того, чтобы правильно понимать место этих методов и компьютерных программ в структуре знаний и навыков. Это базовые представления о моделировании, оптимизации и идентификации. Более глубокое изучение применимости рассмотренных методов обсуждается в процессе курсового и дипломного проектирования, а также в учебных курсах аспирантов. Чтобы понять проблему выбора алгоритма устойчивого интегрирования 2-х точечной задачи, нужно эту задачу порешать, а это не очень-то быстрое занятие, даже имея стандартные математические пакеты для ЦВМ. Такие же и ещё большие проблемы и при решении задач идентификации, где обоснованность тех или иных алгоритмов во многом определяется и типом тестирующих сигналов когда доступны только сигналы «нормальной» эксплуатации, а не «оптимальной» для целей идентификации и выбраны алгоритмом управления в задачах адаптивного управления, доступной аппаратной базой для реализации законов управления и т.д. и т.п.. Ниже автор-составитель привел, по его мнению, минимально необходимый уровень знаний, навыков и ссылок, которыми должен обладать выпускник, чтобы приступить к осознанной деятельности по решению задач теоретических отделов приборостроительных предприятий. При этом автор-составитель исходил из учебных программ специальности 1903, в которых многие упоминаемые вопросы уже студентами до 5 курса, конечно в той или иной форме затрагивались. Здесь в первую очередь нужно указать, что абсолютно необходим уровень знания структуры цифровых САУ и программирования на языках: Ассемблер, чтобы понимать структуру подключения приборов ИУ к УВМ и оценивать динамику процессов управления, С++ максимально полно Microsoft Visual Studio, Fortran-как языка, наиболее просто транслирующего формулы. Явно видно, что математические библиотеки С++ есть перевод с Fortran.
Содержание Моделирование Моделирование сигналов и систем Моделирование динамических систем Моделирование случайных сигналов
Оптимизация Классические задачи на экстремум Линейное программирование Оптимальное управление
Идентификация 3.1. Идентификация систем ЛА 3.1.1. Параметрическая идентификация объектов 3.1.1. Идентификация в частотной области 3.2. Предварительная обработка исходной информации
Раздел 1. Моделирование Наблюдаемые нами явления и процессы в системах управления характеризуются множеством признаков, научная систематизация которых привела к структуре описания систем, которая математически представляет собой взаимосвязь между входными воздействиями и выходными координатами явлений и процессов. Так называемое Информационное описание процессов и явлений отстраняется от физической сущности процессов и направлено на выявление только моделей количественной взаимосвязи переменных, трактуемых как входные процессы с процессами, определяемыми как выходные. Таким образом математические модели /информационные/ системы являются упрощенным её описанием поскольку в них /моделях/ отражаются лишь некоторое подмножество свойств и признаков реальной системы. Для приборных систем основные задачи – это задачи достижения высоких точностных показателей и поэтому далее обсуждаются модели, связывающие сигналы входные как функции времени /либо их соответствующие изображения/ с выходными процессами в виде временных функций. Всё что нас окружает, оказывается, может быть с точки зрения количественной взаимосвязи процессов "вход-выход" описано с помощью нелинейных дифференциальных уравнений:
Входные сигналы, в общей постановке задач проектирования, тоже являются выходными процессами неких подсистем. В зависимости от степени изученности , управляемости и доступности этих подсистем говорят, что мы имеем дело с тремя типами сигналов (их моделями): 1. Детерминированные – т.е. сигналы, понаблюдав которые (в течение «разумного» времени), мы можем выявить алгоритм /формулу/ предсказания значения процесса в последующие моменты времени с «малой» погрешностью. 2. Индетерминированные – т.е. сигналы, наблюдение которых /пока?/ не позволяет указать алгоритм прогноза их эволюции по времени с «малой» погрешностью. 3. Случайные процессы – т.е. процессы, о значениях величины которых в некоторый момент времени точно сказать не можем, но можем дать оценки некоторых закономерностей и эти закономерности позволяют многие технические задачи решать с необходимой точностью.
Модели. Типы моделей и их использование
В технических приложениях необходимы такие модели, в которых соотношения, описывающие связи между системными переменными, задаются в виде разностных и дифференциальных уравнений. Математические модели могут быть снабжены набором поясняющих прилагательных (непрерывные и дискретные по времени, сосредоточенные и распределенные, детерминированные или стохастические, линейные или нелинейные и т.д.) в зависимости от типа используемых разностных или дифференциальных уравнений. Математическое моделирование является составной частью всех технических дисциплин. Основная задача техники заключается в том, чтобы используя математическую модель, найти хорошее проектно-конструкторское решение, которое соответствует экстремуму количественного показателя «хорошее решение», где переменные, входящие в показатель «хорошее решение», заданы через изоусловие «модель». /Эти задачи обсуждаются в разделе «Оптимизация»/. В процессе машинного моделирования моделью системы является программа Построение моделей опирается в основном на данные наблюдений. Существует два способа формирования математических моделей. Первый способ состоит в том, чтобы "расщепить" систему на такие подсистемы, свойства которых известны из ранее накопленного опыта. Это означает, что мы опираемся на соотношения, основанные на ранее проведенных экспериментальных исследованиях. Формальное математическое объединение этих подсистем становится моделью всей системы. При таком подходе проведение натурных экспериментов не обязательно. Основной прием сводится к структуризации процесса в виде блок-схем, блоки которых состоят из более простых элементов. В другом способе построения математических моделей непосредственно используются экспериментальные данные. В этом случае ведется регистрация входных и выходных сигналов системы, и модель формируется в результате обработки соответствующих данных. Этот способ называется идентификацией и рассматривается далее в разделе 3. Реальная система всегда отличается от построенной нами математической модели. Процесс идентификации приближает поведение технической системы и соответствующей математической модели, но никогда не сможем гарантировать их точного совпадения. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
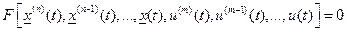
 - выходной сигнал (вектор размерности {n})
- выходной сигнал (вектор размерности {n}) - входной сигнал (вектор размерности {m})
- входной сигнал (вектор размерности {m})