Глава третья: Гармонические пирамиды на Земле и везде

САКРАЛЬНАЯ ГЕОМЕТРИЯ [1]

После того, как мы представили обзор единой модели эфира и раскрыли некоторые основы, как ведет себя жизнь на более ранних плотностях, мы будем рассматривать некоторые физические свойства этих плотностей и их эзотерические связи. И опять, важно помнить: эти плотности создаются жидкообразным нефизическим энергетическим источником. Убедительное обоснование существования жидкообразного “эфира” обширно и будет рассматриваться в деталях в томах 2 и 3.

Из источников, включая Ра, мы знаем: Вселенная представляет собой Одно. С одной стороны, Одно может приписываться Чистому Белому Свету. С другой, оно рассматривается как “Звук-Первоисточник” или ОМ. Затем мы говорили, что Одному стало скучно, ибо в Единстве никогда и ничего реально не менялось. Тогда из себя самого Одно решило создать новую жизненную форму. Чтобы это сделать, Одно завибрировало в “октаве”. Чистый Белый Свет стал набором семи цветов: красного, оранжевого, желтого, зеленого, голубого, индиго и фиолетового. Видимый цветовой спектр помнит об этом. Один Звук-Первоисточник распался на ряд чистых тонов - до, ре, ми, фа, соль, ля, си. Неизменная структура Октавы – ноты, являющиеся самыми чистыми математическими отношениями. Их лучше всего воспринимают наши уши. (Их можно видеть и слышать с помощью белых клавиш пианино.) Другое слово, обозначающее вибрации, – “гармоники”, и мы будем часто использовать его для описания этих систем.

Следует помнить: Чистый Белый Свет и Чистый Звук – два разных способа описания одних и тех же вибраций жидкообразной “разумной энергии” Одного. В действительности между ними нет разницы, ибо оба они – функции вибрации. Звук – вибрация молекул воздуха, свет – непосредственная вибрация жидкообразного эфира. В томе 2 мы увидим, что Дэйл Понд продемонстрировал следующее: если вы умножаете чистый звук много раз, то получаете частоты видимого света. Тем самым он доказал равенство между ними.

[Большинство ученых соглашается, что свет ведет себя как волна. Но, наряду с этим, они пытаются утверждать: не существует среды, в которой движется волна, и что волна – это просто похожая на частицу сущность, известная как “фотон”, движущийся в пустом “вакууме”. Это абсурдное замечание, ибо все естественные примеры волн имеют нечто, в чем они “волнятся”. Основное определение волны – “импульс, проходящий через среду”. И свет - не исключение.]

Третий ключ гармонического компонента, который следует иметь кроме света и звука, - геометрия – видимый результат вибрации. Первая и самая важная геометрия, с которой следует начать, - сфера. Древние традиции рассматривали сферу как высшую геометрию во Вселенной, чистую сущность Одного. В нашей физической модели Вселенная имеет форму сферы, ибо когда она формировалась, ее энергетические поля расширялись с постоянной скоростью во всех направлениях. [Все видимые галактики во Вселенной сходились в одну единственную “плоскую” супергалактику. Но даже в этой супергалактике все еще присутствуют сферические энергетические поля, хотя они и невидимы. Это будет обсуждаться в томе 3.] Сфера может быть сжата в одну точку, не имеющую ни времени, ни пространства и, следовательно, существует как самый простой объект во Вселенной. Но она же является самой сложной формой во Вселенной, содержащей внутри себя все другие вещи. Хотя поначалу может показаться, что вышесказанное не имеет смысла, его действительно просто объяснить, если начать с “плоской” двумерной демонстрации, чему и учились древние, изучающие священную геометрию.

Возьмем циркуль и нарисуем окружность. Любая крапинка на ней могла бы быть определена как точка. Затем вы можете взять линейку и из этой точки провести линию к любой другой возможной крапинке. Существует буквально бесконечное число линий, углов и форм, которые могли бы быть изображены в окружности. Математически говоря, никакая другая геометрическая форма не может образовывать внутри себя так много разных геометрий, как окружность. Следовательно, это самая сложная двумерная форма, какая только существует. В то же время, ее чистая гармоническая структура делает ее самой простой возможной двумерной формой во Вселенной. Это единственная форма, у которой одно ребро, нет прямых линий, а только кривая, совершающая полный оборот на 360 градусов вокруг единственной, центральной точки. Окружность превращается в Одно, и, следовательно, является самой простой возможной двумерной формой.

Расширяя эту форму в три измерения, мы можем видеть, что тот же самый принцип применим к сфере. А вот что сбивает с толку: физик Бакминстер Фуллер описывал сферу как “множество дискретных событий, приблизительно равно удаленных во всех направлениях от центрального ядра”. События, спросите вы? Выражаясь простым языком, вы можете вписать в сферу бесконечное число линий, связывающих бесконечное число точек (то есть, событий) на ее поверхности, причем все эти линии начинаются в одной единственной, центральной точке или ядре и имеют одинаковую длину. Это делает сферу самым сложным трехмерным объектом, который только существует; в нее можно вписать бесконечное число различных геометрических форм посредством простого соединения различных точек ее поверхности. Если вы любым образом растягиваете или сплющиваете сферу, то получаете меньше симметрии, и, следовательно, меньше гибкости в том, что геометрически может создаваться внутри. (Может показаться, что это трудно понять, но все можно доказать математически. Также, это объясняет, почему при свободном падении и/или в мыльном пузыре жидкость естественно формируется в сферы, ибо давление воздуха на жидкость одинаково со всех сторон.) По тем же причинам, что и окружность, сфера является самым простым трехмерным образованием во Вселенной. А именно: у нее только одна грань, совершенно симметричная в своей кривизне вокруг центральной точки. И снова все превращается в Одно. Для сравнения: куб имеет шесть сторон или граней, и является одной из самых простых трехмерных форм, которые только существуют. У сферы только одна “сторона”.

А вот что интересно: работа д-ра Ганса Дженни показала: когда жидкость в форме сферы вибрирует с чистыми “диатоническими” звуковыми частотами, то есть с основными вибрациями Октавы, внутри жидкости возникают геометрические формы. В ходе эксперимента крошечные частицы, известные как “коллоиды”, которые Дженни помещал в жидкость, собирались в основные геометрические формы, оставляя между собой чистую воду. В то время, как в обычных условиях эти частицы равномерно взвешены в воде. Когда д-р Дженни включал звуковую частоту высокого уровня, появлялись более сложные геометрические структуры. Когда он понижал звук до первоначального уровня, возникала та же самая геометрия, с которой он начинал. Эту убедительную демонстрацию можно видеть на видео д-ра Дженни “Профили”, которое доступно из различных источников. И все же научное сообщество в высшей степени недооценило и/или проигнорировало это исследование.

Таким образом, геометрия – самая основная характеристика вибрации; или, как когда-то говорил Пифагор: “Геометрия – это застывшая музыка”. Пять наиболее важных трехмерных геометрий, взятых вместе, известны как Платоновы Тела, ибо греческий философ Платон описал их первым.

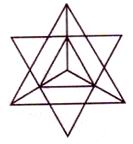
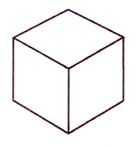
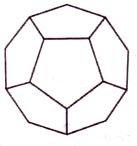
Октаэдр Звездный тетраэдр Куб Додекаэдр Икосаэдр

Рисунок 3.1 Пять Платоновых тел

Замечание: Звездный тетраэдр технически больше известен как сплетенный тетраэдр. Вы можете исследовать сам по себе тетраэдр – простую четырехгранную пирамиду, где каждая грань - равносторонний треугольник. Но в терминах активной энергии как вибрации, представляется, что большинство тетраэдральных структур являются двумя вставленными друг в друга тетраэдрами, как показано на рисунке выше.

Существует явное свидетельство того, что любое научное усилие, направленное на раскрытие важности этих геометрий во Вселенной, активно подавляется, ибо секретные братства все еще обладают огромной властью и полны решимости “всегда скрывать и никогда не раскрывать секреты Ордена”. Многие члены этих групп сознательно приходят к власти в различных научных институтах и используют свои руководящие посты, чтобы отклонять определенные виды исследований, особенно касающиеся свободной энергии/антигравитации; что мы будем обсуждать в томе 2. Ричард Хоагленд и Миссия Энтерпрайз, работая совместно с лейтенант-полковником Томом Бирденом, продемонстрировали, что такие усилия прослеживаются, по крайней мере, с 19-го века. Сэр Джеймс Клерк Максвелл – великий пионер 19-го века, анализировавший поведение электромагнитной (эм) волны. Его уравнения, известные как “кватернионы” (всего свыше 200 уравнений), использовались для отказа от рассмотрения скрытых внутренних структур эм волны в трехмерности. Анализируя все 200 кватернионов как группу, вы видите геометрию тетраэдра внутри сферы. Это скрытый секрет электромагнитной волны, основная структура, определяющая ее поведение при движении. Оливер Хэвисайд и другие свели уравнения Максвелла к четырем основным кватернионам и объявили скрытую геометрию “оккультной бессмыслицей”, решительно убрав ее из всех научных дебатов. Если бы не это, мы могли бы “решить головоломку” намного раньше.

Не существует прямого доказательства того, что члены секретных групп инспирировали политические нападки на работу Максвелла; но именно этого и следовало ожидать, основываясь на их системе верований, которую они поклялись защищать под страхом смерти. Еще один более очевидный пример: демонизация концепции “эфира”, используя в качестве “доказательства” результаты эксперимента Майкельсона-Морли. Мистик 19-го века мадам Блаватская предсказала, что эфир будет убран из обсуждения, и что “столпы науки с ним покончат”. Более подробно мы будем обсуждать это в томах 2 и 3. Даже сейчас предубеждение против эфира так сильно, что вас сразу же уволят, если вы попытаетесь поднять этот вопрос в научной дискуссии. Нас это не волнует, ибо время и доказательство залечат рану.

Как только мы принимаем существование жидкообразного эфира на разных уровнях плотности, где каждая плотность обладает своим качеством вибрации, мы сразу же осознаем, что в различных “чистых” вибрациях возникают определенные явные геометрические формы. Геометрия – единственный самый важный аспект поведения эфира в терминах его способности конструирования устойчивых структур, таких как кристаллы. Без геометрии материя была бы невозможна, ибо именно геометрия позволяет “пузырькам поля” собираться вместе в определенные организованные паттерны, образуя конкретные молекулы. В противном случае, самое большее, на что мы могли бы надеяться, - что сферы выстраивались бы полюс к полюсу или свободно плавали вокруг друг друга. А такое поведение недостаточно сложно для того, чтобы строить материю. Вершины геометрических форм обладают большей силой притягивать друг друга, чем другие области поверхности сферы (что мы будем обсуждать ниже). Это позволяет сферам организовываться в не случайные “матричные” паттерны.

Хотя большую часть времени мы не можем видеть эти геометрии, за исключением кристаллических структур, микрокластеров и квазикристаллов (том 3), они создают ярко выраженные “напряжения” или зоны давления в эфире, которые способны оказывать огромное влияние на свое окружение. Подумайте о силе, содержащейся в водовороте, и вы увидите, что внутри себя жидкость может иметь области более сильных и более слабых сил. Таким образом, геометрические формы обладают как качествами жидкости, ибо формируются в жидкой среде, так и кристалла, ибо они явно геометричны. Д-р Гарольд Аспден называет их “жидкими кристаллами”. К концу тома 3 у нас будет полная физическая модель для демонстрации того, как эти образования спрятаны во всей физике - квантовой, биологической или космологической. Если вы думаете, что химия и квантовая физика совершенны в той форме, в какой они существуют сейчас, то будете очень удивлены обнаружить, как много проблем существует в современных моделях, и что предлагаемый нами проект решает каждую из этих проблем. В этом томе мы коснемся некоторых основ влияния этого геометрического паттернирования, включая “Глобальную Решетку” энергетических линий на Земле, непосредственно формирующую континенты.

Самое важное качество Платоновых Тел: каждая форма совершенно вписывается в сферу так, что все их внешние вершины точно сливаются с внешней поверхностью сферы. Все прямые линии, составляющие эти объекты, будут одинаковой длины, а все геометрические точки на сфере равноудалены от своих соседей. Именно этого и следовало ожидать в науке о вибрации. Платон и другие греческие философы также указывали на то, что в этих геометрических телах все угловые измерения одинаковы, и что каждая грань трехмерных объектов имеет одну и ту же форму. Хотя поначалу это может сбивать с толку, в действительности все работает очень хорошо. Когда мы смотрим на эту информацию, мы видим, что соревнуются всего пять основных форм. Эти пять форм следующие: октаэдр (восьмигранник), звездный тетраэдр (два четырехгранника, вставленные друг в друга), куб (шестигранник), додекаэдр (двенадцатигранник) и икосаэдр (двадцатигранник).

Чтобы понять, почему эти геометрические объекты образуют вибрирующую сферу жидкообразной энергии, следует кое-что знать о волновом движении. Если у нас есть простая двумерная волна, например, гитарная струна, то существуют три основных компонента, которые будут оставаться неизменными, если волна не возмущается. Это длина волны, частота и амплитуда. Длина волны – это насколько велика каждая часть волны, то есть, “наблюдаемое расстояние между двумя соседними гребнями волны”; в случае видимого света измеряется как линейная величина в ангстремах. Частота – количество гребней волны, которые проходят перед наблюдателем в каждую секунду; измеряется как число колебаний в секунду или в “герцах”. Амплитуда – насколько высока каждая волна, то есть, “величина волны, измеренная от нуля до пика”.

Любой цвет или звук, остающиеся неизменными какой-то период времени, все это время будут непрерывно повторять волны одинаковой длины. Типичный пример: “концертный уровень” частоты ноты ля 440 колебаний в секунду. Это значит: когда воздух вибрирует 440 раз в секунду, наше ухо интерпретирует это как музыкальных звук “ля”. Только и всего. Если бы не все 440 колебаний имели одинаковые частоту и амплитуду, мы бы не воспринимали устойчивую высоту в устойчивом объеме. Если мы повышаем частоту звука, например, до 497 колебаний в секунду, то повышается высота, а длина волны становится короче. Если мы увеличиваем амплитуду, увеличивается объем звука, увеличивается высота волны, а высота звука останется той же.

Также следует помнить: в этих волнах может храниться сложная информация. У нас есть два вида радиоволн: частотная модуляция или ЧМ и амплитудная модуляция или АМ. Слово “модуляция” означает “изменение”. Итак, в качестве простого объяснения: ЧМ волны имеют одинаковую амплитуду, но непрерывные изменения (модуляции) частоты, в то время как АМ волны имеют одинаковую частоту, но непрерывные изменения амплитуды. Вот в основном и все. Поскольку волны могут двигаться очень быстро, в них может храниться огромное количество информации; и это очень важное положение. В любой момент нас окружают АМ/ЧМ радио, Би-Би-Си, частоты полиции/пожарной службы/аварийной службы, радио-, теле- и спутниковые станции, беспроволочные и сотовые телефонные разговоры.

Далее, когда внутри сферы присутствует трехмерная геометрическая волновая форма, длина волны и частота будут представлены расстоянием между различными узловыми точками на поверхности сферы. Они могут измеряться в градусах и вычисляться посредством синусной тригонометрической функции. Амплитуда будет измеряться размером сферы, в радианах, и вычисляться с помощью косинусной функции. Таким образом, как только мы увеличиваем интенсивность (амплитуду) энергетического поля сферы, увеличиваются размеры самой сферы. Это объясняет, почему такие структуры существуют в размерах от самого крошечного уровня квантовой механики и до известной Вселенной. Также важно осознать: в жидкообразной системе эфира повышения частоты будут втягивать внутрь сферы энергию из окружающей среды. Следовательно, происходит увеличение размеров (амплитуды) сферы, и одна геометрия сдвигается в другую. В этой главе мы будем исследовать это позже, когда увидим, как четко разные Платоновы Тела “гнездятся” внутри друг друга, причем каждая новая геометрия больше, чем находящаяся внутри нее. Характерно, что повышение частоты вовлекает в процесс и увеличение амплитуды.

Единственное, что осталось объяснить: почему на поверхности сферы вибрации образуют точки или вершины с соединяющими их прямыми линиями. Вернувшись к простому объяснению волны в двух измерениях, известному как волновая механика, мы узнаем, что каждая волна имеет определенные точки, известные как “узлы”, где нет движения. Легче всего это увидеть на примере основной синусоидальной волны - медленно движущейся волны на поверхности озера – непрерывная S-образная кривая. Если вы дернете гитарную струну, в ней существуют определенные области, где совсем нет никакого движения; эта часть струны будет оставаться в абсолютном покое. Такие области называются “узлами”. Мы наблюдаем длину волны, измеряя расстояние между узлами. Также узел можно рассматривать как область, где детские качели удерживаются металлическим столбом; любая сторона качелей может идти вверх и вниз, но середина доски всегда будет находиться в одном и том же месте. В волновой механике такая точка известна как “узел” или “точечный момент”.

Аналогично, точечные концы или вершины Платоновых Тел представляют собой узлы волны. Они находятся там, где во всей сфере создается наименьшее количество вибрации. В результате мы видим, что в “точках спокойствия” концентрируется огромная энергия, создаваемая давлением окружающих их точек. Узловые области (так же как и центр сферы) обладают самой большой энергетической интенсивностью на всей поверхности сферы, ибо окружающие их зоны высокого давления будут естественно собирать и направлять все “свободное” в зоны точек с низким давлением. Именно по этой причине в эксперименте д-ра Дженни в узлах собирается самое большее число свободных “коллоидов”. (По этой же причине в атмосфере штормовые облака с высоким давлением плывут в зоны низкого давления.) Поскольку в соответствии с законами вибрации узлы сильно давят друг на друга, старая поговорка гласит: “Кратчайшее расстояние между двумя точками – прямая линия”. Поэтому, как только формируются узлы, между ними сразу же возникают силовые линии. И когда мы наблюдаем все линии вместе, появляется геометрический объект, просто как результат соединения точек.

И последние термины волновой механики, которые сейчас необходимо ввести: “движущаяся волна” и “стоячая волна”. (Также используются термины “динамическая” или “распространяющаяся” для движущейся волны и “статическая” для стоячей волны.) Объяснение понятно из названия: движущаяся волна движется в пространстве. Стоячая волна, вибрируя, остается в покое. Итак, если у нас есть сфера жидкости, которая остается неизменной и обладает внутри себя геометрическим паттерном напряжения, такая геометрия имеет отношение к “стоячей волне”. Как только мы думаем в этих терминах, становится легко сложить всю модель; она основана на простых известных физических принципах вибрирующей жидкости и псевдотвердых “напряжениях”, которые благодаря вибрации могут формироваться внутри нее.

ГЕОМЕТРИЧЕСКИЕ ФОРМЫ, СООТВЕТСТВУЮЩИЕ “ПЛОТНОСТЯМ”

Если мы мысленно вернемся к идее существования во Вселенной Октавы эфирных плотностей, то увидим, что эти плотности обладают цветом, звуком и геометрическими компонентами. Конечно, это наиболее часто изучаемая связь, которую исследовали наследники древних мистерий. Она изучалась достаточно долго после того, как они утеряли след полного объема стоящего за ней научного знания. Поэтому самая первая головоломка, над которой мы работали с 1996 по 1998 годы, была: “Какую геометрическую форму мы приписываем каждой из семи основных плотностей; ибо можно работать только с пятью Платоновыми Телами и сферой?” Нам и не нужны восемь форм, ибо древние традиции говорят, что и в начале и в конце Октавы находится сфера. Аналогично, в звуковой Октаве каждая нота, на октаву выше, чем другая, будет звучать одинаково, просто в другом регистре – в высшей или низшей октаве. Математически, любая музыкальная нота, находящаяся на октаву выше, будет иметь вдвое большее число колебаний в секунду. Отсюда, “ля” с 440 колебаниями в секунду снова станет “ля” с 880 колебаниями в секунду.

Итак, где же седьмая форма? Как утверждает бесценная книга Роберта Лолора Сакральная геометрия, ответ был обнаружен в Индии, в “религиозных мифах” древних священных книг Веды, наследников империи Рама. Индусы или их контакты дали ответ, предложив одно из Платоновых Тел дважды. Аналогично тому, как сфера появляется дважды – в начале и конце октавы, то же самое делает ближайший к ней гармонический партнер – икосаэдр, расположенный на втором и седьмом уровнях плотности. В богатой мистической культуре древних ведических текстов, благодаря тесному сотрудничеству с летающими в легендарных виманах инопланетными сущностями, форма икосаэдра реально превратилась в бога. Они называли его Пуруша. И в седьмом измерении или плотности он представлял собой мужскую силу во Вселенной.

Рисунок 3.2 Икосаэдр, известный как мужской бог “Пуруша” в древней империи Рама

Как мы только что сказали, Пуруша также демонстрирует первую форму, кристаллизующуюся в сфере, когда мы находимся в начале спектра. Следовательно, Одно, будучи проявлением всех сознательных сущностей, должно выкристаллизовываться в мире форм как Пуруша; и любая сущность должна снова достичь уровня Пуруши, чтобы вернуться к Одному в конце цикла. Нижеследующий рисунок из Сакральной геометрии Лолора показывает, как вы можете нарисовать двумерный икосаэдр, используя циркуль и линейку.

Рисунок 3.3 Икосаэдр, нарисованный в двух измерениях циркулем и линейкой

Перед тем, как заявлять, что индийская культура страдала женофобией, управлялась мужчинами и приписывала мужественность всем самым лучшим духовным силам в жизни, осознайте, что Ян дополнялся Инь. Универсальная женская сила известна как Практити и определяется как додекаэдр или шестая плотность.

Рисунок 3.4 Додэкаэдр, известный как женская богиня “Практити” в древней империи Рама

Фактически, представляется, что каждая плотность может рассматриваться как обладающая либо “мужскими”, либо “женскими” качествами: вторая плотность – женская, третья – мужская, четвертая – женская, пятая – мужская и так далее. Давайте не будем забывать, что Единство – это комбинация обоих полов в Единении. Таким образом, поскольку во второй плотности Пуруша начинается как женщина, мы видим, что он Отец/Мать бог, включающий в себя женский архетип или Практити. Когда мы продвинемся в проектировании и понимании метафизических и духовных свойств измерений, их “пол” приобретет в высшей степени хороший смысл. Помимо сферы, мы можем видеть, что Пуруша и Практити – две самые высшие формы в спектре. Поэтому в некотором роде имеет смысл, что эти две формы могли олицетворять как богов, так и богинь. Высшие сферы – явно нечто, к чему мы можем стремиться. Они – сознательные формы.

Наш современный дом пребывает в форме номер 3. Октаэдр – это вибрационный уровень, обеспечивающий основную невидимую структуру энергии, из которой созданы все наши атомы и молекулы. Род Джонсон, чья сакральная геометрическая модель квантовой физики рассматривается в томе 3, утверждает, что наблюдаемые в лаборатории, не обладающие массой “нейтрино” вполне могли бы быть октаэдрами. Однако чаще всего эти вибрации останутся необнаруженными, ибо являются только основной структурой реальности, а не самой действительной реальностью. Когда вы смотрите на законченный небоскреб, вы не видите двутавровых балок. Аналогично, мы не видим “энергию нулевой точки”, создающую “виртуальные частицы” - протоны, нейтроны и электроны, которые непрерывно появляются и исчезают из существования. Тем не менее, мы знаем, что они должны существовать. Таким образом, древняя физика учит: эта форма представляет собой фундаментальную основу всей материи в нашей “плотности”. Это забытое древнее учение. Важно осознать, что это только общее правило, ибо внутри нашей плотности мы видим все Платоновы Тела, представляющие различные “подплотности”. Чтобы построить физическую материю, нам нужны они все. Но самая сильная форма в третьей плотности – октаэдр.

Рисунок 3.5 Октаэдр – основная геометрия “третьей плотности”

Если посмотреть на верхнюю половину октаэдра, можно легко заметить, что она идентична форме египетской Великой Пирамиды. При наличии физической модели, этот факт явно демонстрирует то, что все пирамиды были построены для фокусирования геометрической энергии эфира, как воронки в потоке воды. Как мы увидим позже в этом томе, “торсионные поля” на Земле могут варьироваться от места к месту намного больше, чем нормальные “напряжения” или магнитное поле Земли. На русском профессиональном жаргоне любая пирамида действует как “пассивный торсионный генератор”.

Сама материя ведет себя как погруженная в воду вибрирующая губка. Пульсирующим движением жидкообразная энергия непрерывно втекает и вытекает из нее. Когда вы собираете материю в единую структуру, форма этой структуры будет определяться тем, как сквозь нее текут эфирные потоки. Любой цилиндрический или конический объект будет захватывать и фокусировать спиралевидно выходящие из Земли торсионные поля, а коническая форма может фокусировать и направлять эти поля. Давайте не забывать, что они состоят из разумной энергии; и одно из главных преимуществ овладения этими полями в том, что они очень быстро будут значительно улучшать ваше физическое здоровье и духовное сознание. Отсюда, древние египтяне считали пирамиды “храмами посвящения”. И мы знаем, что греческое слово “Пирамида” - синтез двух слов: “Пире” и “Амид”, что означает “Огонь в Середине”. “Огонь в середине” - это энергетические поля, фокусирующиеся внутри Пирамиды. То есть, само название маскирует в себе часть секрета.

При наличии истинной науки мы осознаем, что Великая Пирамида в Гизе – самая точно спроектированная пирамида на Земле, фантастическая машина, возведенная технологией, намного превосходящей современный научный уровень понимания. Причина, почему это так, - технология сознания, уже закончившего разработку физической модели, которая только сейчас вновь выходит на публичную арену. И чем больше мы исследуем Пирамиду, тем яснее видим, каким точным и исчерпывающим должно было быть входящее в нее знание.

Рисунок 3.6 Великая Пирамида совершенно вписывается в полусферу

Вот признанный и давно известный факт: если вы возьмете отношение между основанием и высотой Пирамиды, то получите отношение 960 – 3,14159. Это значит, что из центра пирамиды вы можете нарисовать окружность через один из ее углов; и если вы продлите ее вверх и вниз до противоположного угла, то эта окружность будет касаться всех трех точек. Тогда, все, что следует делать, - думать в трех измерениях; и мы быстро откроем, что Пирамида математически совершенно вписывается в полусферу (см. на рисунке выше).

Итак, пирамидальная структура самым непосредственным образом входит в резонанс с эфиром, вынуждая формироваться вокруг себя сферу невидимой энергии. Помните, что самая сильная геометрическая энергетическая структура нашего измерения, если бы мы могли ее увидеть, выглядела бы точно как пирамида. Следовательно, пирамида была не только геометрическим объектом, она была построена как гигантская застывшая “единица сознания”. На одном уровне, мы могли бы думать о ней как о гигантской статуе в честь энергетической плотности, которую мы сейчас населяем, на другом – как об очень эффективной машине. Ра говорил: когда пирамида была построена, она работала намного эффективней, чем сейчас. Снижение эффективности произошло благодаря изменению местонахождения Земли и изнашиванию ее каменных граней.

Многие специалисты по пирамидам указывали на то, что внутри пирамиды посредством различных измерений изображается точная длина Земного года – 365,2422 дней. Как только ученые поняли, что Пирамида совершенно вписывается в полусферу, они пришли к выводу, что она предназначалась для представления Земли. Но это не объяснило бы, почему строители пирамид просто не возвели шар, особенно с имеющейся в их распоряжении очевидной технологией для точного расположения таких огромных камней. И только сейчас мы можем видеть, почему для выражения Земли была выбрана форма октаэдра.

Хотя сейчас мы не можем видеть пирамиду как кристалл, в египтологических кругах это хорошо известный факт: когда пирамида была построена, снаружи ее полностью покрывала облицовка. Облицовка была сделана из белого туранского известняка, отполированного до зеркального блеска (Лемесурье, 1977). Днем пирамида сияла так ярко, что ослепляла; отсюда древние египтяне называли ее “Та Кут” или “Свет”. Смотря на эту оригинальную форму, очень легко прийти к выводу, что ее построили не примитивные человеческие существа. На рисунке мы видим остатки этих камней, еще сохранившиеся у основания пирамиды.

Рисунок 3.7 Облицовочные камни, сохранившиеся вдоль периметра основания Великой Пирамиды

А вот нечто, что зачастую неизвестно: промежутки между камнями облицовки составляют всего 1/100 дюйма (Лемесурье, Хоагленд). Для сравнения: самое лучшее, что смогла сделать современная технология для соединения экранирующих тепло плиток на космическом корабле Шаттл – 1/30 дюйма (Хоагленд). Это поднимает способ соединения облицовочных камней на уровень оптической точности; нечто, что мы бы использовали только для крайне чувствительных частей оборудования. Такая точность использовалась для того, чтобы сделать пирамиду намного более эффективной в качестве “машины” для овладения торсионными полями.

Более того, в невероятно крошечных пространствах между камнями облицовки, таких крошечных, что между ними нельзя просунуть даже лезвие ножа, находится невероятно тонкий слой “цемента”, удерживающий их вместе. Этот “цемент” так прочен, что если ударить по нему кувалдой, скорее разрушится сам известняк, чем “цемент”. Вплоть до сегодняшнего дня никто не представил убедительного объяснения, как это могло быть сделано. Определенно представляется, что сами камни были сплавлены, и, следовательно, цемента не было совсем. А возникшее образование – всего лишь результат крайне высокой температуры, сплавившей два камня вместе. Тогда, как они получали такую температуру? Может быть лазер? Или сфокусированное сознание, преобразующее материальный аспект сознательных молекул известняка? По мере углубления в его модель, объяснения Ра обретают для нас все больший и больший смысл: они могли использовать сознание для визуализации того, как им хотелось, чтобы располагались камни. Затем визуализация стала реальностью.

Рисунок 3.8 Вид сверху второй пирамиды на плато Гизы, демонстрирующей облицовочные камни наверху.

Резюмируя: внешний вид Пирамиды был создан с такой оптической точностью, что сейчас его можно увязать только с работой, которую мы делаем для зеркальных линз отражающего телескопа (Хоагленд). Теперь мы можем себе представить гигантскую пирамиду, построенную из четырех зеркал, днем сияющую так ярко, что почти ослепляющую. И снова, не удивительно, что древние египтяне относились к ней как к “Та Кут” или Свету. Когда пирамида находилась в своем истинно кристаллическом состоянии, не возникало сомнений в том, что она была построена не людьми того времени, а инопланетной структурой. Сейчас мы можем только представлять ее изначальный внешний вид, ибо землетрясения сотрясали облицовочные камни, они откалывались в начале первого тысячелетия новой эры, и затем эти совершенные белые камни растаскивались для строительства мечетей в Каире. Следовательно, мы можем измерять первоначальный проект этих камней, пользуясь несколькими из них, сохранившихся у основания и все еще неповрежденных. Верхушка второй пирамиды тоже сохранила несколько облицовочных камней (см. рисунок выше).

Такая почти ненормальная степень точности начинает обретать намного больший смысл, когда мы осознаем, какими энергиями можно было овладеть посредством сооружения такой структуры. Эти энергии не могли быть холодными и безжизненными, как электричество; напротив, они представляли собой сознательную энергию, а, следовательно, могли управляться подготовленным сознательным человеческим существом. Наряду с Ра и чтениями Кейси, собственные источники автора указывают на то, что человек, хорошо подготовленный для управления этой энергией, мог омолаживать умирающие тела до ранней молодости и жизнестойкости, путешествовать во времени и, посредством левитации легко передвигать массивные объекты. Более того, пирамида помогала стабилизировать Землю по ее осям, смягчать суровую погоду и землетрясения в окружающей ее местности, исцелять и приводить в норму ум, очищать воду, создавать энергию и устранять остаточную радиацию от атомных войн за намного более короткий срок. Чем больше мы узнаем о вовлеченной в строительство пирамид науке, тем более очевидным это становится, и с тем большим желанием нам следует снова восстановить всемирную сеть пирамид для исцеления Земли от современных созданных нами разрушений [2].

Ра рассказывает: Пирамида была гигантским даром, который они создали для нашей цивилизации; даром, изначальной целью которого было создание храма для посвящения. Также она функционировала как эффективный балансирующий фактор для энергетических полей Земли. Наличие “храма посвящения” означало, что можно было овладеть энергиями более высокого уровня, интегрировать их в физические и нефизические тела исследователей, и, пребывая на Земле, духовно развиваться, проходя через спектр семи плотностей. Это очень жестокий и вселяющий страх процесс, ибо человек оказывался лицом к лицу одновременно со всеми “искажениями” личностного я, что приводило к длительным ночным кошмарам. Подготовленный целитель, способный выходить из тела вместе с пациентом, когда они отправлялись в путешествие, всегда присутствовал при выполнении этой работы, ибо один только страх мог заставить человека потерять след физического тела и, следовательно, умереть.

Не нашли, что искали? Воспользуйтесь поиском по сайту: