
|
|
Определение срока проведения операции (по сложной ставке ссудных процентов). Финансовые функции в ППП EXCEL (КПЕР)12
Воспользуемся формулой
Из последнего равенства получим
Аналогично можно получить формулы для вычисления сроков оплаты платежа по номинальной годовой ставке j:
откуда получим
Логарифмы находятся по специальной таблице или вычисляются на калькуляторе. Но существует 2 специальных правила, позволяющих рассчитать срок удвоения первоначальной суммы для конкретного процентной ставки. правило «72» => правило «69» => Эти правила получены из формулы (2.4.1) с учетом того, что первоначальное значение Эти правила дают довольно точный результат при наибольших значениях процентных ставок. При процентной ставке до 100 % отклонения достаточно малы, и ими можно пренебречь. При процентной ставке 120 % погрешность по правилу «69» составляет 5,2%, а для правила «72» будет еще больше и будет расти с ростом процентной ставки. При этом срок удвоения, полученный по правилу «69» будет больше, чем в действительности, а по «72» меньше. Пример 1. Найти срок удвоения капитала при годовых ставках: А=20%, В=110%. Решение. По формуле (2.4.1) и по правилам «69» и «72» найдем: 1) а) б) в) 2) а) б) в) Ответ.При годовой процентной ставке 20 % срок удвоения капитала может составлять 3,6 и 3,8 года; для В=110 % срок удвоения капитала может составлять 0,93, 0,98 и 0,65 года.
Для определения сроков проведения финансовой операции в ППП EXCEL предусмотрена функция КПЕР: КПЕР(ставка; ;нз;бс;[тип]). Эта функция рассчитывает общее число периодов начисления процентов, необходимых для того, чтобы настоящая сумма НЗ достигла указанной БС.
Пример 2. Рассчитать, через сколько лет вклад 1 000 000 достигнет величины 1 000 000 000 денежных единиц, если годовая процентная ставка по вкладу составляет 16,79. И начисление процентов производится ежеквартально. Решение. КПЕР Ответ.Через 42 года вклад достигнет заданной величины. Пример 3. За какой срок первоначальный капитал в 50 000 000 денежных единиц увеличится до 200 000 000 денежных единиц, если: а) на него будут начислены сложные проценты по ставке 28% годовых; б) проценты будут начисляться ежеквартально по номинальной процентной ставке. Решение. а) б) m - число интервалов начисления, j=0,28. Ответ.а) 5,6 года; б) 5,1 года. Пример 4. Какова должна быть сложная процентная ставка ссудного процента, что бы первоначальный капитал утроился за 5 лет? Решить пример так же для случая начисления процентов по полугодиям по номинальной процентной ставке. Решение.а) б) Ответ.а) сложная процентная ставка, при которой первоначальный капитал утроиться составляет 24,5 %; б) номинальная процентная ставка, при которой первоначальный капитал утроиться составляет 23,2 %. Упражнения
Упражнение 1.Первоначальная сумма составляет 850 тыс. денежных единиц. Определить наращенную сумму через 6,5 года по ставке 13 % годовых: 1) по простой процентной ставке (нарисовать график зависимости величины FV от n); 2) по сложной процентной ставке, если проценты начисляются непрерывно (нарисовать график зависимости величины FV от n). 3) по сложной процентной ставке, если проценты начисляются два раза в год (нарисовать график зависимости величины FV от n). 4) для случая 3 показать эффективную и номинальную ставки, сделать вывод. Упражнение 2.Найти наращенную сумму, если первоначальная сумма составляет 363 565,50 денежных единиц, начисление процентов происходит ежеквартально на протяжении 11 лет и 2 месяцев по сложной процентной ставке равной 15% годовых. С помощью функций ППП EXCEL решить следующие задачи: Расчеты на основе постоянной процентной ставки. Функция БС Значения переменных указаны в таблице 2.5.1 Упражнение 3. Сумма размером X тыс. денежных единиц положена на счет под Y % годовых на Z лет. Рассчитайте, какая сумма окажется на счете, если проценты начисляются ежеквартально. Упражнение 4.Рассчитайте, какая сумма будет на счете, если вклад размеромA тыс. денежных единиц размещен подB % годовых наZ лет, а проценты начисляются каждые полгода. Упражнение 5.По вкладу размеромX тыс. денежных единиц начисляетсяC% годовых. Рассчитайте, какая сумма будет на сберегательном счете черезD лет, если проценты начисляются ежедневно. Упражнение 6.Определите будущую величину вклада в E денежных единиц, помещенного в банк на 8 лет под Y % годовых если начисление процентов осуществляется: а) раз в году;б) раз в полгода; в) раз в квартал; г) раз в месяц. Упражнение 7.Клиент, располагая суммой E денежных единиц, намерен положить деньги в банк сроком на G гда F месяца. В банке существуют 2 типа вклада: «РОСТ» с процентной ставкой 12 % годовых, начисляемых ежемесячно, «ПРОЦЕНТ» – со ставкой 13 % годовых, начисляемых ежегодно. Какой из двух вкладов более выгоден клиенту?
Таблица 2.5.1
Определение текущей стоимости. Функция ПС Значения переменных указаны в таблице 2.5.2. Упражнение 8.В настоящее время фирма располагает деньгами и готова положить их на депозит единым вкладом, чтобы черезZ лет он достигXтыс. денежных единиц. Определим необходимую сумму текущего вклада, если ставка процента по нему составляетY % в год. Упражнение 9.Рассчитайте текущую стоимость вклада, который через B года составит С тыс. денежных единиц при начислении D % в год. Упражнение 10.Рассчитайте, какую сумму необходимо положить на депозит, чтобы через Z года она достигла значения E млн денежных единиц при начислении A % годовых. Упражнение 11.Рассчитайте текущую стоимость вклада, который через Z лет составитG тыс. денежных единиц при начислении F% годовых. Начисление осуществляется: а) 1 раз в год; б) 1 раз в полгода; в) 1 раз в квартал; г) 1 раз в месяц. Таблица 2.5.2
Функции БЗРАСПИС, ЭФФЕКТ, НОМИНАЛ Значения переменных указаны в таблице 2.5.3. Упражнение 12.Рассчитайте будущую (наращенную) стоимость облигации номиналомA тыс. денежных единиц, выпущенной на B лет, предусмотрен следующий порядок начисления процентов: в первый год – C %, в два последующих года – D %,в оставшиеся года – E %, по сложной процентной ставке. Упражнение 13.Рассмотрим заем в X тыс. денежных единиц с номинальной нормой процента С % и сроком уплаты B года. Пусть весь заем и начисленные на него проценты будут выплачены единой суммой в конце этого срока. Какая сумма будет выплачена, если начисление процентов: а) полугодовое; б) квартальное; в) месячное; г) ежедневное. Упражнение 14.Допустим, эффективная ставка составляет Q, а начисление процентов производится: a) ежемесячно; б) ежеквартально в) ежедневно. Рассчитать номинальную ставку. Таблица 2.5.3
Расчеты. Функция СТАВКА Значения переменных указаны в таблице 2.5.4. Упражнение 15.По вкладу X денежных единиц, помещенному в банк на Y года, по истечении срока проведения операции было выплачено Z денежных единиц, определите годовую процентную ставку. Упражнение 16.Какой должна быть годовая процентная ставка по вкладу размером A тыс. денежных единиц, если его величина к концу года составит B тыс. денежных единиц, а проценты начислялись ежемесячно. Упражнение 17.Рассчитайте процентную ставку для 3-летнего займа (проценты начислялись ежеквартально) размером С млн денежных единиц если к концу срока действия договора о займе объем выплаты достигнет В млн денежных единиц. Таблица 2.5.4
Расчеты. Функция КПЕР Значения переменных указаны в таблице 2.5.5. Упражнение 18.По вкладу в X денежных единиц, помещенному в банк под Y % годовых была выплачена сумма Zденежных единиц Определите количество периодов начисления процентов. Упражнение 19.Рассчитать через, сколько лет вклад размером Aмлн достигнет величины B млрд. денежных единиц, если годовая ставка процента по вкладу C % и начисление процентов производится: а) ежемесячно; б) ежегодно. Таблица 2.5.5
Упражнение 20.Определить количество периодов начисления процентов по вкладу X ден. ед. помещенному в банк, если под 18 % годовых выплачена сумма Z ден. ед. а) проценты начислялись 1 раз в год; б) проценты начислялись 1 раз в месяц.
Тест к теме «Cложные ставки ссудных процентов» Начало формы 1) В каких финансовых кредитных операциях применяются сложные процентные ставки?
[1] Везде далее говорится о финансовых функциях MicrosoftOfficeExcel 2003. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
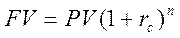 . Прологарифмируем обе части равенства
. Прологарифмируем обе части равенства ,
,
 . (2.4.1)
. (2.4.1)
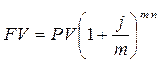 ,
,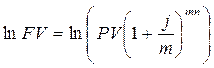 ,
, ,
, . (2.4.2)
. (2.4.2) ;
;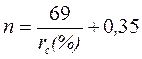 .
. ,
, 

 (года);
(года); (года);
(года); (года).
(года).
 (года);
(года); (года);
(года); (года).
(года). =168 (кварт.). Число лет равно 168:4=42 годам.
=168 (кварт.). Число лет равно 168:4=42 годам. (года);
(года);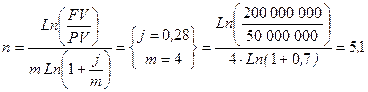 (года);
(года);
