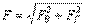|
|
Пьезометрическая высота. Вакуум. Измерение давления
где Отсюда высота подъема жидкости в пьезометре где ризб — избыточное давление на уровне присоединения пьезометра. Часто Давление в жидкостях или газах численно выражают в виде соответствующей этому давлению пьезометрической высоты по формуле (2.9). Если абсолютное давление в жидкости или газе меньше атмосферного, то говорят, что имеет место разрежение, или вакуум. За величину разрежения, или вакуума, принимается недостаток до атмосферного давления: (вакуумметр) Основное уравнение гидростатики Потенциальная, удельная энергия жидкости.
Сократив все члены уравнения на dS, получим:
Давление во всех точках свободной поверхности одинаково и равно р0, следовательно, давление во всех точках жидкости на глубине h также одинаково согласно основному уравнения гидростатики. Поверхность, давление на которой одинаково, называется поверхностью уровня. В данном случае поверхности уровня являются горизонтальными плоскостями. Выберем некоторую горизонтальную плоскость сравнения, проходящую на расстоянии z0 от свободной поверхности, тогда можно записать уравнение гидростатики в виде:
Все члены уравнения имеют линейную размерность и носят название: - геометричкская высота,
Величина 12 Сила давления жидкости на плоские и кривые поверхности
Выразим сначала элементарную силу давления, приложенную к бесконечно малой площадке где Для определения полной силы где Следовательно,
или те полная сила давления жидкости на плоскую стенку равна произведению площади стенки на гидростатическое давление Кривая поверхность
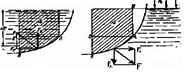
1) жидкость расположена сверху 2) жидкость расположена снизу В первом случае выделим объем жидкости, ограниченный рассматриваемой поверхностью АВ, вертикальными поверхностями, проведенными через границы этого участка, и свободной поверхностью жидкости, т. е. объем ABCD, и рассмотрим условия его равновесия в вертикальном и горизонтальном направлениях. Условие равновесия объема ABCD в вертикальном направлении имеет вид FB = p0SГ + G где Условие равновесия того же объема в горизонтальном направлении запишем FГ=SBρghC+p0SB Определив по формулам (1.31) и (1.32) вертикальную и горизонтальную составляющие полной силы давления
Понятие о движении жидкости как непрерывной деформации сплошной материальной среды Кинематика жидкости является разделом гидромеханики, в котором движение изучается вне зависимости от действующих сил; в кинематике устанавливаются связи между геометрическими характеристиками движения и временем. Идеальной жидкости, т. е. такая воображаемая жидкость, которая совершенно лишена вязкости. В такой невязкой жидкости, так же как и в неподвижных реальных жидкостях, возможен лишь один вид напряжений — нормальные напряжения сжатия, т. е. гидромеханическое давление, или просто давление.
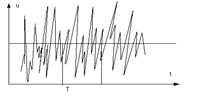
Давление в движущейся идеальной жидкости обладает теми же свойствами, что и в неподвижной жидкости, т. е. на внешней поверхности жидкости оно направлено по внутренней нормали, а в любой точке внутри жидкости — по всем направлениям одинаково. Ламинарные течения жидкости могут быть установившимися (стационарными) или неустановившимися (нестационарными). Турбулентные течения всегда являются неустановившимися; хаотическое движение частиц в турбулентном потоке создаёт резкие изменения местных скоростей во времени, называемые пульсациями скорости. U=1/T S, 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

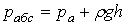 .
.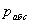 — абсолютное давление в жидкости на уровне присоединения пьезометра;
— абсолютное давление в жидкости на уровне присоединения пьезометра; 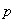 — атмосферное давление.
— атмосферное давление.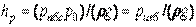 )
)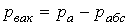 или
или 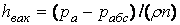
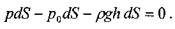
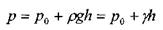
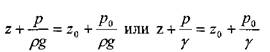
 - пьезометрическая высота
- пьезометрическая высота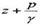 носит название гидростатического напора.
носит название гидростатического напора.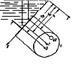
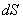 :
: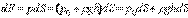
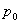 — давление на свободной поверхности;
— давление на свободной поверхности;  — глубина расположения площадки
— глубина расположения площадки 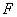 проинтегрируем полученное выражение по всей площади
проинтегрируем полученное выражение по всей площади 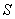 :
: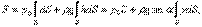
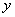 — координата площадки
— координата площадки 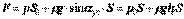
 (здесь
(здесь 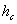 — глубина расположения центра тяжести площади S.),
— глубина расположения центра тяжести площади S.),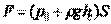
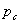 в центре тяжести этойплощади.
в центре тяжести этойплощади.