|
|
Информационные системы и технологии на транспорте12 ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА Федеральное Государственное Бюджетное образовательное учреждение высшего профессионального образования «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ» (МИИТ)
Одобрено кафедрой «Теоретическая и прикладная механика» ИНЖЕНЕРНАЯ И КОМПЬЮТЕРНАЯ ГРАФИКА Часть 2 Задания и методические указания По выполнению контрольной работы для студентов 1 курса Направление: Информационные системы и технологии на транспорте Профиль: Информационные системы и технологии на транспорте
РОАТ
Москва 2014
ОБЩИЕ УКАЗАНИЯ Контрольная работа по разделу курса - проекционное черчение включает 3 задания, которые выполняются студентами на трёх форматах A3 карандашом с помощью чертёжных инструментов по государственный стандартам трёхсотой группы (ГОСТ 2.300 - 68). Основная надпись должна быть оформлена по ГОСТ 2.104 - 68. ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ: НФ - непроизводная фигура; СФ - составная фигура; ПП - параметр положения; ПФ - параметр формы; П - параметрическое число; ПК - персональный компьютер; СК - система координат.
@ Российский государственный открытый технический университет путей сообщения, 1999
1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ НА ПЛОСКОСТИ ( ЗАДАНИЕ 1 ) Задание № 1 по инженерной графике связано с геометрическими построениями на плоскости и выполняется (см. рис.1) с учетом общих правил геометрического конструирования фигур и единого оформления чертежа, предусмотренных ГОСТ 2.301-307-68,81. Поскольку объектом рассмотрения являются двумерные (плоские) фигуры, изображаемые на плоском чертеже, то для выполнения работы не требуется знаний раздела курса "Проекционное черчение". Напомним, что в последнем изучаются правила построения изображений трехмерных (объемных) фигур на плоскости чертежа. В задании № 1 необходимо выполнить: 1. Геометрический анализ плоской СФ с целью выявления составляющих ее НФ; 2. Построение НФ, заданных полным и неполным набором параметров с учетом геометрических условий; 3. Построение точек сопряжения НФ и выполнение самих сопряжений; 4. Рациональное базирование фигуры (задание базовой СК) и определение минимального достаточного количества проставляемых размеров с учетом геометрических условий взаимоотношений НФ в СФ. Перечисленные задачи решаются с помощью теории параметризации [1,2] , как единой методической базы, отвечающей на основные вопросы формирования и чтения чертежа любой фигуры (плоской либо пространственной). Задание выполняется на формате A3 (420 х 297 мм). Все построения сохраняются, являясь тонкими линиями ( ~ 1/3 S), где S - основная контурная линия. Каждая точка сопряжения должна быть построена пересечением двух линий - контура фигуры и одной из линий построения. Размеры проставляются по мере выполнения геометрических построений, как это рекомендовано в разделе 1.3. Геометрические построения на чертеже можно проводить с помощью простейших чертежных инструментов (циркуля, линейки, угольника) на формате чертежной бумаги, а также на экране ПК с помощью набора команд с клавиатуры и устройства типа "мышь"
Рис.1
При этом алгоритмы геометрических построений и в том, и в другом случаях одинаковы и включают последовательность некоторых графических операций построения вспомогательных элементов сопряжения НФ в структуре СФ [2].
К элементарным геометрическим построениям относятся графические операции, связанные с делением отрезка прямой на заданное число равных частей, построением и делением углов на равные части, проведением параллельных и перпендикулярных прямых, делением окружностей и построением правильных многоугольников и т.д. Перечисленные алгоритмы описаны в [3] и могут быть при необходимости дополнительно изучены студентами. Рассмотрим более подробно нетривиальные алгоритмы геометрических построений, необходимые для выполнения первого задания контрольной работы.
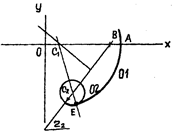
1.1. ОСНОВНЫЕ ГРУППЫ АЛГОРИТМОВ ГЕОМЕТРИЧЕСКИХ ПОСТРОЕНИЙ Первая группа алгоритмов связана с построением точек взаимного сопряжения двух окружностей и сопряжения двух окружностей прямой при заданных радиусах и координатах их центров. 1.1.1. Сопряжение двух окружностей (рис.2), заданных пятью параметрами (П-5). Наборы параметров могут быть различными, например, 4ПП - координаты двух центров и 1ПФ - радиус, или ЗПП и 2ПФ. Алгоритм построения точки сопряжения основан на построении линии центров окружностей и отыскании на ней точки касания с засечкой одним из радиусов ( R1 Ú R2 ). Алгоритм построения реализуется независимо от характера касания -внешнего либо внутреннего. 1.1.2. Сопряжение двух окружностей прямой. Представленная на рис. 3 СФ обычно задается параметрическим числом 6П (4ПП + + 2ПФ), связанным с окружностями, и геометрическим условием касания (внешнее, внутреннее), воспринимаемым с чертежа "на глаз". 1.1.2.1. Внешнее касание связано с построением точек А и С. Алгоритм построения: в С1 строим окружность радиуса (R1 – R2) и точку G (0,5С1С2 ); из точки G -строим половину окружности радиуса R =
1.1.2.2. Внутреннее касание связало с построением точки В и D аналогично случаю внешнего касания. Отличие заключается в построении в центре C1 вспомогательной окружности суммарного радиуса ( R1 + R2 ). Дальнейшая часть алгоритма аналогична приведенной выше (рис.3). 1.1.2.3. Частным случаем алгоритма (1.2.1) является задача проведения касательной к окружности (ЗП) из данной точки (2П) - рис.4,
Рис.4 Рис. 5 Вторая группа алгоритмов связана с построением сопряжений двух прямых окружностью заданного либо неизвестного радиуса при фиксированной точке на одной прямой. Данная система имеет параметрическое число 5П (4ПП+1ПФ). 1.2.1.Сопряжение двух прямых окружностью заданного радиуса R (рис.5). Из произвольной точки прямой а восстанавливаем перпендикуляр ( h ^ а ), на котором откладываем отрезок AD = R (заданный радиус). Проводим прямую l || a. Аналогичные построения повторяем для прямой b . Из точки О опускаем два перпендикуляра на прямые а и b . Точки К и N являются искомыми точками сопряжения прямых а и b окружностью радиуса R с центром О. 1.2.2. Сопряжение двух прямых (n, m) дугой окружности в заданной точке Е одной из прямых (рис.6).
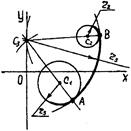
Строим биссектрису l угла, составленного заданными прямыми. Из точки Е восстанавливаем перпендикуляр до пересечения с биссектрисой l . Точка С1 является центром сопрягающей окружности. Точка В получена тривиальными построениями. Третья группа алгоритмов для решения наиболее сложных задач на построение точек сопряжения и центров окружностей с нетривиальными исходными данными. 1.3.1. Задана точка А окружности 01 (рис.7). В точке А задано направление диаметра, то есть определен один параметр положения. Вторая окружность 02 полностью определена (ЗП). Требуется построить сопряжение окружностей. Касание внутреннее. Решение. Из точки А на оси ОХ откладываем отрезок АВ = r2. Из центра отрезка C2В проводим перпендикуляр до пересечения с осью ОХ. Точка пересечения С1 есть центр окружности 01. Проводим линию При построении точки сопряжения двух окружностей внешнего касания (рис.8) точку В строим справа от точки А. Остальная часть алгоритма не меняется. 1.3.2. Внешнее сопряжение двух заданных окружностей 01,02 третьей, заданной одним параметром формы r3, - рис.9.
Решение. Из заданных центров окружностей C1,C2 строим дуги суммарных радиусов (r1+r3 ) и (r2+r3). На их пересечении строим центр окружности 03.Точки сопряжений А и В лежат на линиях центров С1С3 , С2,С3 При внутреннем сопряжении центр С3 строим на пересечении радиусов (r3- r1) и (r3 - r2) – рис.10.
 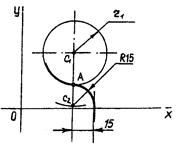
1.3.3. Ряд алгоритмов связан с построением параметров сопряжения попарных окружностей, заданных различными наборами параметров и геометрическими условиями, например сопряжение, представленное на рис.11. 1. 2. АНАЛИЗ ЗАДАНИЯ И ПОРЯДОК ЕГО ВЫПОЛНЕНИЯ
Каждому варианту задания соответствует геометрическая фигура - плоский контур, составленный из НФ. Исходные данные представлены в таблице 1 вариантов (см. ниже). Каждая строка таблицы содержит координаты опорных точек 1.2.1. Порядок выполнения работы 1.2.1.1. Анализ фигуры по следующей схеме: а) определение количества осей симметрии (одна или две); б) оценка по результатам п.1,а половины или четверти фигуры; в) выбор направления обхода данной части контура и вычисление количества параметров для каждой НФ с учетом геометрических условий. 1.2.1.2. Задание базовой системы координат на чертеже из условий минимизации числа параметров. В отдельных вариантах базовая система координат совпадает с исходной, в которой реализовано задание исходных данных. 1.2.1.3. Реализация алгоритма построения контура на формате. Все построения выполняются в базовой системе координат. На поле чертежа по заданным координатам строятся опорные точки контура ( А , В , ...). Далее проводятся окружности, заданные полным набором параметров (ПП=2; Ш-I; П=3) , и от- --------------------------- См. Приложение.
ТАБЛИЦА ВАРИАНТОВ ЗАДАНИЙ 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

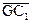 =
= 

 =
=  .
.