Компонентный анализ в среде StatGraphics

Для проведения расчетов в среде StatGraphics нужно занести данные на электронный лист, например, скопировать через буфер обмена с листа Excel. Лучший вариант – сохранение данных в формате листа Excel ранних версий. Рассмотрим ключевые этапы работы для примера с морфологической изменчивостью гадюк.

Открыть в среде StatGraphics файл следует командой меню или кнопкой Open Data File.

Чтобы имена переменных, назначенных в Excel, автоматически становились именами столбцов, они должны даваться латиницей; в окошке запроса отметить, что имена переменных в первом ряду есть.

Результаты экспорта данных можно посмотреть в окне данных, специально распахнув окно иконки, лежащей на сером поле слева в нижнем углу.

Запустить программу компонентного анализа можно только командой меню Special\ Multivariate Methods\ Principal Components.

Выбрав мышкой имена нужных переменных, кнопкой Data: их нужно скопировать в правое окно, ОК. Для дальнейшей идентификации объектов, их метки следует поместить в окно Point Labels:.

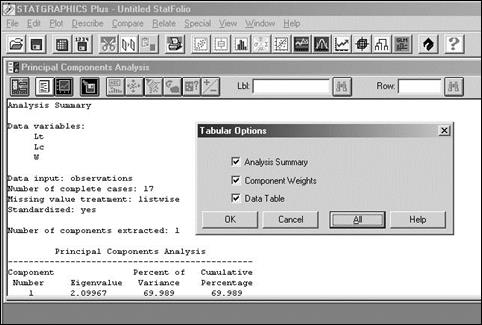
В появившемся окне Principal Component Analysis четыре кнопки играют важную роль. Первая слева кнопка Input Dialog позволяет вернуться на предыдущий шаг и переопределить список анализируемых переменных. Кнопка Tabular Options обеспечивает доступ ко всем результатам анализа (All, OK). Окно Analysis Summary выводит значения дисперсий главных компонент, окно Table of Component Weights дает значения факторных нагрузок, в окно Table of Principal Components выведены значения главных компонент.

Кнопка Graphical Options раскрывает окна с графическими иллюстрациями (All, OK).

Все окно результатов компонентного анализа предстает в виде десяти небольших окошек; распахнуть любое из них позволяет двойной клик левой кнопкой мыши.

Полнота результатов вычислений во многом определяется установками в окне Principal Components Options, которое вызывается командой контекстного меню Analysis options… (правый клик на любом окне анализа). Минимально необходимый объем информации появляется, если в блоке Extract by … Number of Components задать число 2 (т. е. выводить результаты для двух компонент); кроме того, можно задать иное минимальное значение дисперсии главной компоненты (Eigenvalue), чем принятое по умолчанию значение 1. В результате на графиках и в таблицах будут отображаться данные по компонентам, дисперсия которых превышает заданный уровень.

Диаграмма факторных нагрузок (Plot of Component Weights) копирует таблицу Table of Component Weights и призвана наглядно представить степень коррелированности соответствующих признаков.

График Scree Plot отражает изменение дисперсий компонент и (пунктиром) минимальный уровень значимых компонент.

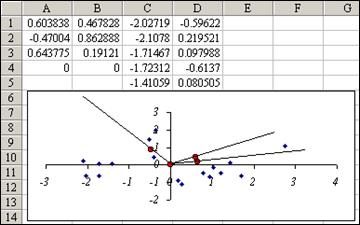
Наиболее интересна диаграмма Scatterplot, где представлена ординация объектов в осях компонент,

а также Biplot, где к диаграмме Scatterplot добавлена диаграмма Plot of Component Weights в форме лучей.

Каждый из этих лучей построен по двум опорным точкам: в месте пересечения осей компонент (0,0) и в точке с координатами факторных нагрузок двух первых компонент (a_1j,a_2j) (здесь j – номер соответствующего признака). Это возможно потому, что и компоненты, и факторные нагрузки есть безразмерные признаки. Биплот наглядно показывает направления изменчивости данных, за которые ответственны определенные признаки. По промерам гадюк видно, что первое направление изменчивости (выявленное первой главной компонентой) определяет отличие особей по массе (W) и длине тела (Lt), а второе (вторая компонента) связано в основном с отличиями по длине хвоста (Lc).

Результаты расчетов можно поместить на электронный лист (с помощью кнопки Save results, поставив галочки в нужных окошках), через буфер обмена скопировать на лист Excel, и воспользоваться его богатыми графическими возможностями.

В частности, чтобы понять принцип построения биплота, следует объединить (копированием) две точечные диаграммы, построенные раздельно по значениям главных компонент и факторных нагрузок, соединив лучами точки нагрузок с пересечением осей.

10

Имитационное моделирование в среде Excel

Вообще говоря, любая мысль об окружающем мире есть его модель. Имитационная модель – это компьютерная программа, которая служит для количественного отображения поведения реальных объектов в разных условиях. Смысл построения имитационных моделей состоит, во-первых, в том, чтобы установить (выразить уравнением) количественные закономерности протекания явлений природы, во-вторых, – оценить модельные параметры (коэффициентов пропорциональности между переменными уравнений). Параметры моделей часто имеют биологический смысл, поскольку выражают существо отношений между характеристиками объектов исследования.

Моделирование пока не столь широко распространено, как того требуют сложные задачи современной биологии, особенно экологии. На наш взгляд, одним из препятствий этому служит распространенное мнение, что "полноценными" могут быть лишь дающие прогноз аналитические модели; сопряженные с этим сложности построения системы дифференциальных уравнений и их решения оказываются серьезным препятствием для большинства биологов. Однако изучаемые экологические явления сначала нужно понять, дать им объяснение, а уж затем, при необходимости, и прогнозировать.

Мы предлагаем давать количественное объяснение с помощью имитационного моделирования – составлять модели, основанные на простейших (линейных) алгебраических уравнениях, и определять значения их параметров посредством внешних процедур "оптимизации".

Вместо составления и решения дифференциальных уравнений предлагается составлять программы и настраивать параметры имитационных моделей. Обе эти проблемы оптимально решаются в среде пакета Microsoft Excel.

Способ построения моделей на листе Excel отличается от традиционных способов программирования (алгоритмического, структурного или объектного) – это табличное программирование. На листе Excel модель предстает в всех своих деталях, как таблица, ячейки которой заполнены формулами, имитирующими либо выборку вариант (статические модели), либо ход процесса (динамические модели). Каждая ячейка содержит формулу, которая вычисляет соответствующее "модельное" значение варианты или характеристику системы на очередном временнóм шагу. Поскольку "объяснительные" значения модельных переменных должны более или менее совпадать с реальными наблюдениями, организуется процедура поиска таких (оптимальных) значений модельных параметров, которые делают отличия между моделью и реальностью наименьшими, минимизируют "функцию отличий", или "функцию невязки". Эта процедура оптимизации выполняется с помощью отдельной программы "Поиск решения", встроенной в пакет Excel. (Ответственное отношение к моделированию требует понимания существа процедуры настройки! [см.: Коросов, 2002]).

Помимо программирования самой модели и настройки ее параметров требуется доказать значимость модельных параметров, адекватность модели. Для решения этой задачи на листе Excel приходится конструировать целую имитационную систему, состоящую из следующих компонентов:

· блок исходных данных, зачастую состоящий из массива независимых и зависимых переменных;

· блок расчета модельных данных, собственно имитационная модель, состоящая из уравнений; осуществляет расчет явных переменных и скрытых переменных;

· блок параметров, участвующих в расчете модельных данных и изменяемых в процессе настройки;

· блок расчета отличий реальных и расчетных значений переменных;

· значение суммы отличий между моделью и реальностью (значение функции невязки); оно минимизируется в процессе настройки;

· блок процедуры настройки (программа "Поиск решения");

· блок графического представления результатов;

· блок статистической оценки результатов.

В результате несложных действий мы получаем очень гибкий инструмент описания действительности. В потенциях имитационной модели стать сложной и детализированной или, напротив, простой и обобщающей, выражающей законы, управляющие миром.

Не нашли, что искали? Воспользуйтесь поиском по сайту: