
|
|
Коэффициенты ковариации и корреляции12 Для двух активов Для инвестирования капитала лишь в актив одного вида необходимо, чтобы из всех имеющихся на рынке активов он бы л наилучший, т.е. его ожидаемый риск (дисперсия) был наименьшим, а ожидаемая доходность наибольшей. Что же должен делать инвестор, если такого актива на финансовом рынке не существует? В этом случае выгоднее выбрать не один актив, а несколько стремясь перераспределить (диверсифицировать) риск с целью уменьшения его количественной оценки. Степень возможности такой диверсификации зависит от характеристики, служащей мерой связи между случайными величинами, представляющими доходности активов. Речь идет о ковариации. Дадим ее определение коэффициента ковариации для двух дискретных случайных величин. Пусть заданы две дискретные случайные величины своими
При
Отметим, что
Пример 3.1. Ежемесячные доходности акций PEPSIиMOBIL за 1987 год приведены ниже. Найти коэффициенты ковариации и корреляции. PEPSI - MOBIL - -0.682, -0.267, 9.115 Решение Найдем средние ожидаемые доходности, ожидаемый риск и среднеквадратическое отклонение для каждой акции по формулам (2.1), (2.2), (2.3). Получим значения
Найдем значения
9.115-0.731
Cуммируя полученные значения и деля сумму на N-1=12-1=11 получим 1.8464, т.е.
Коэффициент корреляции вычисляем по формуле (3.2.)
Ответ: Коэффициент ковариации - 1.8464, корреляции - 0.23957. 4. Пакет активов и способы его задания Пусть на рынке имеются различные активы и известны статистические данные для каждого актива, представляющие собой временные ряды доходностей за последовательные периоды в прошлом. Напомним, что доходность за период вычисляется исходя из начальной и конечной цены актива и текущего дохода за период (см. пункт 1.). Для каждого актива можно вычислить его характеристики: среднюю ожидаемую доходность (2.1), дисперсию (2.2), среднеквадратическое отклонение (2.3). Для каждой пары активов можно вычислить коэффициенты ковариации (3.1) и корреляции (3.2). Инвестор из имеющихся активов выбирает те, в которые он собирается вложить свой инвестиционный капитал. Такой набор активов имеет и другое название - пакет активов. В пакет активов будут входит различные активы имеющиеся на рынке, характеристики которых известны. Пусть вектор средних - матрица ковариации - матрица корреляции - где Матрицы ковариации и корреляции симметрические матрица, т. к Итак для задания пакета достаточно задать вектор средних пакета Пример 4.1. Найти характеристики пакета составленного из акций PEPSIиMOBIL за 1987 год. Решение Положим, что актив коэффициент ковариации - 1.8464, т.е. Используя эти результаты получаем матрицу ковариации пакета
Коэффициент корреляции - 0.23957, поэтому матрица корреляции
Ответ: матрица корреляции пакета - Задачи Имеется пакеты акций 4.1. {AMEX, CBS},4.2.{EXXON, CBS},4.3. {EXXON, AMEX}.Найти характеристики этих пакетов. Доходности за 1987 год приведены ниже. AMEX: 20.088, 8.824, 1.02, -8.403, -0.917, 2.044,7.664, 0.678, -3.367, -32.223, -7.254, 2.235 CBS: 9.941, 15.846, -5.435, 7.553, -0.458, 8.166, 11.325, 3.903, 11.619, -23.533, -9.558, 1.046 EXXON: 18.004, -4.199, 9.41, 1.02, 1.472, 7.184, 0.938, 6.906, -2.384, -12.339, -12.610, 3.741

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
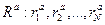 ,
,  . Обозначим их ожидаемые значения
. Обозначим их ожидаемые значения  соответственно. Тогда коэффициентом ковариации случайных величин
соответственно. Тогда коэффициентом ковариации случайных величин 
 называют величину
называют величину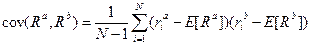 . (3.1)
. (3.1) получаем
получаем .
. . На ковариацию оказывает влияние не только связь между случайными величинами, но и их дисперсии. Чтобы выделить меру собственно связи между случайными величинами прибегают к нормированию ковариации. Такая нормированная величина называется коэффициентом корреляции
. На ковариацию оказывает влияние не только связь между случайными величинами, но и их дисперсии. Чтобы выделить меру собственно связи между случайными величинами прибегают к нормированию ковариации. Такая нормированная величина называется коэффициентом корреляции . (3.2)
. (3.2)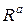 : 19.712, 6.827, 3.489, -6.569, 9.375, 3.343, 8.333, 0, 2.359. -14.78, -8.487, 8.21
: 19.712, 6.827, 3.489, -6.569, 9.375, 3.343, 8.333, 0, 2.359. -14.78, -8.487, 8.21 : 3.194, 2.952, -8.178, -17.812, -15.046, 15.926, 9.346, -2.165, 12.389,
: 3.194, 2.952, -8.178, -17.812, -15.046, 15.926, 9.346, -2.165, 12.389, .
. ,
, 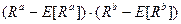
 : 19.712-2.651, 6.827-2.651, 3.489-2.651, -6.569-2.651, 9.375-2.651, 3.343-2.651, 8.333-2.651, 0-2.651, 2.359-2.651. -14.78-2.651, -8.487-2.651, 8.21-2.651
: 19.712-2.651, 6.827-2.651, 3.489-2.651, -6.569-2.651, 9.375-2.651, 3.343-2.651, 8.333-2.651, 0-2.651, 2.359-2.651. -14.78-2.651, -8.487-2.651, 8.21-2.651 : 3.194-0.731, 2.952-0.731, -8.178-0.731, -17.812-0.731, -15.046-0.731, 15.926-0.731, 9.346-0.731, -2.165-0.731, 12.389-0.731, -0.682-0.731, -0.267-0.731,
: 3.194-0.731, 2.952-0.731, -8.178-0.731, -17.812-0.731, -15.046-0.731, 15.926-0.731, 9.346-0.731, -2.165-0.731, 12.389-0.731, -0.682-0.731, -0.267-0.731,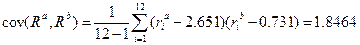 .
.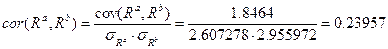
 - пакет из n различных активов. Пусть доходность каждого актива
- пакет из n различных активов. Пусть доходность каждого актива  (i=1,2,...,n) - случайная величина
(i=1,2,...,n) - случайная величина  . Будем обозначать характеристики этой случайной величины -
. Будем обозначать характеристики этой случайной величины -  (средняя ожидаемая доходность, ожидаемый риск, среднеквадратическое отклонение). Тогда для пакета активов
(средняя ожидаемая доходность, ожидаемый риск, среднеквадратическое отклонение). Тогда для пакета активов 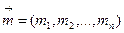
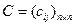
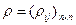
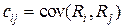 - коэффициент ковариации случайных величин
- коэффициент ковариации случайных величин  ,
,  - коэффициент корреляции случайных величин
- коэффициент корреляции случайных величин  . По диагонали в матрице ковариации стоят дисперсии, а в матрице корреляции 1.
. По диагонали в матрице ковариации стоят дисперсии, а в матрице корреляции 1. и его матрицу ковариации
и его матрицу ковариации  (корреляции
(корреляции  - PEPSI, а
- PEPSI, а  - MOBIL. Воспользуемся результатами примера 3.1. Средняя ожидаемая доходность акции PEPSI- 2.651, а акции - 0.731. Значит
- MOBIL. Воспользуемся результатами примера 3.1. Средняя ожидаемая доходность акции PEPSI- 2.651, а акции - 0.731. Значит  . Поэтому вектор средних -
. Поэтому вектор средних -  . Дисперсия для первого актива - 6.7979, для второго - 8.737769,
. Дисперсия для первого актива - 6.7979, для второго - 8.737769, .
.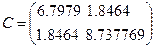 .
.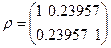 .
.